Đề ôn tập thi vào lớp 10 môn Toán - Số 5

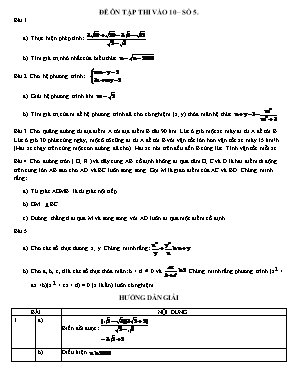
ĐỀ ÔN TẬP THI VÀO 10 – SỐ 5.
Bài 1. 
Thực hiện phép tính: .
Tìm giá trị nhỏ nhất của biểu thức .
Bài 2. Cho hệ phương trình:
Giải hệ phương trình khi .
Tìm giá trị của m để hệ phương trình đã cho có nghiệm (x; y) thỏa mãn hệ thức .
Bài 3. Cho quãng đường từ địa điểm A tới địa điểm B dài 90 km. Lúc 6 giờ một xe máy đi từ A để tới B Lúc 6 giờ 30 phút cùng ngày, một ô tô cũng đi từ A để tới B với vận tốc lớn hơn vận tốc xe máy 15 km/h (Hai xe chạy trên cùng một con đường đã cho). Hai xe nói trên đều đến B cùng lúc. Tính vận tốc mỗi xe.
Bài 4. Cho đường tròn ( O; R ) và dây cung AB cố định không đi qua tâm O; C và D là hai điểm di động trên cung lớn AB sao cho AD và BC luôn song song. Gọi M là giao điểm của AC và BD. Chứng minh rằng:
Tứ giác AOMB là tứ giác nội tiếp.
OM BC.
Đường thẳng d đi qua M và song song với AD luôn đi qua một điểm cố định.
Bài 5. 
Cho các số thực dương x; y. Chứng minh rằng:.
Cho a, b, c, d là các số thực thỏa mãn: b + d 0 và . Chứng minh rằng phương trình (x2 + ax +b)(x2 + cx + d) = 0 (x là ẩn) luôn có nghiệm.
HƯỚNG DẪN GIẢI
BÀI
NỘI DUNG
1
a)
Biến đổi được:
b)
Điều kiện 
Dấu “ = “ xảy ra khi (thỏa mãn). Vậy giá trị nhỏ nhất cần tìm là .
2
a)
Khi m = ta có hệ phương trình 
b)
 Giải tìm được: 
Thay vào hệ thức ; ta được 
Giải tìm được 
3
Xe máy đi trước ô tô thời gian là : 6 giờ 30 phút - 6 giờ = 30 phút = .
Gọi vận tốc của xe máy là x ( km/h ) ( x > 0 )
Vì vận tốc ô tô lớn hơn vận tốc xe máy 15 km/h nên vận tốc của ô tô là x + 15 (km/h)
Thời gian xe máy đi hết quãng đường AB là : 
Thời gian ô tô đi hết quãng đường AB là : 
Do xe máy đi trước ô tô giờ và hai xe đều tới B cùng một lúc nên ta có phương trình : 
Ta có : 
 ( không thỏa mãn điều kiện )
 ( thỏa mãn điều kiện )
Vậy vận tốc của xe máy là 45 ( km/h ) , vận tốc của ô tô là 45 + 15 = 60 ( km/h ).
4
Hình vẽ
a)
Chứng minh được: 
-hai cung AB và CD bằng nhau
- sđ góc AMB bằng sđ cung AB
 Suy ra được hai góc AOB và AMB bằng nhau
 O và M cùng phía với AB. Do đó tứ giác AOMB nội tiếp 
b)
Chứng minh được: 
- O nằm trên đường trung trực của BC (1)
- M nằm trên đường trung trực của BC (2)
 Từ (1) và (2) suy ra OM là đường trung trực của BC, suy ra 
c)
Từ giả thiết suy ra 
Gọi I là giao điểm của đường thẳng d với đường tròn ngoại tiếp tứ giác AOMB, suy ra góc OMI bằng , do đó OI là đường kính của đường tròn này
Khi C và D di động thỏa mãn đề bài thì A, O, B cố định, nên đường tròn ngoại tiếp tứ giác AOMB cố định, suy ra I cố định. 
Vậy d luôn đi qua điểm I cố định.
5
a)
a) Với x và y đều dương, ta có (1)
 (2)
(2) luôn đúng với mọi x > 0, y > 0. Vậy (1) luôn đúng với mọi 
b)
Xét 2 phương trình: x2 + ax + b = 0 (1) và x2 + cx + d = 0 (2)
+ Với b+d <0 b; d có ít nhất một số nhỏ hơn 0 
 >0 hoặc >0 pt đã cho có nghiệm
+ Với . Từ ac > 2(b + d) => 
=> Ít nhất một trong hai biểu giá trị => Ít nhất một trong hai pt (1) và (2) có nghiệm.
Vậy với a, b, c, d là các số thực thỏa mãn: b + d 0 và ,
phương trình (x2 + ax +b)(x2 + cx + d)=0 (x là ẩn) luôn có nghiệm.