Ôn tập môn hình học lớp 8 - Định lí talet - Phân giác – tam giác đồng dạng

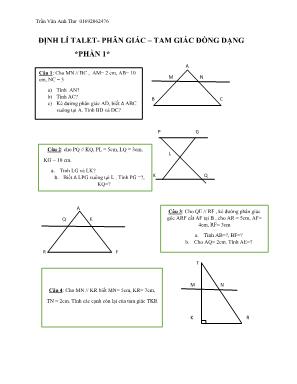
Trần Văn Anh Thư 01692062476 
 ĐỊNH LÍ TALET- PHÂN GIÁC – TAM GIÁC ĐỒNG DẠNG 
 *PHẦN 1* 
 A 
 M N 
 B C 
 P G 
 L 
 K Q 
 A 
 Q E 
 R F 
 T 
 M N 
 K R 
Câu 1: Cho MN // BC , AM= 2 cm, AB= 10 
cm, NC = 3 
a) Tính AN? 
b) Tính AC? 
c) Kẻ đường phân giác AD, biết ∆ ABC 
vuông tại A. Tính BD và DC? 
Câu 2: cho PQ // KQ, PL = 5cm, LQ = 3cm, 
 KG = 10 cm. 
a. Tính LG và LK? 
b. Biết ∆ LPG vuông tại L . Tính PG =?, 
KQ=? 
Câu 3: Cho QE // RF , kẻ đường phân giác 
góc ARF cắt AF tại B , cho AR = 5cm, AF= 
4cm, RF= 3cm 
a. Tính AB=?, BF=? 
b. Cho AQ= 2cm. Tính AE=? 
Câu 4: Cho MN // KR biết MN= 5cm, KR= 7cm, 
TN = 2cm. Tính các cạnh còn lại của tam giác TKR 
Trần Văn Anh Thư 01692062476 
 * PHẦN 2* 
Câu 5: Cho ∆ABC vuông tại A,đường cao AH, phân giác AD, AB= 3 cm, AC= 4cm 
a. Tính BC=? 
b. Chứng minh:∆𝐴𝐵𝐻~∆𝐴𝐵𝐶 
c. CMR: AB2 = BH.BC 
d. Chứng minh: ∆𝐴𝐶𝐻~∆𝐴𝐵𝐶 
e. CMR: AC2= CH.BC 
f. Chứng minh:∆𝐴𝐵𝐻~∆𝐴𝐻𝐶 
g. Tính BH=? Và CH=? 
Câu 6: Cho tam giác ABC vuông tại A có đường cao AH. Gọi D và E lần lượt là hình chiếu 
vuông góc của H lên AB và AC. 
a) Chứng minh: ΔABC đồng dạng ΔHBA. 
b) Chứng minh: AH2 = HB.HC. 
c) Cho HB = 4cm, HC = 9cm. Hãy tính DE. 
Câu 7: Cho ΔKPQ vuông tại K có KH là đường cao. 
a) Chứng minh ΔKPQ đồng dạng ΔKHQ. 
 Từ đó suy ra KQ2 = QH.PQ. 
 b) Tính KQ, KH, HQ biết KP = 9cm, PQ = 15cm. 
 c) Chứng minh: KH2 = HP.HQ.