Kì thi học sinh giỏi môn thi: Vật lý. Lớp 12 thpt thời gian: 180 phút (không kể thời gian giao đề thi)

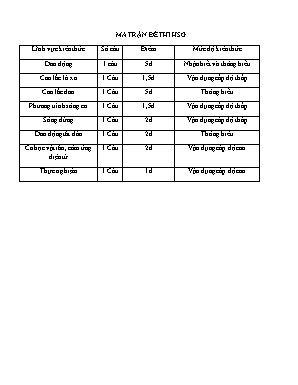
MA TRẬN ĐỀ THI HSG
Lĩnh vực kiến thức
Số câu
Điểm
Mức độ kiến thức
Dao động
1 câu
5đ
Nhận biết và thông hiểu
Con lắc lò xo
1 Câu
1,5đ
Vận dụng cấp độ thấp
Con lắc đơn
1 Câu
5đ
Thông hiểu
Phương trình sóng cơ
1 Câu
1,5đ
Vận dụng cấp độ thấp
Sóng dừng
1 Câu
2đ
Vận dụng cấp độ thấp
Dao động tắt dần
1 Câu
2đ
Thông hiểu
Cơ học vật rắn, cảm ứng điện từ
1 Câu
2đ
Vận dụng cấp độ cao
Thực nghiệm
1 Câu
1đ
Vận dụng cấp độ cao
TRƯỜNG THPT HẬU LỘC 4
Tổ: Vật lí-KTCN
KÌ THI HỌC SINH GIỎI 
Môn thi: Vật lý. Lớp 12. THPT
Thời gian: 180 phút (không kể thời gian giao đề thi)
Đề thi này có 8 câu, gồm 02 trang.
Câu 1(5đ): Một chất điểm m dao động điều hòa theo phương trình x=10cos(20πt+π/3) cm
 a.Tìm vận tốc cực đại? gia tốc cực đại?
 b.Tìm gia tốc và vận tốc tại vị trí vật có li độ 5cm?
 c.Tìm vận tốc và gia tốc tại thời điểm t=1/60 (s)?
 d.Tìm tốc độ trung bình khi vật đi từ x=-5cm theo chiều dương đến x=5 cm lần 1?
 e. Tìm thời điểm vật có li độ 5cm lần thứ 235 kể từ t0=4s?
Câu 2(5đ): Một con lắc đơn có chiều dài 160cm treo tại nơi có g=10 m/s2. Chất điểm có khối lượng 500g. Mốc thế năng ở VTCB. Kéo con lắc lệch khỏi VTCB góc 0,05 rad về phía âm của trục tọa độ rồi truyền cho vật tốc độ 20cm/s vuông góc với dây và hướng về vị trí cân bằng của vật. Trục tọa độ trùng với quỹ đạo của vật, gốc ở VTCB, mốc thời gian là lúc truyền vận tốc. Mốc thế năng ở VTCB.
 a.Viết phương trình li độ góc?
 b.Tìm động năng tại vị trí dây treo tạo với phương đứng góc 0,04rad?
 c.Tìm li độ góc khi động năng bằng 3 lần thế năng?
 d. Tìm lực căng dây khi dây treo tạo với phương đứng góc 0,05rad?
 e. Tìm gia tốc của vật khi dây treo tạo với phương đứng góc 0,05 rad?
Câu 3(1,5đ): Một con lắc lò xo treo thẳng đứng, kéo vật xuống dưới VTCB 1,5cm rồi truyền cho vật tốc độ 30 cm/s thẳng đứng hướng lên. Khi vật ở vì trí có độ cao cực tiểu thì lò xo dãn 8cm. g=10 m/s2. Tìm vận tốc cực đại của vật?
Câu 4(1,5đ): Một sóng ngang lan truyền trên dây đàn hồi rất dài căng dọc theo trục ox theo chiều từ O đến M với tốc độ truyền sóng là 10m/s. Điểm M trên dây cách O 0,5π (m), coi biên độ sóng không đổi. Phương trình uO=0,025cos(10t+π/6) (m). t tính bằng s. Bỏ qua mọi mất mát năng lượng. Tìm hệ số góc của tiếp tuyến tại điểm M ở thời điểm t=0,025π s? 
Câu 5(2đ): Một đồng hồ con lắc được coi như con lắc đơn dao động tại nơi có g=π2m/s2. Biên độ dao động lúc đầu của con lắc là 50. Do chịu lực cản không đổi là 0,012(N) nên nó dao động tắt dần với chu kì 2s. Để duy trì dao động cho con lắc người ta dùng một pin có E=3V, r=0Ω với hiệu suất 25%. Biết cứ 90 ngày phải thay pin mới. Tìm điện lượng ban đầu của pin nếu:
Năng lượng được bổ sung một cách liên tục? 
Năng lượng được bổ sung sau mỗi chu kì dao dao động và vật có khối lượng 500g?
Câu 6(2đ): Một thanh kim loại mảnh OA dài 2m, đồng chất phân bố đều có thể quay quanh quanh trục nằm ngang đi qua O. Gia tốc trọng trường là g=10 m/s2. Kéo thanh lệch khỏi VTCB góc 100 rồi thả không vận tốc. Thanh được đặt trong từ trường đều có véc tơ cảm ứng từ vuông góc với mặt phẳng dao động của thanh và có độ lớn B=0,1T. Hai đầu thanh để hở và cách điện. Bỏ qua mọi ma sát và lực cản của môi trường và hao phí do dòng phuco. Tìm suất điện động hai đầu thanh khi thanh tạo với phương đứng góc 50? Tìm suất điện động cực đại giữa hai đầu thanh? 
Câu 7(2đ): Người ta sử dụng một nam châm điện có tần số của dòng điện xoay chiều chạy qua nam châm là 10Hz để tạo sóng dừng trên một sợi dây kim loại mảnh. Trên dây xuất hiện sóng dừng. Gọi thứ tự các điểm thuộc dây lần lượt là O,M,N,P sao cho O là điểm nút, P là điểm bụng sóng gần O nhất (M,N thuộc đoạn OP) . Khoảng thời gian ngắn nhất giữa 2 lần liên tiếp để li độ của điểm P bằng biên độ dao động của điểm M là 1/60 s và thời gian ngắn nhất hai lần liên tiếp li độ P bằng biên độ N là 1/120 s. Biết khoảng cách từ vị trí cân bằng của M đến vị trí cân bằng của N là 0,2cm. Tìm Khoảng cách giữa hai nút sóng liên tiếp trên dây và vận tốc truyền sóng?
Câu 8 (1đ). Hai quả cầu, một bằng đồng, một bằng nhôm khối lượng bằng nhau. Quả cầu bằng đồng có phần rỗng hình cầu, đồng tâm với quả cầu. Hình dạng, kích thước bên ngoài hai quả cầu giống hệt nhau. Chỉ với một tấm bìa phẳng, cứng, nhám, hãy trình bày phương án thí nghiệm để phân biệt hai quả cầu trên. Viết các công thức cần thiết để giải thích phương án thí nghiệm?
..HẾT..
ĐÁP ÁN ĐỀ THI HỌC SINH GIỎI VẬT LÍ NĂM 2015-2016
Câu1
Cách giải
Điểm
 1a 
vmax=Aω=200π cm/s; amax=4000π2 cm/s2
1đ
 1b
a=-ω2x=2000π2 cm/s2 , v=±ω=±100π cm/s
1đ
 1c
v=-200πsin(20π.1/60+π/3)=-100π cm/s
a=-10.(20π)2cos(20π.1/60+π/3)=2000π2 cm/s2.
1đ
1d
Vẽ vòng tròn tính được Δφ=π/2Δt=Δφ/ω=1/40s
0,5đ
Vtb=s/t=40.(5+5)
0,5đ
1e
t235=t1+117T=4+3/40+11,7=15,775 s
1đ
Câu2
2a
α=0,1cos(2,5t-5π/6) rad 
1đ
2b
Eđ=0,5mgl(=0,03J
1đ
2c
4Et=Eα=±0,05 rad
1đ
2d
T=mg(=5,03125 (N)
1đ
2e
a==g.=0,70887 m/s2
gia tốc tạo với dây góc β mà tanβ=at/anβ=0,14 rad
1đ
Câu 3
A=0,08-Δlcb=0,08-10/ω2
0,25đ
A2=(0,08-10/ω2)2=x2+v2/ω2 tính được ω=10 rad/s và A=3cm
1đ
Vmax=Aω=30 cm/s
0,25đ
Câu 4
u=Acos(10t+π/6-2πx/λ)
0,5đ
k=u’x=0,025.(2π/λ).sin(10t+π/6-2πx/λ)=-0,065
1đ
Câu 5
5a
l=g.T2/(4π2)=1m
qEH=FC.4lα0t/Tq=4Fclα0t/(EHT)=21714,69 (C)
1đ
5b
Tính được độ giảm biên độ sau 1T là: Δα=4FC/P 
0,25đ
qEH=0,5mglt/T
0,5đ
q=0,5mglt/(EHT)= 20504,5 C (20252,72)
0,25đ
Câu 6
-0,5mglα=Iα’’α’’=-(0,5mgl/I)α=-(3g/2l)α=-ω2α
α=α0cos(ωt+φ) ; ω=
0,25đ
e=-Δϕ/Δt=-ϕ’=-(B.l2α/2)’=0,5Bl2ωα0sin(ωt+φ)
1đ
α=±50=10cos(ωt+φ)ccos(ωt+φ)=±0,5sin(ωt+φ)=±/2
e=0,5.0,1.22..(10π/180).( ±/2)=0,08279 V
0,5đ
emax=0,5 Bl2ωα0=0,0956V
0,25đ
Câu 7
Lập được cộng thức sóng dừng của điểm B cách bụng P một khoảng d suy ra biên độ AB =
0,25đ
f=2fđ=20Hz, ω=2πf=40π rad/s
Δφ1=ω.Δt1=2π/3 rad, cos(Δφ1/2)=AM/APcos(2πdM/λ) suy ra dM=λ/6
Δφ2=ω.Δt2=π/3 rad, cos(Δφ1/2)=AN/APcos(2πdN/λ) suy ra dN=λ/12
1đ
MN=λ/6-λ/12=0,2 suy ra λ=2,4 cm
Khoảng cách giữa hai nút sóng liên tiếp là λ/2=1,2 cm, v=λ.f=48 cm/s
0,75
Câu 8
-Dùng tấm bìa làm mặt phẳng nghiêng với góc nghiêng nhỏ (để các quả cầu lăn không trượt)
0,25đ
-Thả đồng thời hai quả cầu, quả nào lăn xuống trước là quả cầu nhôm
0,25đ
Giải thích: Vận tốc của quả cầu khi xuống tới chân mặt phẳng nghiêng được tính theo định luật bảo toàn cơ năng:
Vì mômen quán tính nên , do đó . Tức là tốc độ trung bình của quả cầu nhôm lớn hơn tốc độ trung bình quả cầu đồng.
0,5đ
A.-0,00647 B. -0,00325 C. 0,00325 D. 0,00647
 A. 5,6cm B. 4,8 cm C. 1,2cm D. 2,4cm
 A.200µC B. 10875C C. 10861C D. 104C
------------------ HẾT ------------------
- Thí sinh không sử dụng tài liệu.
- Giám thị coi thi không giải thích gì thêm
ĐÁP ÁN CHẤM ĐỀ THI HỌC SINH GIỎI 2013-014
Câu 1(3đ):
a(1đ) . γ= (rad/s2) 0,5đ
 ω=ω0+γt1 =16 (rad/s2) 0,5đ 
b(1đ). ω=ω0+γt=0 t=-ω0/γ=20 (s) 1đ
c(1đ). (rad/s2) 0,75đ
 ωtb= 13(rad/s2) 0,25đ
Câu 2(4đ): 
a(2đ). vmax=Aω, amax= A.ω2 ω= amax/vmax =4π(rad/s);A= vmax/A=10 cm 1,25đ 
 Tìm được φ=-π/2 (rad) 0,5đ 
 x=Acos(ωt+φ) =10cos(4πt-π/2) (cm) 0,25π
b(1π). Vẽ được mối liên hệ giữa chuyển động tròn và dao động điều hòa 0,25đ
 =5π/6 rad 0,5đ
 t= /ω=1/12 s 0,25đ
c(1đ). Tính được == (m) 0,5đ
 Fđh=K(+x)=6,25+10cos(4πt-π/2) 0,5đ
Câu 3(3đ):
a(2đ). λ=v/f=10 cm 0,5đ
 u1M=Acos(ωt+φ1-2πd1/λ) 0,25đ 
 u2M=Acos(ωt+φ2-2πd2/λ) 0,25đ 
 uM=u1M+u2M= 2Acos 0,5đ
 = 8cos cos(40πt-83π/15) 0,5đ
b(1đ). Tìm được vị trí cực đại d2-d1=10k+5/3 (cm) với kZ. 0,5đ
 -44≤10k+5/3≤44 -4,57≤k≤4,23có 9 giá trị kZ nên có 9 điểm cực đại 0,5đ
Câu 4(3đ):
a) L-L0=20lg(r0/r) 1đ
 r0=10r=1000 (m) 0,5đ
b) Vị trí các nút x=4k (k Z) 0,5đ
 /2=xk+1-xk=4 λ=8 cm 0,25đ
V=λ.f=80 cm/s 0,25đ
 Tìm được vị trí điểm M có AM=1 cm: x=2+4k (kZ) 0,5đ
Câu 5:
T
F
P
a
 x
+ Gia tốc chuyển động xuống dốc của xe là a = gsina. 0,25đ 
Xét hệ quy chiếu gắn với xe 
Tại vị trí cân bằng 
 Ta có: 0,25đ
+ Chiếu phương trình trên xuống phương OX song song với mặt dốc ta có: Psina - F + TX = 0
Mà F = ma = mgsina 
suy ra TX = 0. 
Điều này chứng tỏ ở vị trí cân bằng dây treo con lắc vuông góc với Ox 0,5đ
+ Vị trí cân bằng như trên thì trọng lực biểu kiến của con lắc là P' = Pcosa. Tức là gia tốc biểu kiến là g' = gcosa. 0,5đ
+ Vậy chu kì dao động của con lắc sẽ là T = 2p = 2p » 2,83 (s). 0,5đ
Câu 6(2đ):
Vẽ được GĐVT 0,5đ
 1đ
A2max=10cm khi α=π/2 φ=-π/6 rad 0,5đ
Câu 7(1,5đ):
 -Pt.Lα/4-Pm.3L/4=Ihα” 0,5đ
α”=-=-ω2.α vật dao động điều hòa 0,25đ
Chu kì dao động: T=2π. 0,25đ
(Im+It).ω=Im.V/(3L/4) 0,25đ
 ω=18V/L 0,25đ 
Câu 8(1,5đ):
 a(1đ). Ta có:	
* Chiếu lên phương tiếp tuyến:	 
	(0,25đ)
	Với:	ω2=g/R	(0,25đ)
Từ đó cho thấy m dao động điều hoà, thời gian đi từ A đến B là 1/2 chu kỳ dao động.
	 0,25đ	(0,25đ)
B(0,5đ). Chén đứng yên nên:	(1)
* Chiếu (1) lên phương Oy:	Với N' = N	(2)	
Ở góc lệch a, Với m có:	(3)	0,25đ
Từ (2) và (3) ta được:	(4)	
m
I
M
A
NM
Fmsn
PMM
N'
N
O
O
y
x
a
* Chiếu (1) lên Ox:	
	a0 bé; a £ a0 	
	 khi a = a0 	 (0,25đ)
Vậy:	 (0,25đ)
Câu 3:( 5 điểm). Một cái đĩa nằm ngang, có khối lượng M= 200 g, được gắn vào đầu trên của một lò xo thẳng đứng có độ cứng k= 20 N/m. Đầu dưới của lò xo được giữ cố định. Đĩa có thể chuyển động theo phương thẳng đứng. Bỏ qua mọi ma sát và lực cản của không khí. cho gia tốc trong trường g =10 m/s2.
1.Ban đầu đĩa ở vị trí cân bằng. Ấn địa xuống một đoạn 5 cm, rồi thả cho đĩa tự do. Lấy trục toạ độ Ox theo phương thẳng đứng, gốc O trùng với vị trí cân bằng, chiều dương hướng từ trên xuống, gốc thời gian là lúc thả đĩa. Viết phương trình dao động của đĩa?
2.Đĩa đang nằm ở vị trí cân bằng, người ta thả một vật có khối lượng m=100 g rơi tự do từ độ cao h = 80 m so với mặt đĩa. Va chạm giữa vật và mặt đĩa là hoàn toàn đàn hồi. Sau va chạm đầu tiên, vật nảy lên và được giữ lại không cho rơi xuống đĩa nữa.
a.Tính vận tốc của đĩa ngay sau khi va chạm vào vật ? 
b.Tính tần số góc và biên độ dao động A’ của đĩa?
c.Viết phương trình dao động của đĩa. Lấy mốc thời gian là lúc vật chạm vào đĩa, trục toạ độ, gốc toạ độ như trên.
1.Phương trình dao động có dạng : x = A cos( t + ) cm
Trong đó: A= 5 cm;= 10 rad/s = 0 rad.
Vậy : x = 5 cos( 10 t) cm
2.a) Tính vận tốc của đĩa ngay sau khi va chạm.
Vận tốc của vật m trước khi va chạm vào đĩa: v = = 40 m/s
Coi hệ va chạm là hệ kín nên áp dụng định luật bảo toàn động lượng ta có:
mv=mv1+Mv2 (1)
Vì va chạm là đàn hồi xuyên tâm nên động năng được bảo toàn:
=+(2)
Từ (1) và (2) ta tìm được vận tốc của đĩa sau khi va cham: v2 = = 80/3= 26,667 m/s.
b.Tính tần só góc và biên độ dao động A’ của đĩa.
* = = 10 rad/s
* Áp dụng định luật bảo toàn năng lượng:
= suy ra 
A’ = v2= 80/30=8/3 cm
c.Viết phương trình dao động của đĩa
x= A’ cos(t + ) cm
Với: A’ = 8/3 cm; = 10 rad/s
 Căn cứ vào trục toạ độ và mốc thời gian tìm được: = - rad
Vậy phương trình dao động của đĩa: x = cos( 10t-) cm
0,5 đ
0,5 đ
0,5 đ
0,5 đ
0,5 đ
0,5 đ
0,25 đ
0,5 đ
0,25 đ
0,5 đ
0,25 đ
0,25 đ
m
I
M
A
NM
Fmsn
PM
N'
N
O
O
y
x
a
Bài 4: (Dao động điều hòa - 3 điểm)
Từ điểm A trong lòng một cái chén tròn M đặt trên mặt sàn phẳng nằm ngang, người ta thả một vật m nhỏ (hình vẽ). Vật m chuyển động trong mặt phẳng thẳng đứng, đến B thì quay lại. Bỏ qua ma sát giữa chén M và m.
a. Tìm thời gian để m chuyển động từ A đến B. Biết A ở cách điểm giữa I của chén một khoảng rất ngắn so với bán kính R. Chén đứng yên.
b. Tính hệ số ma sát nghỉ giữa chén và sàn.
Giải
m
V
B
A
O
·
H×nh 5
Bµi 4: (4,5 ®iÓm) Mét thanh cøng AB ®ång chÊt, dµi L, khèi l­îng M cã thÓ quay kh«ng ma s¸t trong mÆt ph¼ng th¼ng ®øng quanh mét trôc cè ®Þnh n»m ngang ®i qua ®iÓm O trªn thanh víi OA=L/4. Ban ®Çu thanh ®ang ®øng yªn th¼ng ®øng th× mét vËt nhá cã khèi l­îng m=M/3 bay theo ph­¬ng ngang tíi va ch¹m vµo ®Çu B cña thanh víi vËn tèc V (h×nh 5). Sau va ch¹m, vËt dÝnh vµo thanh vµ hÖ thanh - vËt b¾t ®Çu dao ®éng víi gãc lÖch bÐ xung quanh vÞ trÝ c©n b»ng. Chøng tá r»ng dao ®éng cña hÖ thanh - vËt lµ dao ®éng ®iÒu hoµ. LËp c«ng thøc tÝnh chu k× dao ®éng vµ viÕt ph­¬ng tr×nh dao ®éng.
A2max? A.- p/3; 8cm B.-p /6;10cm 	 C. p/6; 10cm 	 D. B hoặc C