Đề thi giải toán trên máy tính cầm tay môn: Toán lớp 9 thời gian: 150 phút (không kể phát đề)

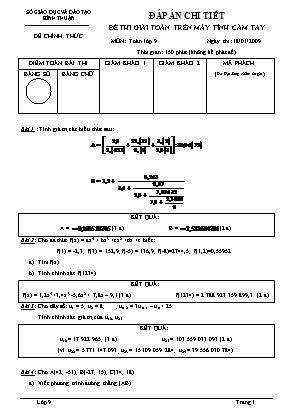
SỞ GIÁO DỤC VÀ ĐÀO TẠO
BÌNH THUẬN
--------------------------------
ĐỀ CHÍNH THỨC
ĐÁP ÁN CHI TIẾT 
 ĐỀ THI GIẢI TOÁN TRÊN MÁY TÍNH CẦM TAY
MÔN: Toán lớp 9 Ngày thi: 18/01/2009
Thời gian: 150 phút (không kể phát đề)
ĐIỂM TOÀN BÀI THI
GIÁM KHẢO 1
GIÁM KHẢO 2
MÃ PHÁCH
(Do Hội đồng chấm thi ghi)
BẰNG SỐ
BẰNG CHỮ
Bài 1 : Tính giá trị các biểu thức sau:
KẾT QUẢ:
A = (3 đ) B = (2 đ)
Bài 2: Cho đa thức f(x) = ax4 + bx3 +cx2 +dx +e biết:
	 f(1) = -2,3; f(3) = 152,9; f(-5) = 136,9; f(-8)=2744,5; f(1,2)=0,55952.
Tìm f(x).
Tính chính xác f(1234).	
KẾT QUẢ:
f(x) = 1,2x4 +3,4x3 -5,6x2 + 7,8x – 9,1 (3 đ) f(1234) = 2 788 923 359 899,3 (2 đ)
Bài 3: Cho dãy số: u1 = 5; u2 = 8; . . . ; un+2 = 3un+1 – un + 25
	Tính chính xác giá trị của u16; u25. 	 
	KẾT QUẢ:
u16 = 17 922 965; (3 đ) u25 = 103 559 033 093 (2 đ)
(vì u22 = 5 771 147 093, u23 = 15 109 059 284; u24 = 39 556 030 784) 
Bài 4: Cho A(42; -51); B(-27; 15); C(34; 18)
Viết phương trình đường thẳng (AB).	
Tính số đo góc ABC? 	
Tính độ dài đường phân giác trong AD của tam giác ABC.	
KẾT QUẢ:
Phương trình đường thẳng (AB):	 (2 đ)
 b) (1,5 đ) c) (1,5 đ)
Bài 5: Giải các phương trình và hệ phương trình sau:
a) b) 
CÁCH GIẢI : 
a) (2 đ) 
b) (2 đ) * (x=0; y=0) là nghiệm của hệ.
 * Khi x ≠ 0, (2) Û xy2 + x3y + 2x2 = 0 (2’) 
	 (2’) - (1) được: 
 Thay vào (1) ta được : 3x6 + 11x3 + 8 = 0
Vậy nghiệm của hệ (x=0; y=0); (x=-1; y=1); 
 (x= -1,386722546; y=-2,884499141);
KẾT QUẢ
a) (0,5 đ)
b) Vậy nghiệm của hệ: 
(x=0; y=0); 
 (x=-1; y=1); 
(x= -1,386722546; 
 y = -2,884499141); (0,5 đ)
Bài 6: a) Tìm hai chữ số tận cùng của tổng 2999 + 39999.
 b)Tìm chữ số thập phân thứ 2009 của .
	KẾT QUẢ:
a) Ta có: 	
nên 2999 + 39999 
Vậy hai chữ số tận cùng của 2999 + 39999 là 55.
b) 	chu kì là 22
	Mà 2009: 22 dư 7
	Vậy chữ số thập phân thứ 2009 là 6.
Bài 7: Cho tam giác ABC, lấy điểm D thuộc cạnh AB sao cho . Trên cạnh AC lấy điểm E sao cho . Gọi F là giao điểm của BE và CD. Biết AB = 7,26cm; AF = 4,37cm; BF=6,17cm.
a) Tính diện tích tam giác ABF.
b) Tính diện tích tam giác ABC.
KẾT QUẢ:
	a) SABF = 13,43529949 cm2.
	b) Đặt SABF = 4SBDF = 4x; SACF = 5SCEF = 5y
	SABF +SAEF = 4x + 4y =SABC ; 
 SADF +SACF = 3x + 5y =SABC 
	 Ta có hệ:
	Þ SABC = 8x Þ SABC = 2SABF = 26,87059898 cm2.
Bài 8: Cho đoạn OO’ = 55,66 cm, vẽ (O; 33,44cm) và (O’; 11,22cm). Gọi EF là tiếp tuyến chung trong của hai đường tròn (EÎ(O), FÎ(O’)). Đường thẳng OO’ cắt đường (O) tại A, B và cắt (O’) tại C, D (B, C nằm giữa A và D). Gọi M, N, I lần lượt là giao điểm của AE và CF, BE và DF, MN và AD.
a) Tính phần diện tích S của hình tròn có đường kính là AD ở ngoài hai đường tròn (O) và (O’).
b) Tính độ dài đoạn AI?
CÁCH GIẢI câu b: 
a) S=11271,906 cm2.
b) Ta có: OE // O’F (cùng vuông góc với EF) 
Þ Ô1=Ô’1 Þ ÐA=ÐD Þ AM//DN 
Þ MENF là hình chữ nhật
 (3 đ) 
KẾT QUẢ
a) S = 3 995,803006 cm2.
b) IA = 
 = 70,18434783 cm (1 đ) 
Bài 9: Thể tích của một khối vàng đặc nguyên chất hình lập phương là một số tự nhiên có ba chữ số cm3. Biết độ dài của cạnh là x+y+z cm.
a) Tính cạnh và thể tích của khối vàng?
b) Biết khối lượng riêng của vàng là 19300kg/m3 và giá một chỉ vàng (1 chỉ = 3,78g) là 1750000 đồng. Hỏi nếu bán khối vàng này thì được bao nhiêu tiền?
CÁCH GIẢI : 
a) Ta có 99<<1000 Þ 99<(x+y+z)3<1000 Þ 4<x+y+z<10
	Nếu x+y+z =5 thì = 53 = 125 (loại vì 1+2+5 ≠5)
	Nếu x+y+z =6 thì = 63 = 216 (loại vì 2+1+6 ≠6)
	Nếu x+y+z =7 thì = 73 = 343 (loại vì 3+4+3 ≠7)
	Nếu x+y+z =8 thì = 83 = 512 (chọn vì 5+1+2 =8)
	Nếu x+y+z =9 thì = 93 = 729 (loại vì 7+2+9 ≠9)
Vậy thể tích của khối vàng là 512 cm3; cạnh là 8 cm. (2 đ) 
b) Khối lượng vàng: 512 . 19,3 = 9881,6 (g)
	Số chỉ vàng: 9881,6:3,78 = 494080/189 = 2614,179894 (chỉ)
	Số tiền thu về khi bán khối vàng trên là:
494080/189 . 1750000 = 4574814814,8 (đồng) (1 đ) 
KẾT QUẢ
a) Thể tích của khối vàng là 
512 cm3; cạnh là 8 cm. (1 đ)
b) Số tiền:
4574814814,8 (đồng) (1 đ)
Bài 10: Tìm giá trị lớn nhất và giá trị nhỏ nhất của M = 	
KẾT QUẢ:
Cách 1: M = Û 3,989Mx2 - 7,998x + M-3,001=0 
Có D’ = -3,989M2 + 11,970989M + 15,992001 nên D’³0 Û -1,001604178 £ M £ 4,002604178
Vậy Mmin= -1,001604178 (2,5 đ) ; Mmax= 4,002604178 (2,5 đ) 
Cách 2:
Vậy Mmin= -1,00160 (2,5 đ) 
 Vậy Mmax= 4,00260 (2,5 đ)