Đề ôn tập môn Toán Lớp 11 Đường thẳng vuông góc mặt phẳng

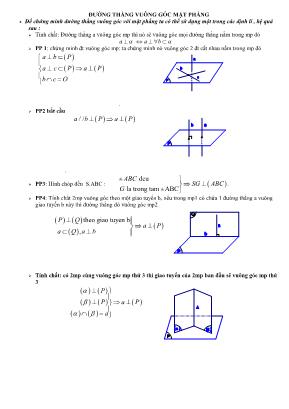
ĐƯỜNG THẲNG VUÔNG GÓC MẶT PHẲNG 
 Để chứng minh đường thẳng vuông góc với mặt phẳng ta có thể sử dụng một trong các định lí , hệ quả 
sau : 
 Tính chất: Đường thẳng a vuông góc mp thì nó sẽ vuông góc mọi đường thẳng nằm trong mp đó 
 a  a b    
 PP 1: chứng minh đt vuông góc mp: ta chứng minh nó vuông góc 2 đt cắt nhau nằm trong mp đó 
 
   
a b P
a c P a P
b c O
 

   
  
 . 
 PP2 bắt cầu 
    / /a b P a P   
 . 
 PP3: Hình chóp đều S.ABC :  
 deu
 la trong tam ABC
ABC
SG ABC
G

 

. 
 PP4: Tính chất 2mp vuông góc theo một giao tuyến b, nếu trong mp1 có chứa 1 đường thẳng a vuông 
giao tuyến b này thì đường thẳng đó vuông góc mp2 
   
 
 
theo giao tuyen b
,
P Q
a P
a Q a b
 
 
  
 Tính chất: có 2mp cùng vuông góc mp thứ 3 thì giao tuyến của 2mp ban đầu sẽ vuông góc mp thứ 
3 
   
   
   
 
P
P a P
a


 
 

  

  
c
a
b
P
P
b a
Q
P
b
a
P
()( )

HAI MẶT PHẢNG VUÔNG GÓC 
 Cách 1: Tính góc giữa hai mặt và góc này bằng 900          0, 90P Q P Q   
 Cách 2: Ta chứng minh trong mp1 có chứa 1 đường thẳng a vuông góc mp2 
 
   
( )
a
a

 

 
 
 
 Cách 3: tính chất song song 
   
   
   
/ /
R Q
P Q
P R
 
 

. 
 Tính góc giữa hai đường thẳng Phương pháp : Có thể sử dụng một trong các cách sau: 
 Cách 1: (theo phương pháp hình học) 
 Lấy điểm O tùy ý (ta có thể lấy O thuộc một trong hai đường thẳng) qua đó vẽ các đường thẳng lần 
lượt song song (hoặc trùng) với hai đường thẳng đã cho 
 Tính một góc trong các góc được tạo bởi giữa hai đường thẳng cắt nhau tại O . 
 Nếu góc đó nhọn thì đó là góc cần tìm , nếu góc đó tù thì góc cần tính là góc bù với góc đã tính . 
 Cách 2 : (theo phương pháp véc tơ) 
 Tìm 1 2,u u lần lượt là các vectơ chỉ phương của hai đường thẳng    1 2àv  
 Khi đó     1 21 2 1 2
1 2
cos , cos ,
u u
u u
u u

   

. 
 Tính góc giữa đường thẳng và mặt phẳng 
 Phương pháp : 
 Nếu      0, 90a a    ; 
 Nếu    0
/ /
, 0
a
a
a




  
; 
 
 
 
    , , '
'
a
a a a
a hch a



 
 
 
o Để tìm 'a hch a ta lấy tùy ý điểm M a , dựng  MH  tại H và tìm giao điểm của đường 
thẳng và mặt là A, suy ra   ' ,hch a a AH A a      ,a MAH  
 Xác định góc giữa hai mặt phẳng 
Phương pháp : 


a
b'
a'
B
A
O
b
a
 = 
 Cách 1 : Dùng định nghĩa : 
       , ,P Q a b trong đó : 
 
 
a P
b Q
 

 
 Cách 2: 
 +Tìm giao tuyến d của 2 mp 
 +Trong mp1 tìm đường thẳng q vuông góc gt d 
 +Trong mp2 tìm đường thẳng p vuông góc gt d 
 +Kết luận góc giữa 2mp = góc giữa 2 đường thẳng q và p 
 Cách 3 dùng công thức diện tích Gọi hình H nằm trong mp1, gọi H’ là hcvg của hình H lên mp2, khi đó 
góc giữa 2mp là  , khi đó 'cos chieuH
gocH
S
S
  
 Cách 4 : Dùng hệ quả : 
 
 
   
    ,P
M Q
H hch M P Q MNH
HN m P Q
 

  

   
 . 
 Tính các khoảng cách giữa một điểm và mặt phẳng 
Phương pháp : Để tính khoảng cách từ một điểm đến một mặt phẳng , ta phải đi tìm đoạn vuông góc vẽ từ 
điểm đó đến mặt phẳng , ta hay dùng một trong hai cách sau : 
 Cách 1 : 
 Tìm một mặt phẳng (Q) chứa M và vuông góc với (P) . 
 Xác định    m P Q  . 
 Dựng    MH m P Q   , 
  MH P  
suy ra MH là đoạn cần tìm . 
 Cách 2: Dựng    / /MH d  
o Chú ý : 
 Nếu        / / , ,MA d M d A    . 
 Nếu  MA I 
  
  
,
,
d M IM
d A IA


  
 Khoảng cách từ một đường thẳng đến một mặt phẳng: 
 Khi 
 
 
  , 0
a P
d a P
a P

 

 . 
 Khi  / /a P 
      , ,d a P d A P  với  A P . 
 Khoảng cách từ một mặt phẳng đến một mặt phẳng : 
 Khi 
   
   
    , 0
P Q
d P Q
P Q

 

 . 
R
P
Q
p
q
 Khi    / /P Q 
       , ,d P Q d M Q  
với  A P . 
 Khoảng cách giữa hai đường thẳng 
 Khi 
   
   
    
'
, ' 0
'
d
  
   
  
 . 
 Khi               / / ' , ' , ' ,d d M d N         với    , 'M N    . 
 Khoảng cách giữa hai đường thẳng chéo nhau : 
 Đường vuông góc chung của hai đường thẳng chéo nhau 
  và  ' là đường thẳng  a cắt   ở M và cắt 
 ' ở N đồng thời vuông góc với cả   và  ' . 
 Đoạn MN được gọi là đoạn vuông góc chung của hai đường 
thẳng chéo nhau   và  ' . 
 Khoảng cách giữa hai đường thẳng chéo nhau là độ dài đoạn 
vuông góc chung của hai đườngthẳng đó . 
Phương pháp : 
 Cách 1 : Dựng mặt phẳng (P) chứa đường thẳng a và song song với b .Tính khoảng cách từ b đến 
mp(P) . 
 Cách 2 : Dựng hai mặt phẳng song song và lần lượt chứa hai đường thẳng . Khoảng cách giữa hai mặt 
phẳng đó là khoảng cách cần tìm . 
 Cách 3 : Dựng đoạn vuông góc chung và tính độ dài đoạn đó . 
Cách dựng đoạn vuông góc chung của hai đường thẳng chéo nhau : 
 Cách 1: Khi a b 
 Dựng một    ,mp P b P a  tại H . 
 Trong (P) dựng HK b tại K . 
 Đoạn HK là đoạn vuông góc 
chung của a và b . 
 Cách 2: 
 Dựng    , / /P b P a . 
 Dựng  ' Pa hch a , bằng cách lấy M a 
dựng đoạn  MN  , lúc đó a’ là 
đường thẳng đi qua N và song song a . 
 Gọi 'H a b  , dựng / /HK MN 
HK là đoạn vuông góc chung cần tìm . 
(a)
'
M
N
MỘT SỐ HÌNH VẼ VÀ TÍNH CHẤT 
HÌNH CHÓP CÓ CẠNH BÊN VUÔNG GÓC ĐÁY 
S.ABC có đáy là 
tam giác đều, 
 SA đáy, gọi M, 
N ,P lần lượt là 
trung điểm 
AC,CB,BA 
1. 
 ( )
BC AN
BC SAN
BC SA

 

2. ( )
BM AC
BM SAC
BM SA

 

3. ( )
CP AB
CP SAB
CP SA

 

S.ABC có đáy là 
tam giác vuông 
tại B, SA đáy, 
AH là đường cao 
trong tam giác 
SAB 
1. 
 ( )
BC AB
BC SAB
BC SA

 

2. ( )
AH SB
AH SBC AH SC
AH BC

   

S.ABCD có đáy là 
hình vuông tâm O. 
SA đáy đường 
cao AH, AK trong 
tam giác SAB, 
SAD. 
1. ( )
BC AB
BC SAB BC SB
BC SA

   

2. ( )
CD AD
CD SCD CD SD
CD SA

   

3. ( )
BD AC
BD SAC BD SC
BD SA

   

4. ( )
AH SB
AH SBC AH SC
AH BC

   

5. ( )
AK SD
AK SCD AK SC
AK CD

   

S.ABCD có đáy là 
hình chữ nhật. SA
 đáy đường cao 
AH, AK trong tam 
giác SAB, SAD. 
1. ( )
BC AB
BC SAB BC SB
BC SA

   

2. ( )
CD AD
CD SCD CD SD
CD SA

   

3. 
 khong vuong 
 khong vuong( )
BD AC
BD SAC
BD SA



4. ( )
AH SB
AH SBC AH SC
AH BC

   

5. ( )
AK SD
AK SCD AK SC
AK CD

   

A C
B
S
N
M
P
S
B
CA
H
A
B
D
S
H
C
K
A
B
D
S
H
C
K
S.ABCD có đáy là 
hình thoi tâm O. 
góc ABC = 600. 
SA đáy, M, N 
lần lượt là trung 
điểm AB,AD 
1. ( )
BD AC
BD SAC BD SC
BD SA

   

2. ( )
CM AB
CM SAB CM SB
CM SA

   

3. ( )
CN AD
CN SAD CN SD
CN SA

   

Hình chop 
SABCD có đáy 
ABCD là hình 
thang vuông tại A 
và D, 
AB=2CD=2AD, 
SA  đáy. 
Gọi I là tring điểm 
AB. 
1.AICD là hình vuông, chop S.AICD có tính chất 
của hchop đáy là hình vuông. 
2. 
,
( )
( ) ( )
BC AC BC SC
BC SAC
BC SA SBC SAC
  
   
  
3. 
,
( )
( ) ( )
CI AB CI SB
CI SAB
CI SA SCI SAB
  
   
  
HÌNH CHÓP ĐỀU 
Hình chop tam giác 
đều SABC. M,N lần 
lượt là trung điểm 
BC,BA. 
Vì hình chop đều 
nên đáy là tam giác 
đều có trọng tâm G 
SG  đáy 
1. 
,
( )
( ) ( )
BC AM BC SA
BC SAM
BC SG SBC SAM
  
   
  
2. 
,
( )
( ) ( )
AB CN AB SC
AB SCN
AB SG SAB SNC
  
   
  
3. Góc giữa cạnh bên và mặt đáy bằng nhau=góc 
SCG 
4. Góc giữa mặt bên và mặt đáy bằng nhau = góc 
SMA 
Tứ diện đều là hình 
chop tam giác đều có 
cạnh bên bằng cạnh 
đáy 
Có tính chất của hình chop đều trên 
Hình chop tứ giác 
đều S.ABCD, I,J lần 
lượt là trung điểm 
BC, AD 
Kẻ OH  SB 
Vì hình chop đều 
nên đáy là hình 
vuông tâm O, 
SO  đáy 
1. 
BD
( BD) ( ) ( )
AC
AC S SAC SBD
AC SO

   

2.
IJ
( IJ) ( ) ( IJ)
BC
BC S SBC S
BC SO

   

3. 
OH
( )
SB
SB ACH
SB AC

  

góc giữa 2 mặt 
bên là góc AHC 
4.Góc giữa các cạnh bên và đáy bằng nhau = góc 
SBO 
5. Góc giữa các mặt bên và đáy bằng nhau là góc 
SIO 
HÌNH CHÓP CÓ MẶT BÊN VUÔNG GÓC ĐÁY 
S
B
A
C
M
N
A
D C
B
S
I
G
A C
B
S
MN
G
A C
B
S
MN
O
A
B
D C
S
J
I
H
Cho hình 
chop 
S,ABCD có 
đáy là hình 
vuông và 
tam giác 
SAB cân tại 
S nằm trong 
mặt phẳng 
vuông góc 
đáy. 
1. 
    theo giao tuyen AB
( ), can tai S co trung tuyen SH ( )
cung la duong cao,S
SAB ABCD
Trong SAB SAB SH ABCD
H AB


 
 
2. 
AB
( AB)
( ) ( )
BC BC SB
BC S
BC SH SBC SAB
  
   
  
HÌNH LĂNG TRỤ 
Hình lằng trụ xiên tam 
giác 
Hình lăng trụ đứng tam 
giác 
Hình lăng trụ xiên tứ 
giác 
Hình lăng trụ đứng tứ giác 
B
C
A D
S
H
A B
C
D'
C'
B'
A B
C
D'
C'
B'
A B
D
C
D' C'
B'A'
A B
D
C
D' C'
B'A'