Ôn tập môn Toán lớp 11 - Chương 1: Hàm số lượng giác và phương trình lượng giác

CHƯƠNG I: HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Bài 1. CÁC HÀM SỐ LƯỢNG GIÁC
Kiến thức cơ bản:
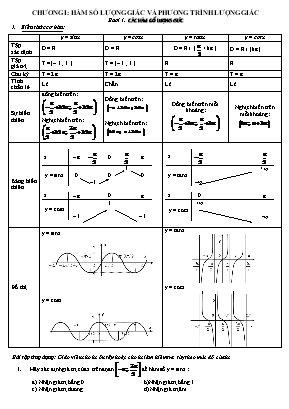
y = sinx
 y = cosx
y = tanx
y = cotx
Tập
xác định
D = R
D = R
D = R \ { + kp}
D = R \ {kp}
Tập
giá trị
T = [– 1 ; 1 ]
T = [– 1 ; 1 ]
R
R
Chu kỳ
T = 2p
T = 2p
T = p
T = p
Tính
chẵn lẻ
Lẻ
Chẵn
Lẻ
Lẻ
Sự biến thiên
đờng biến trên:
Nghịch biến trên:
Đờng biến trên:
Nghịch biến trên:
Đờng biến trên mỡi khoảng:
Nghịch biến trên mỡi khoảng:
Bảng biến thiên
x
–p
0
p
y = sinx
0
–1
0
1
0
x
–p
0
p
y = cosx
– 1
1
– 1
a
x
y = tanx
–¥
+¥
x
0
p
y = cotx
+¥
–¥
a
Đờ thị
y = sinx
y = cosx
y = tanx
y = cotx
Bài tập ứng dụng: Giáo viên cho hs ơn tập hoặc cho hs làm kiểm tra tùy theo mức đợ của hs
Hãy xác định giá trị của x trên đọan để hàm sớ y = sinx :
a)	Nhận giá trị bằng 0.	 	b)Nhận giá trị bằng 1.
c)	Nhận giá trị dương	d) Nhận giá trị âm.
Hãy xác định giá trị của x trên đọan để hàm sớ y = cosx
a) Nhận giá trị bằng 0.	 b) Nhận giá trị bằng -1.
c) Nhận giá trị dương	 d) Nhận giá trị âm.
Tìm tập xác định của mỡi hàm sớ sau:
a)	y = 	b)	y = 	c)	y = 	d)	y = 
e)	y = 	f)	y = 	g)	y = sin3x	h)	y = cos
i)	y = cos	j)	y = sin	k)	y = 	l)	y = m) n) y = tan	o)	y = cos	p)	y = tan q) r) 
Xét tính chẵn, lẻ của mỡi hàm sớ sau:
a)	y = x – sinx b) y = 3sinx – 2 c)y = sinx – cosx d) y = sinxcosx + tanx e) y = f) y = g) y = h) i) y = x3sin2x j) y = tan 
k) y = cos3x l) m)
Tìm giá trị lớn nhất và giá trị nhỏ nhất của mỡi hàm sớ sau:
Chú ý , và , 
a)	y = 2cos+ 3	b)	y = 	c)	y = 4sin
d)	y = 	e)	y = 3 – 2sinx	f)	y = 
g)	y = 3sin – 2 	h)	y = 2 + 3cosx	i)	y = 3 – 4sin2xcos2x	
j) y = cosx + cos	k)	y = cos2x + 2cos2x 	l)	y = 
m) y = 3 – 4sinx n) y = 2 – 	 o) 	 p) 	
Trong mỡi khẳng định sau, khẳng định nào đúng? Khẳng định nào sai? Giải thích vì sao?
Trên mỡi khoảng mà hàm sớ y = sinx đờng biến thì hàm sớ y = cosx nghịch biến.
Trên mỡi khoảng mà hàm sớ y = sin2x đờng biến thì hàm sớ y = cos2x nghịch biến.
CƠNG THỨC LƯỢNG GIÁC
Hệ thức cơ bản
II. Cơng thức góc liên quan:
1. Góc đới và 2. Góc bù và 3. Góc hơn : và 4. Góc phụ nhau: và 
5.Góc hơn : và III. Cơng thức lượng giác
 1. Cơng thức cợng	2. Cơng thức nhân đơi
3. Cơng thức tích thành tổng	4. Cơng thức tổng thành tích
5. Cơng thức nhân ba	6. Cơng thức hạ bậc	
7. Cơng thức tính theo sinx , cosx , tanx theo t = 8. Các hệ thức cần nhớ:
8. Đặc biệt
§2 PHƯƠNG TRÌNH LƯỢNG GIÁC
A. Kiến thức cơ bản
1.Phương trình cơ bản – Phương trình bậc nhất theo mợt HSLG.
	Tởng quát: Nếu a là mợt giá trị khơng đặc biệt
·	sinx = a 	Û 	·	tanx = a	Û (chú ý)
·	cosx = a 	Û 	·	cotx = a	Û 
Nếu a là mợt giá trị đặc biệt: thì :
·	sinu = sinv 	Û 	·	tanu = tanv	Û (chú ý)
·	cosu = cosv 	Û 	·	cotu = cotv	Û 
Chú ý:
1. Khi gặp dấu trừ ở trước thì:
	– sinx = sin(– x)	– cosx = cos(p – x)
	– tanx = tan(– x)	– cotx = cot(– x)
Khi giải phải dùng đơn vị là rad nếu đề bài khơng cho đợ (0).
	2. Các trường hợp đặc biệt:
sinx = – 1	Û 	x = – + k2p	tanx = – 1 	Û 	x = – + kp
sinx = 0	Û 	x = kp	tanx = 0	Û 	x = kp
sinx = 1	Û 	x = + k2p	tanx = 1 	Û 	x = + kp
cosx = – 1	Û 	x = (2k + 1)p	cotx = – 1 	Û 	x = – + kp
cosx = 0	Û 	x = + kp	cotx = 0	Û 	x = + kp
cosx = 1	Û 	x = k2p	cotx = 1 	Û 	x = + kp
Phương trình bậc hai theo mợt HSLG.
Là các phương trình mà sau khi biến đởi ta được mợt trong các dạng sau (a ¹ 0):
·	asin2u + bsinu + c = 0 (1)	·	acos2u + bcosu + c = 0 	(1)
	đặt t = sinu. điều kiện: – 1 £ t £ 1. 	đặt t = cosu. điều kiện: – 1 £ t £ 1.
	(1) Û at2 + bt + c = 0	(1) Û at2 + bt + c = 0
·	atan2u + btanu + c = 0 (1)	·	acot2u + bcotu + c = 0 	(1)
	điều kiện: cosu ¹ 0.	điều kiện: sinu ¹ 0.
	đặt t = tanu, (1) Û at2 + bt + c = 0	đặt t = cotu, (1) Û at2 + bt + c = 0
Chú ý: Nếu phương trình có chứa tanu, cotu, sin2u, cos2u, tan2u, cot2u,.. đặt t = tanu, khi đó: 
, sin2u = , cos2u = , tan2u = , cot2u = .
Phương trình bậc nhất đới với sinx và cosx (Phương trình cở điển).
asinx + bcosx = c	(1) với a, b, c Ỵ R, và a2 + b2 ¹ 0
Điều kiện để phương trình cĩ nghiệm là: a2 + b2 ³ c2
Chia 2 vế phương trình cho, ta được: 
sinx + cosx = 
Vì nên đặt cosa = , sina = 
Khi đó ta được: 	sin(x + a) = rời giải như phương trình cơ bản.
Chú ý:
Ngoài ra ta có thể dùng cơng thức tính sinx, cosx theo t = . 
Sau đây là cách giải:
Đặt t = . điều kiện x ¹ p + k2p
Þ 	sinu = 	và	cosu = 
(1) Û a. + b. = c Û (a + c)t2 – 2bt + c – a = 0 (2)
Giải (2) tìm nghiệm t1, t2 nếu có, rời sau đó giải phương trình = t1, = t2 để tìm nghiệm x (phải thỏa điều kiện)
Nếu a = b có thể dùng cơng thức sau để giải:
sinx ± cosx = sin(x ± ) = cos(x )
Phương trình thuần nhất bậc hai, bậc ba đới với sinx và cosx (Phương trình đẳng cấp).
	asin2x + bsinxcosx + ccos2x = 0	(1)
	Hoặc	a¢sin2x + b¢sinxcosx + c¢cos2x = d	(2)
(2)	Û a¢sin2x + b¢sinxcosx + c¢cos2x = d(sin2x + cos2x)
	Û (a¢– d)sin2x + b¢sinxcosx + (c¢– d)cos2x = 0 	(2¢)
Phương trình (2¢) cũng là dạng (1), nên ta chỉ xét dạng (1). Nếu gặp dạng (2) thì ta đưa về dạng (1) như trên. 
Sau đây là cách giải dạng (1):
Nếu a = 0 và b, c ¹ 0 thì (1) 	Û cosx.(bsinx + ccosx) = 0 Û 
Nếu c = 0 và b, a ¹ 0 thì (1) 	Û sinx.(asinx + bcosx) = 0 Û 
Nếu a, b, c ¹ 0:
Kiểm tra xem với cosx = 0 thì (1) có thỏa hay khơng? (cosx = 0 thì sinx = ± 1). Nếu thỏa thì kết luận rằng phương trình có 1 họ nghiệm là x = + kp (k Ỵ Z).
Với cosx ¹ 0, chia 2 vế của (1) cho cos2x, ta được phương trình:
	atan2x + btanx + c = 0	(1¢)
	(1¢) là phương trình bậc 2 theo tanx, ta đã biết cách giải (Xem phần 2).
Nghiệm của (1) là nghiệm của (1¢) và x = + kp (nếu có).
Chú ý: Ngoài ra ta có thể dùng cơng thức hạ bậc để đưa (1) về dạng phương trình bậc nhất theo sinx và cosx (Phần 3). Với: , , 
Phương trình đẳng cấp bậc 3: asin3x + bsin2xcosx + c.sinxcos2x + dcos3x = 0 giải tương tự như đẳng cấp bậc 2.
Phương trình đới xứng – Phản đới xứng.
Dạng1: 	a(sinx + cosx) + bsinxcosx = c	(1)
Đặt t = sinx + cosx = sin(x + )	Điều kiện: –£ t £
Û t2 = 1 + 2sinxcosx	 Û sinxcosx = 
(1) Û at + b. = c	Û bt2 + 2at – b – 2c = 0	(2)
Giải phương trình (2), chọn nghiệm thỏa điều kiện: –£ t £
Giải phương trình sin(x + ) = t để tìm x.
Dạng 2: ( phản đới xứng )	a(sinx – cosx) + bsinxcosx = c	(1)
Đặt t = sinx – cosx = sin(x – )	Điều kiện: –£ t £
Û t2 = 1 – 2sinxcosx	 Û sinxcosx = 
(1) Û at + b. = c	Û bt2 – 2at – b + 2c = 0	(2)
Giải phương trình (2), chọn nghiệm thỏa điều kiện: –£ t £
Giải phương trình sin(x – ) = t để tìm x.
Dạng 3: 	a|sinx ± cosx| + bsinxcosx = c 	(1)
Đặt t = |sinx ± cosx| = 	Điều kiện: 0 £ t £. Giải tương tự như trên. 
Phương trình lượng giác khơng mẫu mực.
Trường hợp 1: Tởng hai sớ khơng âm:	 
Trường hợp 2: Phương pháp đới lập: 	
Trường hợp 3: Sử dụng tính chất :	
·	sinu + sinv = 2 	 	·	sinu – sinv = 2 	 
·	sinu + sinv = – 2 	 	·	sinu – sinv = – 2 	 
·	Tương tự cho các trường hợp cosu ± cosv = ± 2 và cosu ± cosv ± 2.
Trường hợp 4: Sử dụng tính chất :	
·	sinu.sinv = 1 	 	·	sinu.sinv = –1 
·	Tương tự cho các trường hợp cosu.cosv = ±1, sinu.cosv = ±1, cosu.sinv = ±1.
Bài tập ứng dụng:
1. Phương trình cơ bản – phương trình bậc nhất mợt HSLG
Bài 1. Giải các phương trình sau:
1)	sinx = – 	2)	sinx = 	3)	sin(x – 600) = 	
4)	sin2x = – 1	5)	cos(3x – ) = – 	6)	cos(x – 2) = 
7)	8)	cos(2x + 500) = 	9)	tan2x = tan	
10)	tan(3x – 300) = – 	11)	12)	
13)	14)	sin4x = 	15)	
16)	cos(3x – 450) = 	17)	sin3x = – 	18)	sin(2x – 150) = 
19)	20)	cos(x + 3) = 	21)	sin2x = 	
22)	cos(2x + 500) = – 	23)	2cosx – = 0	24)	tan3x – 3 = 0
Bài 2. Giải các phương trình sau:
1)	cos2x . cot = 0	2)	
3)	(cotx + 1) . sin3x = 0	4)	sin2x . cotx = 0	
5)	tan(x – 300)cos(2x – 1500) = 0	6)	(2cos2x – 1)(2sin2x –) = 0	
8)	tan(2x + 600)cos(x + 750) = 0	7)	 (3tanx + )(2sinx – 1) = 0	
9)	(2 + cosx)(3cos2x – 1) = 0	10) 	(sin2x – 1)(cosx + 1) = 0
Bài 3. Giải các phương trình sau:
1)	sin(2x – 150) = với – 1200 < x < 900	2)	cos(2x + 10 = 	với – p < x < p 
3)	sin	với 0 < x < 2p	4)	tan	với 0 < x < p
5)	sinx = – 	với – p < x < 0	6)	cos(x – 2) = 	với x Ỵ [0 ; p]
7)	tan(x – 100) = 1 	với – 150 < x < 150	8)	sin= 1 	với x Ỵ [p ; 2p]
Bài 4. Giải các phương trình sau:
1)	cos3x – sin2x = 0	2)	tanx tan2x = – 1
3)	sin3x + sin5x = 0	4)	cot2x cot3x = 1
5)	sinx – cos(x + 600) = 0 	6)	6) cos(x – 100) + sinx = 0
7)	8)	
9)	sin3x = cos2x	10)	cosx = – sin2x
11)	sin2x + cos3x = 0	12)	tan(3x + 2) + cot2x = 0
13)	tanx . tan3x = 1	14)	cot2x.cot(x + 450) = 1
15)	 = 0	16)	 = 0
17)	tan3x + tanx = 0	18)	tan3x + tan(2x – 450) = 0
Bài 5. Giải các phương trình sau:
1)	sin2x = 	2)	4cos2x – 3 = 0 	3)	sin23x – cos2x = 0	
2. Phương trình bậc hai – bậc ba mợt HSLG
Bài 6. Giải các phương trình sau:
1)	2cos2x – 2( + 1)cosx + + 2 = 0	2)	2cos2x + 4sinx + 1 = 0	
3)	cos2x + 9cosx + 5 = 0	4)	sin2x – 2cos2x + = 0	
5)	cos5x.cosx = cos4x.cos2x + 3cos2x + 1	6)	cot4x – 4cot2x + 3 = 0
7)	cos2(x + ) + 4cos() = 	8)	tan2x – + 5 = 0
9)	 – 1 + tanx – (tanx + 1) = 0	10)	cos4x – 3 + 2 = 0 
11)	2cos2x + cosx – 2 = 0	12) 	2cos2x – 3cosx + 1 = 0
13)	6sin2x – 5sinx – 4 = 0	14)	
15)	16)	
17)	18)	cos2x + sinx + 1 = 0	
3. Phương trình bậc nhất đới với sinx và cosx (Phương trình cở điển).
Bài 8. Giải các phương trình sau:
1)	sinx – cosx = 	2)	cosx + sinx = – 3) sin4x + cos4x = 	
4)	2sinx – 9cosx = 	5)	cos(2x – 150) + sin(2x – 150) = – 1 	6) cosx + 4sinx + 1 = 0
7)sin2x + 3cos2x = 4 	8)	2sinx – 2 cosx = 	9) sin2x – cos2x = 1
10)	cosx –sinx = 	11)	3sin3x – 4cos3x = 5	12) 5cos2x + 12sin2x – 13 = 0	
13)	3sinx + cosx = 1
Bài 9. Giải các phương trình sau:
1)	2sin22x + sin4x = – 3 	2) 	cosx +sinx = 2 cos
3)	3sin3x – cos9x = 1 + 4sin33x	4)	5cos(2x + 180) – 12sin(2x + 180) = –13 
5)	2cos + 3cos= 	6) 	sin2x + sin2x = 
7)	2sin2x + sin2x = 3	8)	3cos2x – sin2x – sin2x = 0
9)	sin9x + cos7x = sin7x + cos9x	10)	sin5x + cos5x = cos13x
11)	8sin2 – 3sinx – 4 = 0 	12)	
13)	14) 	 3cosx – 4sinx + = 3
Bài 10. Tìm giá trị nhỏ nhất, lớn nhất của các hàm sớ sau:
1)	y = 2sinx + cosx + 1	2) 	y = 2sin2x + 4sinxcosx + 3
3)	y = sin2x + cos2x – 2 	4)	y = 
Phương trình thuần nhất bậc hai, bậc ba đới với sinx và cosx (Phương trình đẳng cấp).
Bài 11. Giải các phương trình sau:
1)	2sin2x + sinxcosx – 3cos2x = 0	2) 	3sin2x – 4sinxcosx + 5cos2x = 2
3)	sin2x + sin2x – 2cos2x = 	4)	2cos2x + sin2x – 4sin2x = – 4 
5)	sin2x – 10sinxcosx + 21cos2x = 0	6)	cos2x – 3sinxcosx + 1 = 0
7)	cos2x – sin2x – sin2x = 1	8) 	2cos2x – 3sinxcosx + sin2x = 0
9)	3sin2x – 2sinxcosx + cos2x – 1 = 0	10)	4sin2x – 3sin2x – 2cos2x = 4
11)	3cos2x + sinxcosx + 2sin2x = 2	12)	3cos2x + 3sinxcosx + 2sin2x = 1
13	cos2x – sin2x – sin2x = 1	14) 	sin2x + 2cos2x – 1 = 0
15)	2cos2x + 3sin2x – 8sin2x = 0	16)	3cos2x + 2sin2x – sin2x = 2 + 
17)	sin3x + cos3x = sinx + cosx	18)	sin3x + 2sin2xcosx – 3cos3x = 0
19)	sin3x – 5sin2xcosx – 3sinxcos2x + 3cos3x = 0	20) 	cos3x – 4cos2xsinx + cosxsin2x + 2sin3x = 0
Phương trình đới xứng – Phản đới xứng.
Bài 12. Giải các phương trình sau:
1)	5sin2x – 12(sinx – cosx) + 12 = 0	2) 	(cosx – sinx) + 2sin2x – 1 = 0 
3)	2½sinx + cosx½+ 3sin2x = 2	4)	½sinx – cosx½+ 4sin2x = 1
5)	tanx + cotx = (sinx + cosx)	6)	(1 + sin2x)(cosx – sinx) = cos2x
7)	3(sinx + cosx) – sin2x – 3 = 0	8) 	2sin4x + 3(sin2x + cos2x) + 3 = 0
9)	cosx + + sinx + = 	10)	sin2x – sin + 1 = 0
Phương trình lượng giác khơng mẫu mực.
Bài 13. Giải các phương trình sau:
1)	sin25x + 1 = cos23x	2) 	sin2x – 2sinx + 2 = sin23x
3)	sinx + cosx = (2 – sin3x)	4)	2cos2x = 3sin25x + 2
5)	(cos4x – cos2x)2 = 4 + cos23x	6)	sinx + cosx = tanx + cotx
7)	cos5x.sin3x = 1	8) 	sin2x + sin3x + sin4x = 3
 7. Phương trình dạng khác ( tởng quát )
Bài 14. Giải các phương trình sau:
1)	sin24x + sin23x = sin22x + sin2x	2) 	sin24x + sin23x + sin22x + sin2x = 2
3)	cos2x + cos22x + cos23x + cos24x = 2	4)	sin2x + sin2x = cos23x + cos24x
5)	4sin3x + sin5x – 2sinxcos2x = 0	6)	sin2x + sin22x = sin23x
7)	cos2x – cos8x + cos6x = 1	8) 	sinx + sin2x + sin3x + sin4x = 0
9)	sin2x + cos2x + sin3x = cos3x	10)	sin6x.sin2x = sin5x.sinx
11)	cos8x.cos5x = cos7x.cos4x	12)	sin7x.cosx = sin5x.cos3x
13	2tan2x – 3tanx + 2cot2x + 3cosx – 3 = 0	14) 	sin3x + sin5x + sin7x = 0
15)	cos2x + 4sin4x = 8cos6x	16)	sinx = sin5x – cosx 
17)	3 + 2sinx.sin3x = 3cos2x	18)	sinx+sin2x+sin3x = cosx+cos2x+cos3x
19)	sinx+sin2x+sin3x = 1+cosx+cos2x+cos3x	20) 	1 + cosx + cos2x + cos3x = 0
21)	tanx + cot2x = 2cot4x	22)	 2cos2x + sin10x = 1
23)	tanx + tan2x = sin3x.cosx	24)	5tanx – 2cotx = 3
25)	26)	
27)	(1 – tanx)(1 + sin2x) = 1 + tanx	28)	4sin3x = sinx + cosx
29)	30) 	sin4x + cos4x = 
 9. Phương trình lượng giác trong các đề thi Đại học – Cao đẳng
2) 	sin23x – cos24x = sin25x – cos26x	
3)	cos3x – 4cos2x + 3cosx – 4 = 0 , với x Ỵ [0 ; 14] 
5) 	
6) 
Hết
CHƯƠNG II: HỐN VỊ - CHỈNH HỢP – TỔ HỢP
§1. Quy tắc đếm
1) Quy tắc cộng:
Thực hiện 1 cơng việc được thực hiện bởi k phương án.
Phương án 1 cĩ n1 thực hiện.
 “ 2 “ n2 “ .
.
Phương án k cĩ nk cách thực hiện
Thì ta cĩ n1+ n2 + ..+ nk cách thực hiện.
Phát biểu dưới dạng khái niệm tập hợp: Nếu A và B là các tập hợp hữu hạn khơng giao nhau thì:
n(AB) = n(A) + n(B)
2) Quy tắc nhân:
Một cơng việc được thực hiện bởi hai hay nhiều hành động mà trong đĩ :
 Cĩ m cách thực hiện hành động thứ nhất
	 Cĩ n cách thực hiện hành động thứ hai
	 .
	 Cĩ i cách thực hiện hành động thứ k
Thì ta cĩ : m.ni cách thực hiện.	
BÀI TẬP ÁP DỤNG
Dạng 1 : Sử dụng qui tắc cộng
Bài 1: Trên kệ sách có 12 quyển sách tham khảo Toán 11 và 6 quyển sách tham khảo Lý 11. Hỏi học sinh đó có bao nhiêu cách chọn mợt trong hai loại sách nói trên
Bài 2: Cho tập hợp E = {a,b,c}. Có bao nhiêu cách chọn mợt tập hợp con khác rỡng của E.
Bài 3: Từ các số 1, 2, 3 cĩ thể lập được bao nhiêu số tự nhiên bé hơn 100.
	Dạng 2: Sử dụng qui tắc nhân
Bài 4: 
1) Từ nhà An đến nhà Bình cĩ 5 con đường để đi, từ nhà Bình đến nhà Tồn cĩ 3 con đường để đi. Hỏi cĩ bao cách đi tù nhà An đến nhà Tồn?
Từ các sớ 1,3, 5, 6, 8.Cĩ thể lập được bao nhiêu số tự nhiên chẵn gồm 3 chữ số 
a) Các số tự nhiên cĩ chữ số giống nhau.
b) Các số tự nhiên cĩ chữ số khác nhau.
Bài 5: Trên kệ có 3 quyển toán khác nhau, 5 quyển lí khác nhau và 7 quyển hóa khác nhau. Hỏi có bao nhiêu cách chọn.
a, Mợt quyển sách?	b, Ba quyển sách khác nhau?	c, Hai quyển sách khác nhau?
Bài 6: Cu đến cửa hàng văn phòng phẩm để mua quà tặng bạn Đen, trong cửa hàng có ba mặt hàng thích hợp: đó là 5 loại bút, 4 loại vở và 3 loại thước. Hỏi bạn Cu có bao nhiêu cách chọn mợt món quà gờm bút, vở và thước để tặng bạn Đen? 
Bài 7: Trong mợt đợi văn nghệ có 8 nam và 6 bạn nữ. Hỏi có bao nhiêu cách chọn mợt đơi song ca gờm có:
a, Hai nam?	b, Hai nữ	c, Mợt nam và mợt nữ	
Bài 8: Từ các sớ 1, 2, 3, 4, 5, 6, 7. Hỏi có thể lập được bao nhiêu sớ tự nhiên trong đó:
	a, Sớ có ba chữ sớ?	b, Sớ có ba chữ sớ khác nhau?
 c, Có bao nhiêu sớ chẵn có ba chữ sớ? 	d, Có bao nhiêu sớ chẵn có ba chữ sớ khác nhau?
 e, Có bao nhiêu sớ lẻ có bớn chữ sớ?	f, Có bao nhiêu sớ lẻ có bớn chữ sớ khác nhau?
Bài 9: Một tập thể gồm 14 người gồm 6 nam và 8 nữ, người ta muốn chọn 1 tổ cơng tác gồm 6 người.Tìm số cách chọn sao cho trong tổ phải cĩ 2 nam và 4 nữ
Bài 10: Cĩ bao nhiêu số tự nhiên gồm 4 chữ số sao cho khơng cĩ chữ số nào lặp lại đúng 3 lần?
Bài 11: Từ 1 nhĩm học sinh gồm 7 nam và 6 nữ. Thầy giáo cần chọn ra 5 em tham dự lể mít tinh tại trường với yêu cầu cĩ 2 nam và 3 nữ. Hỏi cĩ bao nhiêu cách chọn.
§2. Hốn vị - chỉnh hợp – Tổ hợp
Nợi dung
Định nghĩa
Cơng thức
CT Khác
Hốn vị
Cho tập A gồm N ptử. Mỗi kq Sx n ptử là 1 HV
P(n) = n!
Pn = 1.2.3..n = n!
Chỉnh hợp
n(A)= n. Mỗi cách chọn k ptử cĩ thứ tự của A được gọi là 1 chỉnh hợp chập k của n ptử.
=
Pn =
0! = 1
Tổ hợp
n(A)= n. Mỗi tập con gồm k ptử của A được gọi là 1 tổ hợp chập k của n ptử.
=
Bài 12:
a) Hỏi cĩ bao nhiêu cách sắp xếp 10 người vào 10 cái ghế xếp thành 1 hàng ngang.
b) Mợt lớp học cĩ 35 hs trong đó 15 nam và 20 nữ. Hỏi cĩ bao nhiêu cách chọn 
1) 5 bạn để đi dự hội trại của Đồn Trường.
2) 5 bạn trong đó gờm 2 nam và 3 nữ 
3) 3 bạn trong đó gờm 1 bạn làm lớp trưởng, 1 bạn lớp phĩ và 1 bạn bí thư đồn.
Bài 13: Trên giá sách cĩ 10 quyển sách tốn, 8 quyển sách văn và 3 quyển sách lý, lấy 3 quyển.Tính số cách lấy để:
a) Mỗi loại cĩ 1 quyển.
b) Cả 3 quyển cùng loại.
c) Chỉ cĩ đúng 1 quyển sách văn.
d) Cĩ ít nhất 1 quyển tốn.
Bài 14: Một nhĩm gồm 10 học sinh, trong đĩ 7 nam và 3 nữ. Hỏi cĩ bao nhiêu cách sắp xếp 10 học sinh trên thành 1 hàng dọc sao cho 7 học sinh nam phải đứng liền nhau.
Bài 15: Từ các sớ 1, 2, 3, 4, 5, 6, 7. Hỏi có thể lập được bao nhiêu sớ tự nhiên trong đó:
	a, Sớ có ba chữ sớ?	b, Sớ có ba chữ sớ khác nhau?
 c, Có bao nhiêu sớ chẵn có ba chữ sớ? 	d, Có bao nhiêu sớ chẵn có ba chữ sớ khác nhau?
 e, Có bao nhiêu sớ lẻ có bớn chữ sớ?	f, Có bao nhiêu sớ lẻ có bớn chữ sớ khác nhau?
Bài 16: Từ các sớ 1, 2, 3, 4, 5, 6, 7, 8, 9. Hỏi có thể lập được bao nhiêu sớ tự nhiên trong đó:
a, Sớ có hai chữ sớ? 	b, Sớ có hai chữ sớ khác nhau?
c, Sớ có ba chữ sớ?	d, Sớ có ba chữ sớ khác nhau?
e, Sớ có bớn chữ sớ?	f, Sớ có bớn chữ sớ khác nhau?
g, Có bao nhiêu sớ chẵn có ba chữ sớ?	h, Có bao nhiêu sớ chẵn có ba chữ sớ khác nhau?
i, Có bao nhiêu sớ lẻ có ba chữ sớ?	j, Có bao nhiêu sớ lẻ có ba chữ sớ khác nhau?
k) Có bao nhiêu sớ có ba chữ sớ chia hết cho 5 	l) Có bao nhiêu sớ có ba chữ sớ khác nhau chia hết cho 5
Bài 17: Hỏi từ các chữ số 1,2,3,4,5,6,7,8,9 cĩ thể lập được bao nhiêu số tự nhiên gồm 5 chữ số khác nhau sao cho trong chữ số đĩ cĩ mặt chữ số 1 ở hàng đơn vị.
Bài 18: Cĩ 6 học sinh sẽ được sắp xếp vào 6 chỗ đã được ghi số thứ tự trên bàn dài. Tìm số cách sắp xếp 6 học sinh này sao cho hai học sinh A và B khơng ngồi cạnh nhau.
Bài 19: Cĩ 6 học sinh sẽ được sắp xếp vào 6 chỗ đã được ghi số thứ tự trên bàn dài. Tìm số cách sắp xếp 6 học sinh này ngồi vào bàn.
Bài 20: Trong mợt tở có 10 bạn. Hỏi có bao nhiêu cách phân cơng ba bạn trực nhật ( mỡi bạn chỉ làm mợt nhiệm vụ ) được chọn từ các bạn đó?
Bài 21: Trong hợp đựng 7 quả cầu màu đỏ và 3 quả cầu xanh ( hoàn toàn giớng nhau về hình thức ), lấy ngẫu nhiên 3 quả. Hỏi 
a, Có bao nhiêu cách như vậy?
b, Có bao nhiêu cách lấy để trong đó có hai quả màu đỏ?
c, Có bao nhiêu cách lấy để trong đó có nhiều nhất hai quả màu đỏ?
d, Có bao nhiêu cách lấy để trong đó có ít nhất mợt quả màu đỏ?
Bài 22: Giải phương trình : trong đó là sớ hoán vị của x phần tử và là sớ chỉnh hợp chập 2 của x phần tử
Bài 23: Giải phương trình : (x là sớ nguyên dương , là sớ tở hợp chập k của n phần tử)
Bài 24: Giải phương trình 
a) 	b) 
Bài 25: Giải bất phương trình : 
§3. Nhị thức Niu – Tơn:
Dạng khai triển:
 (1)
Với a=b=1, 2n = . Với a= 1, b = -1 ta cĩ 0 = 
Chú ý: a) Số các hạng tử trong (1) là n+1
	b) Số mũ của a giảm dần , số mũ của b tăng dan dần từ trái sang phải. nhung tong các số mũ bắng n
	c) Các hệ số của mỗi hạng tử cách đều 2 hạng tử đầu và cuối thì bằng nhau.
	d) Sớ hạng tởng quát 
Bài 26
1) Khai triển các biểu thức sau:
a) 	b) 	c) 	d) 	e) (2x – 3y)4	f) (y + 2x)5 	
g) 	h) 	 i) 	j) 	k) 	 l) 
2) Tìm hệ số khơng chứa x trong khai triển:	a) (2x + )6	b) (2x + )8	
Bài 27: Cho biểu thức 
a, Khai triển biểu thức trên thành tởng các đơn thức?
b, Tìm hệ sớ của trong khai triển biểu thức trên?
Bài 28: Cho biểu thức 
a, Tìm hệ sớ của trong khai triển biểu thức trên?
b, Tìm sớ hạng khơng chức trong khai triển biểu thức trên?
Bài 29: Cho biết hệ sớ của sớ hạng thứ ba trong khai triển bằng 5. Tìm sớ hạng ở giữa trong khai triển?.
Bài 30: Cho biểu thức 
a, Tìm các sớ hạng thứ 1, 2, 3 trong khai triển biểu thức trên?
b, Biết tởng của ba hệ sớ của ba sớ hạng trên bằng 11. Tìm hệ sớ của sớ hạng chứa ?
Tam giác Pascan (xem lại sgk)
§4. Phép thử và biến cố
* Phép thử ngẫu nhiên: là phép thử ta khơng đốn trước được kết quả, mặc dù đã biết tập hợp các kết quả cĩ thể xảy ra.
* Khơng gian mẫu: tập hợp các kết quả cĩ thể xảy ra của phép thử được gọi là khơng gian mẫu. K/h: 
* Biến cố: biến cố là tập con của khơng gian mẫu (KGM).
Tập được gọi là biến cố khơng, Tập được gọi là biến cố chắc chắn
Phép tốn trên các biến cố: \A được gọi là biến cố đối của biến cố A. K/h : 
a) AB được gọi là hợp của 2 biến cố.
b) AB được gọi là giao của 2 biến cố.
AB = , A và B được gọi là là 2 biến cố xung khắc
Bài tập áp dụng:
Bài 31: Gieo đờng tiền liên tiếp 3 lần. 
a) Hãy mơ tả khơng gian mẫu? 
b)Xác định các biến cố sau.
1) Mặt sấp xuất hiện ít nhất 1 lần
2) Lần đầu xuất hiện mặt ngửa
3) Mặt sấp khơng xuất hiện lần nào
4) Mặt sấp xuất hiện đúng hai lần
Bài 32 : Gieo con súc sắc 2 lần. 
a) Hãy mơ tả khơng gian mẫu. 
b) Xác định các biến cố 
1) Tổng số chấm trong 2 lần gieo là 8
2) Lần đầu xuất hiện mặt 5 chấm
3) Cả 2 lần gieo là như nhau
4) Tởng sớ chấm trong hai lần gieo nhỏ hơn 5
5) Tích sớ chấm trong hai lần gieo là sớ chẵn
Bài 33: Mợt hợp chứa 3 bi đỏ và 2 bi xanh. Lấy ngẫu nhiên từ hợp đó ra hai bi
a) Mơ tả khơng gian mẫu
b) Xác định các biến cớ
	1) Lấy được hai bi đỏ
	2) Lấy được hai bi xanh
	3) Lấy được hai bi cùng màu
Bài 34: Mợt hợp chứa 5 bi đỏ và 7 bi xanh. Lấy ngẫu nhiên từ hợp đó ra ba bi
a) Mơ tả khơng gian mẫu
b) Xác định các biến cớ
	1) Lấy được ba bi đỏ
	2) Lấy được ba bi xanh
	3) Lấy được mợt đỏ và hai xanh
	4) Lấy được ít nhất hai bi màu xanh
	5) Lấy được ít nhất mợt bi đỏ
6) Lấy được đúng hai bi đỏ
	7) Lấy được hai bi cùng màu
§5. Xác suất của biến cố
P(A) = 
P(A): xác suất của biến cố A. : là số phần tử của kgm.n(A): số phần tử của biến cố A.
Tính chất của xác suất:
.
0P(A) 1, với biến cố A.
Nếu A và B xung khắc thì 
P(AB) = P(A) + P(B)
Hệ quả: P () = 1 - P(A) 
Biến cố độc lập cơng thức nhân xác suất:
Nếu sự xảy ra của 1 biến cố khơng ảnh hưởng đến xác suất của 1 biến cố khác thì ta nĩi 2 biến cố đĩ độc lập.
A và B là 2 biến cố độc lập khi và chỉ khi:
P(A.B) = P(A).P(B)
Mợt vài ví dụ minh họa về xác suất của biến cớ
VD1 : Gieo mợt đờng xu thì khơng gian mẫu là Ω = {N, S} . Xác suất để mặt N là 
VD2 : Gieo mợtt con súc sắc thì khơng gian mẫu là Ω = {1, 2,3, 4,5,6}. Biến cớ A = {2, 4, 6} (sớ chấm trên mặt xuất hiện là sớ chẵn).
Xác suất để mặt xuất hiện là sớ chẵn bằng : P(A) = 
VD3 : Chọn ngẫu nhiên 2 lá bài trong cỡ bài 52 lá thì sớ phần tử của khơng gian mẫu Ω là ( sớ tở hợp 52 chập 2). Biến cớ đượcc đúng mợt là xì (ách) (cơ, rơ, chuần, bích) là 2.51
Vậy xác suất của biến cớ A là P(A) = 
VD4: Gieo hai đờng xu cùng mợt lúc. Tính xác suất để được nhiều nhất mợt mặt sấp (S).
Giải
Khơng gian mẫu Ω = {SS, SN, NN, NS} gờm có 4 phần tử
Biến cớ được nhiều nhất mợt mặt S là A = {SN, NN, NS}
Vậy xác suất P(A ) = 
Bài tập áp dụng
Bài 34: Gieo ngẫu nhiên con súc sắc 2 lần. Mơ tả khơng gian mẫu. tính xác suất:
a) Mặt 6 chấm xuất hiện đúng 1 lần.
b) Tổng số chấm xuất hiện trong hai lần gieo là 7
c) Mặt 5 chấm xuất hiện ít nhất 1 lần.
Bài 35: Từ một hộp chứa 8 quả cầu đen và 6 quả cầu trắng, lấy ngẫu nhiên 4 quả. Tính xác suất sao cho
a) Bốn quả lấy ra cùng màu.
b) Cĩ ít nhất một quả màu trắng.
c) Cĩ 2 quả màu trắng và 2 quả màu đen.
Bài tập tởng hợp
Bài 36: Từ TP.Hờ Chí Minh đi đến TP.Nha Trang có thể đi bằng ơ tơ, tàu hỏa, hay tàu thủy. Mỡi ngày có 6 chuyến ơ tơ, có 4 chuyến tàu hỏa và 3 chuyến tàu thủy. Hỏi có bao nhiêu sớ lựa chọn để đi từ TP.Hờ Chí Minh đến Nha Trang?
Bài 37: Mợt lớp học có 20 học sinh nam và 15 học sinh nữ.
a) Giáo viên chủ nhiệm muớn chọn mợt học sinh nam hay nữ dự trại hè của trường. Hỏi có bao nhiêu cách chọn?
b) Giáo viên chủ nhiệm muớn chọn mợt học sinh nam và mợt học sinh nữ dự lễ hợi của trường bạn. Có bao nhiêu cách chọn?
Bài 38: Cho tập hợp E = {2, 4, 6}. Hỏi có thể lập được bao nhiêu sớ tự nhiên khác nhau nhau chọn từ các phần tử của E.
Bài 39: Trong cuợc thi vấn đáp về mơn sử. Giám khảo soạn 10 câu hỏi về sử Việt Nam, 6 câu hỏi về sử thế giới. Mỡi thí sinh rút thăm mợt câu hỏi. Hỏi mỡi thí sinh có bao nhiêu khả năng chọn mợt câu hỏi?
Bài 40: Có tất cả bao nhiêu sớ lẻ nhỏ hơn 80?
Bài 41: Giả sử có 2 đường nới từ tỉnh A đến tỉnh B và có 3 đường nới từ tỉnh B đến tỉnh C. Chúng ta muớn đi từ tỉnh A sang tỉnh C qua ngã tỉnh B và trở về theo ngã đó. Có tất cả mấy hành trình đi và nếu :
a) Phải dùng cùng mợt đường để đi và về
b) Dùng đường nào cũng được để đi và về
c) Phải dùng những đường khác nhau làm đường đi và đường về trên cả hai chặng A – B và B – C ?
Bài 42: Có tất cả mấy sớ có thể thành lập được với các chữ sớ : 2.4.6.8 nếu :
a) Sớ đó lớn hơn 200 và nhỏ hơn 600
b) Sớ đó có 3 chữ sớ khác nhau
Bài 43: Biến sớ xe máy, nếu khơng kể mã sớ vùng, gờm có 6 kí tự. Trong đó kí tự ở vị trí thứ nhất là mợt chữ cái (trong bảng 24 chữ cái), ở vị trí thứ hai là mợt chữ sớ thuợc tập hợp {1; 2; 3; 4; 5; 6; 7; 8; 9}, ở bớn vị trí kế tiếp là bớn chữ sớ chọn trong tập hợp {0; 1; 2; 3; 4; 5; 6; 7; 8; 9}. Hỏi nếu khơng kể mã sớ vùng thì có thể làm được bao nhiêu biển sớ xe máy khác nhau?
Bài 44: Có bao nhiêu sớ tự nhiên :
a) Có 4 chữ sớ mà cả 4 chữ sớ là sớ lẻ ?
b) Có 5 chữ sớ mà các chữ sớ cách đều chữ sớ đứng giữa thì giớng nhau?
Bài 45: Người ta ghi nhãn các chiếc ghế ngời trong mợt rạp hát bằng hai kí tự: kí tự ở vị trí đầu tiên là mợt chữ cái ( trong bảng 24 chữ cái) và kí tự ở vị trí thứ hai là mợt sớ nguyên dương 1; 2; . . . ; 30. Hỏi có tất cả bao nhiêu chiếc ghế được ghi nhãn khác nhau trong rạp hát?
Bài 46: Cho tập hợp sớ E = {0, 1, 2, 3, 4, 5}. Hỏi có thể thành lập bao nhiêu sớ có 3 chữ sớ khác nhau và khơng chia hết cho 3?
Bài 47: Giáo viên chủ nhiệm muớn chia 10 học sinh thành 3 nhóm, mợt nhóm gờm 5 học sinh làm cơng tác xã hợi, mợt nhóm gờm 3 học sinh làm vệ sinh và mợt nhóm gờm 2 học sinh giữ trật tự. Hỏi có mấy cách chia?
Bài 48: Trong mợt buởi tiệc mỡi ơng bắt tay với các người khác trừ vợ mình, các bà khơng người nào bắt tay nhau. Biết có tất cả 15 cặp vợ chờng tham dự tiệc, hỏi có tất cả bao nhiêu cái bắt tay của 30 người này?
Bài 49: mợt hợp đựng 6 viên bi đỏ và 4 viên bi xanh hoàn toàn giớng nhau về hình thức. Lấy ngẫu nhiên 3 viên bi. Tính xác suất của các biến cớ sau:
	a) A: “Lấy được 1 viên bi đỏ” 
	b) B: “Lấy được ít nhất 1 viên bi đỏ”
	c) C: “Lấy được ít nhất mỡi màu mợt viên bi”
	d) D: “Lấy được các viên bi cùng màu”
Bài 50: Trong mợt nhóm gờm 20 hs, trong đó 10 hs thích mơn toán, 12 hs thích mơn lí và 7 hs thích cả hai mơn toán và lí. Chọn ngẫu nhiên mợt hs làm bài tập trên bảng. Tính xác suất các biến cớ sau:
	a) A: “Học sinh đó thích ít nhất mợt trong hai mơn toán hoặc lí”
	b) B: “Học sinh đó khơng thích mơn nào trong hai mơn đó”
Bài 51: Chứng minh rằng: 
Bài 52: Chứng minh rằng: 
Bài 53: Gieo 3 đờng tiền cân đới. Gọi A là biến cớ có ít nhất mợt đờng tiền xuất hiện mặt ngửa và B là biến cớ có đúng 2 đờng tiền xuất hiện mặt ngửa.
a) Tính xác suất để có ít nhất mợt đờng tiền xuất hiện mặt ngửa
b) Tính P( A∩B ) và P(B/A).
Bài 54: Mợt hợp đựng 3 bi đỏ, 4 bi trắng và 5 bi xanh. Lấy ngẫu nhiên 3 bi. Tính xác
suất của các biến cớ sau :
A: “Lấy được ít nhất 1 bi đỏ”
B : “Lấy được 2 bi trắng”
C : “Lấy được đúng 1 bi xanh”
Bài 55: Mợt lớp học gờm 40 học sinh trong đó có: 15 học sinh giỏi toán, 10 học sinh giỏi Lí và 5 học sinh giỏi cả Toán và Lí. Chọn ngẫu nhiên mợt học sinh. Hãy tính xác suất để học sinh đó giỏi toán hay giỏi lí.
CHƯƠNG III : DÃY SỐ - CẤP SỐ
§1-PHƯƠNG PHÁP QUI NẠP TỐN HỌC
I: Phương pháp chứng minh qui nạp gồm cĩ 3 bước :
Bước 1 : Kiểm tra mệnh đề đúng với n= 1
Bước 2 : Giả thiết mệnh đề đúng với n=k
Bước 3 : Ta c/m mệnh đề đúng với n = k+1
Vd1 : Cmr " nỴN* ,ta cĩ :
	1+3+5+ .+ (2n-1) = n2
Vd2: Chứng minh " nỴN* thì :
Vd3: : Cmr " nỴN* thì n3 – n chia hết cho 3
Vd4 : Cmr " nỴN* ,ta cĩ : 3n > 3n+1
II: Bài tập áp dụng
1.	Chứng minh rằng: Với mọi n Ỵ N*:
a)	n5 – n 5	b)	62n + 3n+2 + 3n 11
c)	13n – 1 6	d)	n3 + 2n 3
e)	3n + 2n – 1 4	f)	32n – 1 8
g)	32n-1 + 2n+1 7	h) 	4.32n+2 + 32n – 36 64
i)	4n + 15n – 1 9	j) 	n3 + 11n 6
k)	16n – 15n – 1 225	l) 	n3 – n 3
m)	n3 + 3n2 + 5n 3	n)	3n3 + 15 9
o)	n7 – n 7	p)	2n3 – 3n2 + n 6
2.	Chứng minh rằng, Với mọi n Ỵ N*:
a)	1 + 2 + 3 +  + n = 	b) 
c)	d) 1 + 3 + 5 +  + (2n – 1) = n2
e)	f) 
g)	h) 3 + 9 + 27 +  + 3n = 
i)	j) 2 + 5 + 8 +  + 3n– 1 = 
k)	l) 1 – 2 + 3 – 4 + ¼ – 2n + (2n + 1) = n + 1
m)	
n)	
o)	với n ³ 1
p)	
q)	1.2 + 2.5 + 3.8 +  + n(3n – 1)