Đề kiểm tra 1 tiết chương 3 hình học lớp 8 - Năm học 2015 - 2016 thời gian làm bài 45 phút

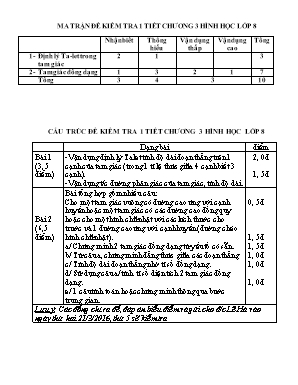
MA TRẬN ĐỀ KIỂM TRA 1 TIẾT CHƯƠNG 3 HÌNH HỌC LỚP 8
Nhận biết
Thông hiểu
Vận dụng thấp
Vận dụng cao
Tổng
Định lý Ta-let trong tam giác
2
1
3
Tam giác đồng dạng
1
3
2
1
7
Tổng
3
4
3
10
CẤU TRÚC ĐỀ KIỂM TRA 1 TIẾT CHƯƠNG 3 HÌNH HỌC LỚP 8
Dạng bài
điểm
Bài 1
(3, 5 điểm)
-Vận dụng định lý Talet tính độ dài đoạn thẳng trên 1 cạnh của tam giác (trong 1 tỉ lệ thức giữa 4 cạnh biết 3 cạnh).
-Vận dụng t/c đường phân giác của tam giác, tính độ dài.
2, 0đ
1, 5đ
Bài 2
(6,5 điểm)
Bài tổng hợp gồm nhiều câu:
Cho một tam giác vuông có đường cao ứng với cạnh huyền hoặc một tam giác có các đường cao đồng quy hoặc cho một hình chữ nhật với các kích thước cho trước và 1 đường cao ứng với cạnh huyền (đường chéo hình chữ nhật).
a/ Chứng minh 2 tam giác đồng dạng từ yếu tố có sẵn.
b/ Từ câu a, chứng minh đẳng thức giữa các đoạn thẳng 
c/ Tính độ dài đoạn thẳng nhờ tỉ số đồng dạng.
d/ Sử dụng câu a/ tính tỉ số diện tích 2 tam giác đồng dạng.
e/ 1 câu tính toán hoặc chứng minh thông qua bước trung gian.
0, 5đ
1, 5đ
1, 5đ
1, 0đ
1, 0đ
1, 0đ
Lưu ý: Các đồng chí ra đề, đáp án biểu điểm và gửi cho đ/c Lê Hà vào ngày thứ hai 21/3/2016, thứ 5 sẽ kiểm tra 
TRƯỜNG THCS VÕ THỊ SÁU
ĐỀ KIỂM TRA 1 TIẾT CHƯƠNG 3 HÌNH HỌC
LỚP 8 - Năm học 2015 -2016
Thời gian làm bài 45 phút
Bài 1 (3, 5 điểm)
a/ Cho hình vẽ.
 Tính độ dài x của đoạn MN trên hình vẽ 
b/ Cho hình vẽ.
Tính độ dài SQ và SR
Bài 2 (6, 5 điểm):
Cho tam giác ABC vuông tại A (AB < AC), đường cao AH (H thuộc BC).
a/ Chứng minh ∆ABC # ∆HAC.
b/ Chứng minh AC2 = CH. CB
c/ Biết AB = 9cm; AC = 12cm. Tính độ dài đường cao AH
d/ Gọi I và K lần lượt là hình chiếu của H trên AB và AC. Chứng minh rằng diện tích tam giác BIH bằng diện tích tam giác HKC.
------------------Hết--------------------
HƯỚNG DẪN CHẤM
Bài
Đáp án
Điểm
Bài 1 (3, 5 điểm)
a/ 2, 0 điểm
Xét nên theo định lý Talet, ta có ,
 thay số ta được 
Vậy MN = 2,6cm
1, 0
1, 0
b/ 1, 5 điểm
Xét , theo t/c đường phân giác của tam giác, ta có , thay số ta được ,
Theo t/c tỉ lệ thức, ta có 
SR = 7-= cm
Vậy SQ = cm, SR = 7-= cm
0,75
0, 5
0,25
Bài 2 (6, 5 điểm):
vẽ hình : 0,5 điểm
0, 5
a/ 1, 5 điểm
Xét hai tam giác ABC và HAC, có
0, 5
1, 0
b/ 1, 5 điểm
0, 5
1, 0
c/ 2, 0 điểm
c/ Xét tam giác ABC vuông tại A, theo định lý Pytago, ta có
BC2 = AB2 + AC2 = 92 + 122 = 81 + 144 = 225 = 152 ÞBC = 15cm
0,5
1,5
d/ 1, 0 điểm
d/ Vì IH // AC (IH và AC cùng vuông góc với AB) nên 
Xét 2 tam giác IHB và KCH có 
Þ∆IHB #∆KCH (g.g)
Vậy diện tích tam giác BIH bằng diện tích tam giác HKC.
0,25
0,75