Đề 3 thi thử tuyển sinh lớp 10 thpt năm học 2016 - 2017 môn: Toán thời gian làm bài: 120 phút

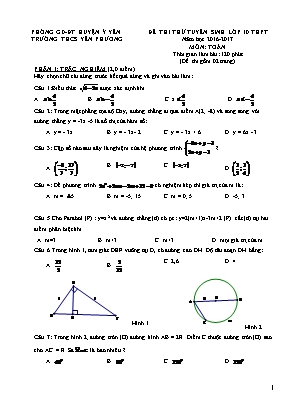
PHÒNG GD-ĐT HUYỆN Ý YÊN
TRƯỜNG THCS YÊN PHƯƠNG
ĐỀ THI THỬ TUYỂN SINH LỚP 10 THPT
Năm học 2016-2017
MÔN: TOÁN
Thời gian làm bài: 120 phút
(Đề thi gồm 02 trang)
PHẦN I: TRẮC NGHIỆM (2,0 điểm)
Hãy chọn chữ cái đứng trước kết quả đúng và ghi vào bài làm:
Câu 1:Biểu thức được xác định khi
A. B. C. x D. 
Câu 2: Trong mặt phẳng tọa độ Oxy, đường thẳng đi qua điểm A(2; -8) và song song với đường thẳng y = -3x -5 là đồ thị của hàm số:
A. y = - 3x
B. y = - 3x- 2
C. y = - 3x + 6 
D. y = 6x - 3
Câu 3: Cặp số nào sau đây là nghiệm của hệ phương trình ?
A. 
B. 
C. 
D.
Câu 4: Để phương trình có nghiệm kép thì giá trị của m là:
A. m = 5
B. m = -5; 15
C. m = 0; 5
D. -5; 3
Câu 5 Cho Parabol (P) : y=x2 và đường thẳng (d) có pt : y=2(m+1)x-3m+2.(P) cắt (d) tại hai điểm phân biệt khi
A. m=3
B. m>3 
C. m<3
D. mọi giá trị của m
Câu 6 Trong hình 1, tam giác DEF vuông tại D, có đường cao DH. Độ dài đoạn DH bằng:
A. 
B. 
C. 2,6
D. 4
 Hình 1
 Hình 2
Câu 7: Trong hình 2; đường tròn (O) đường kính AB = 2R. Điểm C thuộc đường tròn (O) sao cho AC = R. Sđ là bao nhiêu ?
A. 
B. 
C. 
D. 
Câu 8: Hình trụ có bán kính đường tròn đáy là 2cm, diện tích xung quanh là 125,6 cm2 (với ) thì chiều cao của hình trụ là: 
A. 2cm
B. 10cm
C. 6cm 
D. 4cm 
PHẦN II: TỰ LUẬN (8,0 điểm)
Câu 1 (1,25 điểm). Cho biểu thức :P=
Tìm điều kiện xác định của biểu thức P.
Rút gọn P
Câu 2(1,75 điểm) 
 Cho phương trình: x2 - 2 (m - 1)x - m - 3 = 0 (1)
 1) Giải phương trình với m = -3
2) Tìm m để phương trình (1) có 2 nghiệm thoả mãn hệ thức = 10.
3) Tìm hệ thức liên hệ giữa các nghiệm không phụ thuộc giá trị của m.
Câu 3(1,0 điểm) Cho hệ phương trình: (1)
Tìm m để hệ (1) có nghiệm (x; y) thỏa mãn: x2 + y2 = 10.
Câu 4 (3,0 điểm) 
Cho đường tròn (O;R) (điểm O cố định, giá trị R không đổi) và điểm M nằm bên ngoài (O). Kẻ hai tiếp tuyến MB, MC (B,C là các tiếp điểm ) của (O) . Vẽ đường kính BB’ của (O). Qua O kẻ đường thẳng vuông góc với BB’,đường thẳng này cắt MC và B’C lần lượt tại K và E. Chứng minh rằng:
4 điểm M,B,O,C cùng nằm trên một đường tròn.
Đoạn thẳng ME = R.
Khi điểm M di động mà OM = 2R thì điểm K di động trên một đường tròn cố định, chỉ rõ tâm và bán kính của đường tròn đó.
Câu 5 (1 điểm): Giải phương trình.
- - - - - - - - - - - - Hết - - - - - - - - - - - - - - - -
HƯỚNG DẪN CHẤM ĐỀ THI THỬ 
Phần I (Trắc nghiệm khách quan )
Câu 1
Câu 2
Câu 3
Câu 4
Câu 5
Câu 6
Câu 7
Câu 8
C
B
A
D
D
A
C
B
0.25
0.25
0.25
0.25
0.25
0.25
0.25
0.25
	 Phần II (Tự luận)
Câu
Đáp án, gợi ý
Điểm
Câu 1.1
(0,5 điểm)
Biểu thức P xác định 
0,25
0,25
Câu 1.2 (0,75 điểm)
P=
Vậy P =.
0,25
0,25
0,25
Câu 2.1 
(0,5 điểm)
*Với m = - 3 phương trình: x2 + 8x = 0 x (x + 8) = 0 
*Vậy m = -3 pt có nghiệm x=0 và x=8
0,25
0,25
Câu 2.2 
(0,75 điểm)
*Phương trình bậc hai ẩn x có 2 nghiệm 
∆’ (m - 1)2 + (m + 3) ≥ 0 m2 - 2m + 1 + m + 3 ≥ 0 
m2 - m + 4 > 0 đúng 
*Chứng tỏ phương trình có 2 nghiệm phân biệt m
Theo hệ thức Vi ét ta có: 
Ta có = 10 (x1 + x2)2 - 2x1x2 = 10 4 (m - 1)2 + 2 (m + 3) = 10
 4m2 - 6m + 10 = 10
*Vậy m = 0 ;m = 3/2 ..............
0,25
0,25
0,25
Câu 2.3
(0,5 điểm)
*Từ (2) ta có m = -x1x2 - 3 thế vào (1) ta có:
x1 + x2 = 2 (- x1x2 - 3 - 1) = - 2x1x2 - 8
 x1 + x2 + 2x1x2 + 8 = 0
*Vậy hệ thức liên hệ giữa các nghiệm không phụ thuộc m là :
x1 + x2 + 2x1x2 + 8 = 0
0,25
0,25
Câu 3
(1,0 điểm)
*Giải hệ đã cho theo m ta được:
*Với mọi giá trị của m hệ pt có nghiệm
(x;y)=(m;m+1)
*Nghiệm của hệ đã cho thỏa mãn x2 + y2 = 10
m2 + (m + 1)2 = 10 2m2 + 2m – 9 = 0. 
Giải ra ta được: .
*Vậy với m=.............
0,25
0,25
0,25
Câu 4.1
(1,0 điểm)
M
B
O
B’
C
E
K
1
2
1
1
Chứng minh M, B, O, C cùng thuộc 1 đường tròn
Ta có: MBO=900 (vì MB là tiếp tuyến)
(vì MC là tiếp tuyến)
=> MBO + MCO =
= 900 + 900 = 1800
=> Tứ giác MBOC nội tiếp
(vì có tổng 2 góc đối =1800)
=>4 điểm M, B, O, C cùng thuộc 1 đường tròn
0,25
0,25
0,25
0,25
Câu 4.2
(1,0 điểm)
Chứng minh ME = R:
Ta có MB//EO (vì cùng vuông góc với BB’) 
=> O1 = M1 (so le trong)
Mà M1 = M2 (tính chất 2 tiếp tuyến cắt nhau) => M2 = O1 (1)
C/m được MO//EB’ (vì cùng vuông góc với BC)
=> O1 = E1 (so le trong) (2)
Từ (1), (2) => M2 = E1 => MOCE nội tiếp
=> MEO = MCO = 900 
=> MEO = MBO = BOE = 900 => MBOE là hình chữ nhật
=> ME = OB = R (điều phải chứng minh)
0,25
0,25
0,25
0,25
Câu 4.3
(1,0 điểm)
Chứng minh khi OM=2R thì K di động trên 1 đường tròn cố định:
Chứng minh được Tam giác MBC đều => BMC = 600
=> BOC = 1200 
=> KOC = 600 - O1 = 600 - M1 = 600 – 300 = 300
Trong tam giác KOC vuông tại C, ta có: 
Mà O cố định, R không đổi => K di động trên đường tròn tâm O, bán kính = (điều phải chứng minh)
0,25
0,25
0,25
0,25
Câu 5
(1,0 điểm)
Ta có: x2 - 3x + 2 = (x - 1) (x - 2), x2 + 2x - 3 = (x - 1) (x + 3)
Điều kiện: x ≥ 2 (*)
Phương trình đã cho
 (thoả mãn đk (*))
Vậy phương trình đã cho có nghiệm duy nhất là x = 2.
0,25 
0,25 
0.25
0,25 
Chú ý .Học sinh làm các cách khác ,đúng vẫn cho điểm tương đương