Ôn tập môn Toán lớp 11 - Chủ đề 1: Chứng minh đường thẳng vuông góc với mặt phẳng

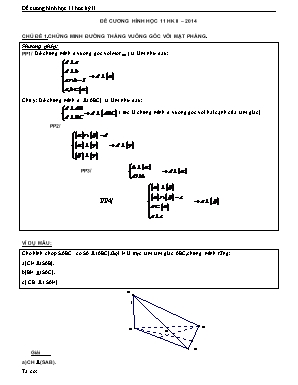
ĐỀ CƯƠNG HÌNH HỌC 11 HK II – 2014
CHỦ ĐỀ 1.CHỨNG MINH ĐƯỜNG THẲNG VUÔNG GÓC VỚI MẶT PHẲNG.
Phương pháp:
PP1/ Để chứng minh d vuông góc với mp() ta làm như sau:
Chú ý: Để chứng minh d ( ABC) ta làm như sau:
 ( tức là chứng minh d vuông góc với hai cạnh của tam giác)
 PP2/
 PP3/ 
 PP4/ 
VÍ DỤ MẪU: 
Cho hình chóp S.ABC có SA(ABC).Gọi H là trực tâm tam giác ABC,chứng minh rằng:
a)CH(SAB).
b)BH(SAC).
c) CB ( SAH)
 Giải 
a)CH(SAB).
Ta có:
 CH AB ( vì H là trực tâm tam giác ABC)
 CH SA ( vì SA(ABC) và (ABC) CH )
 CH(SAB).
b)BH(SAC).
Ta có:
 BH AC ( vì H là trực tâm tam giác ABC)
 BH SA ( vì SA(ABC) và (ABC) CH )
 BH(SAC).
c) CB ( SAH)
Ta có:
 CB AH ( vì H là trực tâm tam giác ABC)
 CB SA ( vì SA(ABC) và (ABC) CB )
 CB(SAH).
BÀI TẬP LUYỆN TẬP
Bài 1: Cho tứ diện SABC có tam giác ABC vuông tại B, SA vuông góc với (ABC).
Chứng minh BC (SAB);
Gọi AH là đường cao của tam giác SAB, AK là đường cao của tam giác SAC. Chứng minh SC (AHK). 
Bài 2:Cho tứ diện SABC có SA (ABC) . Gọi H, K lần lượt là trực tâm của các tam giác ABC, SBC. Chứng minh rằng:
AH, SK, BC đồng qui;
SC (BHK);
HK (SBC).
Bài 3:Cho hình chóp S.ABCD có đáy ABCD là hình vuông, SA (ABCD)
Chứng minh rằng BD ( SAC);
Gọi I, J lần lượt là trung điểm của SC, SD. Chứng minh IJ ( SAD ).
CHỦ ĐỀ 2: CHỨNG MINH HAI MẶT PHẲNG VUÔNG GÓC
Phương pháp: 
 Phương pháp 1: 
 Phương pháp 2: 
VÍ DỤ MẪU:
 Cho hình chóp S.ABCD đáy ABCD là hình vuông, SA ^ (ABCD).
 a) CM: (SAD) ^ (SCD)
 b) Gọi BE, DF là hai đường cao của DSBD. CMR: 
 (ACF) ^ (SBC); (ACE) ^ (SDC); (AEF) ^ (SAC)
Giải:
a) Chứng minh: (SAD) ^ (SCD)
Ta có: CD ^ DA ( vì ABCD là hình vuông)
 CD ^ SA ( vì SA ^ (ABCD) )
 CD ^ ( SAD)
 Mà CD ( SCD)
Vậy (SAD) ^ (SCD) ( đpcm)
b) * Chứng minh: (ACF) ^ (SBC) 
Ta có: DA ^ AB ( vì ABCD là hình vuông)
 DA ^ SA ( vì SA ^ (ABCD) )
 DA ^ (SAB) 
 DA ^ SB (1)
 DF ^ SB ( DF là đường cao của tam giác SBD) ( 2) 
Từ (1) và (2) SB ^ (DAF) 
 SB ^ AF (*)
Mặt khác CB ^ BA
 CB ^ SA (vì SA ^ (ABCD) )
 CB ^ (SAB)
 Mà AF (SAB)
 CB ^ AF (**)
Từ (*) và (**) AF ^ (SBC) 
 Mà AF (ACF)
Vậy (ACF) ^ (SBC) ( đpcm)
* Chứng minh (ACE) ^ (SDC)
 Chứng minh tương tự như trên
BÀI TẬP LUYỆN TẬP
Bài 1. Cho tứ diện ABCD có AB ^ (BCD). Trong DBCD vẽ các đường cao BE và DF cắt nhau tại O. trong mặt phẳng (ADC) vẽ DK ^ AC tại K. Chứng minh: (ADC) ^ (ABE); (ADC) ^ (DFK)
Bài 2. Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O. (SAD) và (SAB) cùng vuông góc với (ABCD). 
 a) CMR: SA ^ (ABCD).
 b) CM: (SBD) ^ (SAO)
Bài 3. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA ^ (ABCD). Gọi M, N là hai điểm lần lượt ở trên cạnh BC, DC sao cho BM = ; DN = . CM: (SAM) ^ (SMN).
Bài 4. Cho DABC vuông tại A. Vẽ BB' và CC' cùng vuông góc với (ABC). B’ và C’ nằm cùng phía với (ABC)
 a) CM: (ABB') ^ (ACC')
 b) Gọi AH, AK là đường cao của DABC và DAB'C'. CMR:
 (BCC'B') ^ (AHK) (AB'C') ^ (AHK)
Bài 5. Cho hình chóp S.ABCD đáy ABCD là hình vuông cạnh a, mặt bên (SAB) là tam giác đều và vuông góc với đáy. Gọi I là trung điểm của AB. CMR:
 a) SI ^ (ABCD) 	b) AD ^ (SAB)
Bài 6. Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O; AB = a; SO ^ (ABCD) và SO = ; Gọi I, J là trung điểm của AD và BC. CMR: 
 a) (SAC) ^ (SBD)	b) (SIJ) ^ (SBC)	*c) (SAD) ^ (SBC)
CHỦ ĐỀ 3:CHỨNG MINH HAI ĐƯỜNG THẲNG VUÔNG GÓC VỚI NHAU.
Phương pháp:
Để chứng minh đường thẳng vuông góc với đường thẳng ta thường dùng các cách sau:
 4/ Dùng định lý pytago đảo
Bài 1:Cho hình chóp S.ABCD có đáy là hình thang ABCD vuông ở A và B,AD=2AB=2BC.
 a)Chứng minh các mặt bên của hình chóp là những tam giác vuông.
 b)Gọi I là trung điểm của AD chứng minh BISC và CISD.
Bài 2:Cho hình chóp S.ABC có SA(ABC),AB=AC,I là trung điểm của BC AHSI.Chứng minh:
 a)BCAH.
 b)AHSB.
 *c)SC không vuông góc với AI.
*Bài 3:Cho hình chóp S.ABCD có đáy là hình vuông ,SA vuông góc với đáy .Một mặt phẳng qua A và vuông góc với SC tại N,cắt SB tại M,cắt SD tại P.
 a)Chứng minh :AMSB;ANSC;APSD.
 b)Chứng minh MPSC;MCAN
 c)Tìm diện tích thiết diện AMNP khi SA=AB=a.
Bài 4: Cho hình lăng trụ tam giác ABC.A’B’C’ có đáy ABC là tam giác đều cạnh a, cạnh bên CC’ vuông góc với đáy và CC’ = a.
Gọi I là trung điểm của BC. Chứng minh AI BC’
Gọi M là trung điểm của BB’. Chứng minh BC’ AM
Gọi K là điểm trên đoạn trên đoạn A’B’ sao cho B’K = và J là trung điểm của B’C’. Chứng minh rằng AM MK và AM KJ .
CHỦ ĐỀ 4.	XÁC ĐỊNH VÀ TÍNH GÓC GIỮA ĐƯỜNG THẲNG VÀ MẶT PHẲNG.
Phương pháp: Để xác định góc giữa đường thẳng d và mp() , ta tìm hình chiếu vuông góc d’ của d lên mp(). Khi đó góc ( d; d’) = ( d; ())
Lưu ý: Một bài toán tính góc giữa đường thẳng và mặt phẳng phải thực hiện theo 2 bước
+ Bước 1: Xác định góc giữa đường thẳng và mặt phẳng
- Tìm hình chiếu d’ của d lên ()
- 
+ Bước 2: Tính góc 
- Thường dùng tỉ số lượng giác trong tam giác vuông.
Đặc biệt chú ý bước khó khăn nhất để giải quyết bài toán là tìm hình chiếu d’ của d lên ()
VÍ DỤ MẪU:
 Cho hình chóp S.ABCD có ABCD là hình vuông cạnh a , SA vuông góc với (ABCD) và SA = a. Tính 
a) góc giữa SC với (ABCD) ;
b) góc giữa SC và (SAB)
Giải
	 a) Bước 1: + Ta có : tại A 
 AC là hình chiếu vuông góc của SC lên mặt phẳng (ABCD)
 Bước 2: + Tam giác SAC vuông tại A , có SA = a, AC = a 
b)* 
Bước 1: + Ta có CB AB ( ABCD là hình vuông) 
 CB SA ( vì SA (ABCD))
 CB (SAB) tại B
 SB là hình chiếu của SC lên mp(ABCD)
.
Bước 2: + Ta có tam giác SBC vuông tại B có CB = a; SB = a
BÀI TẬP LUYỆN TẬP
Bài 1:
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a,SA vuông góc với đáy ,SA=a.Tính góc giữa:
 a)Các cạnh bên và mặt đáy.
 b)Cạnh SC và mặt bên (SAD).
 c)Cạnh bên SB và mặt phẳng (SAC).
 *d) Cạnh AC và mp(SBC).
 *e) Cạnh SC và mp(SBD).
Bài 2:Cho tứ diện SABC có các cạnh bên SA=SB=SC=a và cùng tạo với đáy (ABC) các góc bằng nhau,biết AB=AC=2BC=a.Tính góc giữa:
 a) SA và mp(ABC).
 b) SA và mp(SBC).
Bài 3:Cho tam giác đều ABC cạnh a.Từ trung điểm H của AB kẻ đường thẳng d vuông góc với mặt phẳng (ABC).Trên d lấy điểm S sao cho .Tính góc giữa:
 a)SA với mp(ABC).
 b)SC với mp(ABC).
 c)SH với mp(SBC).
*Bài 4:Cho hình hộp ABCD.A/B/C/D/ có tất cả các cạnh đều bằng a,góc ABC bằng 1200;A/B=A/D=A/A.Tính góc giữa A/A và A/C/ với mặt phẳng đáy.
CHỦ ĐỀ 5:	XÁC ĐỊNH VÀ TÍNH GÓC GIỮA HAI MẶT PHẲNG 
Góc giữa hai mặt phẳng (P) và (Q) :
Xác định giao tuyến d của (P) và (Q)
Tìm trong (P) đường thẳng a (d) , trong mặt phẳng (Q) đường thẳng b (d)
Khi đó góc giữa (P) và (Q) là góc giữa hai đường thẳng a và b
VÍ DỤ MẪU
Cho hình chóp tứ giác đều S.ABCD có ABCD là hình vuông cạnh a, cạnh bên bằng . Tính góc giữa mặt bên với mặt đáy .
	Giải
Gọi O là tâm hình vuông thì SO vuông góc với (ABCD)	
Gọi M là trung điểm BC
Tam giác SBC cân tại S nên SM BC
O là trung điểm của BD nên OM // DC mà DC BC OM BC
	+ Ta có :
	(SBC) (ABCD) = BC
	(ABCD)OM BC 
	(SBC) SM BC 
 + Tam giác SOM vuông tại O có OM = a/2 , SM = = a
BÀI TẬP LUYỆN TẬP
Bài 1:Cho hình chóp S.ABC có đáy là tam giác cân ,AB=AC=a,góc BAC=300,SA=SB=SC=a.Tính góc giữa:
 a)(SAB) và mặt đáy.
 b)(SBC) và mặt đáy.
 c)(SAB) và (SAC).
Bài 2:Cho hình chóp S.ABC có đáy là tam giác cân ,AB=AC =a,góc BAC=1200.SA vuông góc với đáy ,SA=a.Tính góc:
 a)Giữa (SAB) và (SAC).
 b)Giữa (SBC) và (ABC),
 *c) Giữa (SBC) và (SAC) 
Bài 3:Cho hình chóp S.ABCD đáy là hình vuông cạnh a,các mặt bên là những tam giác đều cạnh a.Tính góc
 a)Giữa (SAB) và mặt đáy.
 b)Giữa (SCD) và (SBC).
Bài 4:Cho hình hộp đứng ABCD.A/B/C/D/ có đáy là hình vuông cạnh a,cạnh bên .Tính góc:
 a)Giữa (B/AC) và (ABCD).
 b)Giữa (BA/C/) và (B/AC).
VÍ DỤ VÀ BÀI TẬP TỔNG HỢP
Ví dụ 4.1: Cho hình chóp SABC có tam giác ABC vuông cân tại B, có AC = a  ; SA = a và .
1). Chứng minh 
2). Tính góc giữa hai mặt phẳng (SBC) và (ABC)
Giải
1). Chứng minh 
Ta có : 
 (1)
Theo giả thuyết ta có ABC vuông tại B
 (SAB) (2)
Từ (1) và (2) 
Mà BC (SBC), nên suy ra 
2). Tính góc giữa hai mặt phẳng (SBC) và (ABC)
Ta có : (SBC) (ABC) = BC
 BC AB (ABC) (1)
Mà AB là hình chiếu của SB lên (ABC) nên (2)
Từ (1) và (2) , suy ra 
Xét ABC vuông cân tại B có 
Xét SAB vuông tại A, có 
Vậy 
Ví dụ 4.2: Cho hình chóp S.ABCD có đáy ABCD là hình vuông và có SA vuông góc mặt phẳng (ABCD), Gọi O là giao điểm hai đường chéo AC và BD, cho SA = a, AB = a
1). Chứng minh và (SAC) (SBD)
2). Tính góc giữa hai mặt phẳng (SBD) và (ABCD)
Giải
1). Chứng minh 
Ta có : BC AB
Mà AB là hình chiếu của SB lên (ABCD)
Suy ra BC SB 
 (Định lý 3 đường vuông góc )
 CM: (SAC) (SBD)
Ta có : 
ABCD là hình vuông 
 (1)
Theo giả thuyết , SA (ABCD)
 (2)
Từ (1) và (2) , suy ra BD (SAC), mà BD (SBD)
Vậy (SAC) (SBD)
2). Tính góc giữa hai mặt phẳng (SBD) và (ABCD)
Ta có : (SBD) (ABCD) = BD
 BD AO (1)
 BD (2) ( do BD (SAC))
Từ (1) và (2) , suy ra 
 SAO vuông tại O, có , SA = a 
	.Vậy 
Bài 4.1: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, và SA vuông góc với mặt phẳng (ABCD).
1). Chứng minh các mặt bên của hình chóp là các tam giác vuông.
2). Tính góc giữa đường thẳng SC và mặt phẳng(ABCD), góc giữa mặt phẳng (SBC) và mặt phẳng(ABCD).
 Bài 4.2: Cho hình chóp tam giác đều S.ABC, có cạnh đáy bằng a, gọi O là trọng tâm của tam giác ABC, khoảng cách từ S đến mặt phẳng (ABC) bằng a.
	1). Chứng minh rằng BC SA.
	2). Tính góc giữa cạnh bên và mặt phẳng đáy.
Bài 4.3: Cho hình chóp tứ giác đều S.ABCD, có cạnh đáy bằng a, gọi O là giao điểm của AC và BD và I là trung điểm BC, SA = .
	1). Chứng minh rằng (SBC) (SOI)
	2). Tính góc giữa mặt bên và mặt phẳng đáy.
Bài 4.4: Cho hình chóp S.ABC, có SA vuông góc với mặt phẳng (ABC), tam giác ABC đều , SA = AB = . Gọi H là trung điểm BC, và AK là đường cao của tam giác SAH
	1). Chứng minh rằng AK (SBC)
	2). Tính góc giữa cạnh SC và mặt phẳng đáy.
Bài 4.5: Cho hình chóp S.ABCD, có đáy ABCD là hình vuông, tâm O, cạnh a, SA (ABCD) và SB = 
	1). Chứng minh rằng (SAO) (SBD)
	2). Tính góc giữa cạnh SC và mặt phẳng đáy.
BÀI TẬP RÈN LUYỆN TỔNG HỢP
Bài 1. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , SA vuông góc với đáy , SA = a.
Chứng minh rằng các mặt bên hình chóp là những tam giác vuông.
CMR (SAC) (SBD) .
Tính góc giữa SC và mp ( SAB ) .
Tính góc giữa hai mặt phẳng ( SBD ) và ( ABCD)
Bài 2: Cho hình chóp S. ABC có đáy ABC là tam giác vuông tại C và SB (ABC), biết AC = a, BC = a, SB = 3a.
Chứng minh: AC (SBC)
Gọi BH là đường cao của tam giác SBC. Chứng minh: SA BH.
Tính góc giữa đường thẳng SA và mặt phẳng (ABC)
Bài 3: Cho hình chóp S. ABCD có đáy ABCD là hình thoi cạnh a có góc BAD = 600 và SA=SB = SD = a
Chứng minh (SAC) vuông góc với (ABCD)
Chứng minh tam giác SAC vuông
Tính khoảng cách từ S đến (ABCD)
Bài 4: Cho hình chóp S. ABCD có đáy ABCD là hình vuông cạnh a, mặt bên (SAB) là tam giác
đều và vuông góc với đáy. Gọi E, F là trung điểm của AB và CD.
a) Cho biết tam giác SCD vuông cân tại S. Chứng minh: SE (SCD) và SF (SAB).
b) Gọi H là hình chiếu vuông góc của S trên EF. Chứng minh: SH AC
c)Tính góc giữa đường thẳng BD và mặt phẳng (SAD)
Bài 5. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, và SA = 2a.
a). Chứng minh ; 
b). Tính góc giữa SD và (ABCD); SB và (SAD) ; SB và (SAC); 
c). Tính d(A, (SCD)); d(B,(SAC))
Bài 6. Hình chóp S.ABC. DABC vuông tại A, góc = 600 , AB = a, hai mặt bên (SAB) và (SBC) vuông góc với đáy; SB = a. Hạ BH ^ SA (H Î SA); BK ^ SC (K Î SC).
a) CM: SB ^ (ABC)
b) CM: mp(BHK) ^ SC.
c) CM: DBHK vuông .
d) Tính cosin của góc tạo bởi SA và (BHK)
Bài 7: Cho hình chóp tứ giác đều S. ABCD, cạnh đáy bằng a, cạnh bên bằng . Gọi O là tâm của hình vuông ABCD. Và M là trung điểm của SC.
Chứng minh: (MBD) (SAC)
Tính góc giữa SA và mp(ABCD) .
Tính góc giữa hai mặt phẳng ( MBD) và (ABCD).
 d) Tính góc giữa hai mặt phẳng ( SAB) và (ABCD)
Bài 8: Cho hình lăng trụ ABC.A¢B¢C¢ có AA¢ ^ (ABC) và AA¢ = a, đáy ABC là tam giác vuông tại A có BC = 2a, AB = a.
a) Tính khoảng cách từ AA¢ đến mặt phẳng (BCC¢B¢).
b) Tính khoảng cách từ A đến (A¢BC).
c) Chứng minh rằng AB ^ (ACC¢A¢) và tính khoảng cách từ A¢ đến mặt phẳng (ABC¢).
----------------------------------------------Hết---------------------------------------------------------
Chúc các em học tập tốt.
MA TRẬN ĐỀ KIỂM TRA 1 TIẾT HÌNH HỌC 11 CHƯƠNG 3 – QUAN HỆ VUÔNG GÓC TRONG KHÔNG GIAN
Nội dung – Chủ đề
Mức độ
Tổng số
Nhận biết
Thông hiểu
Vận dụng
1. Vẽ hình đúng 
	1,0
	1,0
2. Chứng minh hai mặt phẳng vuông góc
1
	2,5
1
	2,5	
3. Chứng minh hai đường thẳng vuông góc
2
	2,5
1
	2,5
4. Chứng minh đường thẳng vuông góc mp
3
	2,5
1
	2,5
5. Tính góc giữa đường thẳng và mặt phẳng
4
	1,5
1
	1,5
Tổng số
1
	3,5
2
	5,0
1
	1,5
4
	10,0