Kiểm tra môn: Hình học 9, thời gian 45 phút

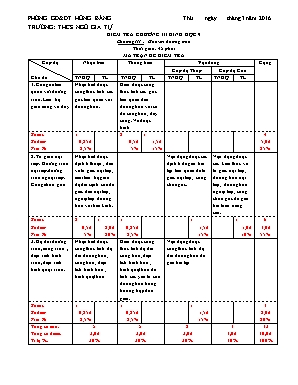
PHÒNG GD&ĐT HỒNG BÀNG Thứ ..ngày..tháng 3 năm 2016
TRƯỜNG: THCS NGÔ GIA TỰ
KIỂM TRA CHƯƠNG III HÌNH HỌC 9 
ChươngIII : Góc với đường tròn
Thời gian: 45 phút
MA TRẬN ĐỀ KIỂM TRA
Cấp độ
Chủ đề
Nhận biêt
Thông hiểu
Vận dung
Cộng
Cấp độ Thấp
Cấp độ Cao
TNKQ
TL
TNKQ
TL
TNKQ
TL
TNKQ
TL
1. Các góc liên quan với đường tròn. Liên hệ giữa cung và dây
Nhận biết được công thức tính các góc liên quan với đường tròn.
Hiểu được công thức tính các góc liên quan đến đường tròn với số đo cung tròn, dây cung. Vẽ được hình
Số câu :
Số điểm:
Tỉ lệ %:
1
0,25đ
2,5%
2
0,5đ
5%
1
1,5đ
15%
4
5,0đ
25%
2. Tứ giác nội tiếp. Đường tròn nội tiếp.đường tròn ngoại tiếp. Cung chứa góc
Nhận biết được định lí thuận , đảo về tứ giác nội tiếp, mối liên hệ giữa độ dài cạnh của đa giác đều nội tiếp, ngoại tiếp đường tròn với bán kính. 
Vận dụng được các định lí để giải bài tập liên quan đế tứ giác nội tiếp, cung chứa góc.
Vận dụng được các kiến thức về tứ giác nội tiếp, đường tròn nội tiếp, đường tròn ngoại tiếp, cung chứa góc để giải bài toán nâng cao.
Số câu :
Số điểm:
Tỉ lệ %:
2
0,5đ
5%
1
2,0đ
20%
1
0,25đ
2,5%
1
1,5đ
15%
1
1,0đ
10%
6
3,0đ
55%
3. Độ dài đường tròn, cung tròn ; diện tích hình tròn, diện tích hình quạt tròn. 
Nhận biết được công thức tính độ dài đường tròn, cung tròn, diện tích hình tròn , hình quạt tròn 
Hiểu được công thức tính độ dài cung tròn, diện tích hình tròn , hình quạt tròn để tính các yếu tố của đường tròn trong trường hợp đơn giản.
Vận dụng được công thức tính độ dài đường tròn để giải bài tập
Số câu :
Số điểm:
Tỉ lệ %:
1
0,25đ
2,5%
1
0,25đ
2,5%
1
1,5đ
15%
3
2,0đ
20%
Tổng số câu:
Tổng số điểm:
Tỉ lệ %:
5
3,0đ
30%
5
3,0đ
30%
2
3,0đ
30%
1
1,0đ
10%
13
10,0đ
100%
PHÒNG GD&ĐT HỒNG BÀNG Thứ ..ngày..tháng 3 năm 2016
TRƯỜNG: THCS NGÔ GIA TỰ
Họ và tên: 	KIỂM TRA 
 Lớp: 9A...... Môn: Hình học 9, thời gian 45 phút	
ĐỀ CHẴN
A)Phần trắc nghiệm:(2điểm). Chọn câu trả lời đúng 
Câu 1: Cho tam giác ABC nội tiếp (O), khoảng cách từ O đến cạnh AB, AC, BC lần lượt là OI, OK, OL. Cho biết OI < OL < OK. Cách sắp xếp nào sau đây đúng:
 A. << B.<< C. << D.<<
Câu 2: Cho tam giác ABC có nội tiếp đường tròn (O). Khi đó ta có :
 A. B. sđ C. D. 
Câu 3: Tứ giác ABCD nội tiếp đường tròn có . Vậy số đo là :
A. 600	B.1200	C.900	D. 1800
Câu 4: Độ dài đường tròn tâm O ; bán kính R được tính bởi công thức.
A. pR2	B. 2 pR	C. 	D. 2 p2R
Hình 3
O
 Câu 5: Cung nhỏ AB của đường tròn (O;R) có số đo là 1000. Cung lớn AB của đường tròn đó là một cung chứa góc a dựng trên đoạn thẳng AB với a là :
	A. 500	 ;	 B. 1000 	;	C. 2600	;	1300
 Câu 6. Trong hình 3, khẳng định nào sai?
	A. AD = BC	;	B. 
	C. 	;	D. 
Câu 7: Bán kính hình tròn là bao nhiêu nếu có diện tích là (cm2)
 A. 3 cm B. 4 cm C. 5 cm D. 6 cm
Câu 8: Cho (O;R) và cung AB có sđ.Độ dài cung (tính theo R) là:
 A. ;B. ;C. ;D. 
II. Tự luận (8 điểm): 
Bài 1.(6 điểm) Cho rABC có 3 góc nhọn, nội tiếp đường tròn (O; 2cm). Hai đường cao BD và CE cắt nhau tại H.
	a) Chứng minh tứ giác ADHE nội tiếp
	b) Chứng minh tứ giác BEDC nội tiếp
	c) Tính độ dài cung nhỏ AB
	d) Chứng minh đường thẳng OA vuông góc với DE.
Bài 2.(2 điểm) So sánh diện tích hình gạch sọc và hình để trắng trong hình vẽ bên.
PHÒNG GD&ĐT HỒNG BÀNG Thứ ..ngày..tháng 3 năm 2016
TRƯỜNG: THCS NGÔ GIA TỰ
Họ và tên: 	KIỂM TRA 
 Lớp: 9A..... Môn: Hình học 9, thời gian 45 phút	
ĐỀ LẺ
A)Phần trắc nghiệm:(2đ). Chọn câu trả lời đúng 
Câu 1: Khi đồng hồ chỉ 10 giờ thì kim giờ và kim phút tạo thành 1 góc ở tâm là bao nhiêu:
A: 300 B: 600 C: 900 D: 1200
Câu 2: Tứ giác ACBD nội tiếp đường tròn thì:
A: B: C: D: 
Câu 3: : Tứ giác ABCD nội tiếp được đường tròn khi:
A: ABCD là hình vuông B: ABCD là hình thang
C: ABCD là hình thang vuông D: ABCD là hình thang cân
O
Hình 1
C
A
B
300
O
Q
M
P
N
300
450
Hình 2
K
Câu 4: Trong hình 1, số đo bằng
A. 300	 ; B. 600 
C. 150	 ; D. 450
Câu 5: Trong hình 2, số đo bằng
 	A. 37030’ ;	B. 500	
 	C. 600	 ; 	D. 750
Câu 6: Độ dài cung tròn , tâm O, bán kính R :
A. 	B. 	C. 	D. 
Câu 7: Diện tích hình tròn tâm O, bán kính R là :
A. pR2	B. p2R	C. 	D. 
B ) Phần tự luận: 
Bài 1: ( 2,0 điểm)
Cho hình vẽ bên . 
Tính diện tích hình quạt tròn OAB có bán kính 5cm
Bài 2: ( 6 điểm)
Cho DABC nhọn nội tiếp đường tròn (O), hai đường cao 
BM, CN của DABC cắt nhau tại H. Chứng minh:
a) Tứ giác BCMN nội tiếp. Xác định tâm E của đường tròn ngoại tiếp tứ giác BCMN.
b) DAMN ∽DABC
c) Tia AO cắt đường tròn (O) tại K, cắt MN tại I. Chứng minh : Tứ giác BHCK là hình bình hành.
d) Chứng minh: AK ^ MN
PHÒNG GD – ĐT HỒNG BÀNG HƯỚNG DẪN CHẤM ĐỀ KIỂM TRA 1 TIẾT
 TRƯỜNG THCS NGÔ GIA TỰ Năm học : 2015 – 2016
 Môn : Hình Học 
A. Trắc nghiệm: ( 2 điểm)
Học sinh chọn đúng mỗi câu ghi 0.25điểm. 
Câu
1
2
3
4
5
6
7
8
Đ.án(chẵn)
B
C
A
B
D
A
D
A
Đ.án(lẻ)
B
A
A,D
B
D
C
A
B.TỰ LUẬN: (8 điểm)
ĐỀ CHẴN
Câu
Nội dung trình bày
Điểm
1.a
(2,0 đ)
Hình vẽ đúng
Chứng minh tứ giác ADHE nội tiếp
Xét tứ giác ADHE có :
(gt)
(gt)
 Do đó : 	 
Vậy tứ giác ADHE nội tiếp được đường tròn 	(tổng 2 góc đối diện bằng 1800)	 
 0,5đ
0,5đ
0,5đ
0,5đ
1.b
(1,5đ)
b) Chứng minh tứ giác BEDC nội tiếp
 Ta có: 	(gt)	
Hai đỉnh E, D kề nhau cùng nhìn đoạn BC dưới 1 góc vuông 
Vậy tứ giác BEDC nội tiếp 	
0,5đ
0,5đ
0,5đ
1.c
(1,5 đ)
Tính độ dài cung nhỏ AB
Ta có : ( t/c góc nội tiếp)
Vậy 
0,5đ
1 đ
1.d
(1đ)
Qua A vẽ tiếp tuyến xy với (O) xy OA (1)( t/c tiếp tuyến )
Ta có: (góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cùng chắn cung AC )
Ta lại có : ( vì cùng bù với )
Do đó : , là hai góc ở vị trí so le teong
Nên DE//xy (2)
Vậy OA vuông góc với DE
0,25đ
0,25đ
0,25đ
0,25đ
2
Gọi Sq là diện tích hình quạt, ta có:
Sq = (đvdt)
Gọi S là diện tích nữa hình tròn, ta có: 
S = (đvdt)
Suy ra: S = Sq
Vậy diện tích hình gạch sọc và hình để trắng bằng nhau và bằng Sq.
0.5đ
0.5đ
0.5đ
0.5đ
ĐỀ LẺ
Bài
Đáp án 
Điểm
Bài 1
( 2,0 điểm)
( 2,0 điểm)
Có = sđ ( Đ/n số đo cung~)
Mà = 1200 nên sđ= 1200
0,5
Ta có Squạt AOB = 
1,5
Bài 2
( 6,0 điểm)
Vẽ đúng hình cho câu a) 
0,5
a) ( 1,5 điểm)
Xét tứ giác BCMN có:
 ( Vì BM ^ AC, CN ^ AB )
Þ 2 đỉnh M và N kề nhau cùng nhìn cạnh BC dưới 1 góc vuông 
Nên tứ giác BCMN nội tiếp ( Dấu hiệu nhận biết tứ giác nội tiếp)
1,0
Tâm E của đường tròn ngoại tiếp tứ giác BCMN là trung điểm của BC
0,5
b) ( 1,5 điểm)
Có tứ giác BCMN nội tiếp đường tròn (E) ( cmt)
Þ ( T/c tứ giác nội tiếp)
Mà suy ra 
0,75
Xét DAMN và DABC có:
 : chung
Do đó DAMN ∽ DABC ( g.g)
0,75
c) ( 1,0 điểm)
Có ( Góc nội tiếp chắn nửa đường tròn (O))
Þ CK ^ AC
Có BM ^ AC ( gt) 
Þ CK // BM ( T/c từ vuông góc đến song song)
Có H Î BM nên CK // BH 
0,25
Có ( Góc nội tiếp chắn nửa đường tròn (O))
Þ BK ^ AB
Mà CN ^ AB ( gt) 
Suy ra BK //CN ( T/c từ vuông góc đến song song)
Có H Î CN Þ BK // CH
0,25
Xét tứ giác BHCK có:
 CK // BH ( cmt)
 BK // CH
Suy ra tứ giác BHCK là hình bình hành ( Dấu hiệu nhận biết hình bình hành - Tứ giác có các cạnh đối song song)
0,5
d) ( 1,5 điểm)
Xét tứ giác MCKI có :
 ( 2 góc nội tiếp cùng chắn của đường tròn (O))
mà ( cmt)
Þ , có là góc ngoài tại đỉnh M của tứ giác MCKI
Þ Tứ giác MCKI nội tiếp ( Dấu hiệu nhận biết tứ giác nội tiếp – Góc ngoài tại 1 đỉnh bằng góc trong tại đỉnh đối diện)
1,0
Þ( T/c tứ giác nội tiếp)
Mà ( cmt) Þ ( Vì M ÎAC)
ÞÞ MI ^ IK hay MN ^ AK tại I
0,5
Lưu ý : Học sinh làm bằng cách khác mà đúng thì vẫn cho điểm tối đa của câu đó