Kiểm tra học kì I môn : Toán 8 thời gian 90 phút

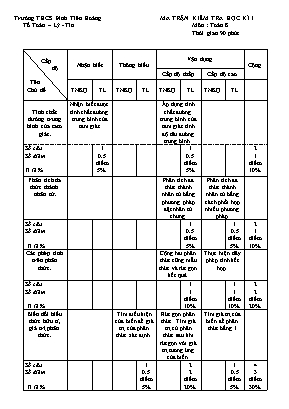
Trường THCS Đinh Tiên Hoàng MA TRẬN KIỂM TRA HỌC KÌ I
 Tổ Toán – Lý - Tin Môn : Toán 8 
 Thời gian 90 phút
 Cấp 
 độ
 Tên 
 Chủ đề 
Nhận biết
Thông hiểu
Vận dụng
Cộng
Cấp độ thấp
Cấp độ cao
TNKQ
TL
TNKQ
TL
TNKQ
TL
TNKQ
TL
Tính chất đường trung bình của tam giác.
Nhận biết được tính chất đường trung bình của tam giác
Áp dụng tính chất đường trung bình của tam giác tính độ dài đường trung bình.
Số câu 
Số điểm 
Tỉ lệ %
1
0.5 điểm 
5%
1
0.5 điểm
5%
2
1 điểm 
10%
Phân tích đa thức thành nhân tử.
.
Phân tích đa thức thành nhân tử bằng phương pháp đặt nhân tử chung.
Phân tích đa thức thành nhân tử bằng cách phối hợp nhiều phương pháp.
Số câu 
Số điểm 
 Tỉ lệ %
1
0.5 điểm 
5%
1
0.5 điểm
5%
2
1 điểm 
10%
Các phép tính trên phân thức.
Cộng hai phân thức cũng mẫu thức và rút gọn kết quả.
Thực hiện dãy phép tính kết hợp.
Số câu 
Số điểm 
 Tỉ lệ %
1
1 điểm 
10%
1
1
điểm
10%
2
2 điểm 
20%
Biến đối biểu thức hữu tỉ, giá trị phân thức.
Tìm điều kiện của biến để giá trị của phân thức xác định.
Rút gọn phân thức. Tìm giá trị củ phân thức sau khi rút gọn với giá trị tương ứng của biến.
Tìm giá trị của biến để phân thức bằng 1
Số câu 
Số điểm 
 Tỉ lệ %
1
0.5
điểm
5%
2
2
điểm
20%
1
0.5
điểm
5%
4
3
điểm
30%
Tứ giác và diện tích tứ giác
Chứng minh 1 tứ giác là hình thoi. Tính diện tích hình vuông.
Tìm điều kiện để hình thoi trở thành hình vuông
Số câu 
Số điểm 
 Tỉ lệ %
2
2
điểm
20%
1
1
điểm
10%
3
3
điểm
30%
Tổng số câu 
Tổng số điểm
Tỉ lệ %
	1
0.5 điểm 
5%
 1
0.5 điểm 
5%
7
6
điểm 
60%
4
3 điểm 
30%
12
10 điểm 
100%
=========================================
Trường THCS Đinh Tiên Hoàng KIỂM TRA HỌC KÌ I
Họ và tên :  Môn : Toán 8
Lớp : . Thời gian 90 phút
ĐIỂM
NHẬN XÉT GIÁO VIÊN
ĐỀ : 
Câu 1(1điểm) : a. Nêu tính chất đường trung bình của tam giác.
b. Cho ABC có M, N lần lượt là trung điểm của AB, AC. Cho BC = 10cm, tính độ dài MN?
 b. Cho Type equation here.Câu 2 (1 điểm) Phân tích đa thức thành nhân tử:
 a. 10x( x – y ) – 8y( x – y) b. 2xy + x2 + y2 –16
Câu 3(2 điểm) : Thực hiện các phép tính sau :
 a. b. 
Câu 4(3 điểm) : Cho phân thức 
a, Tìm điều kiện của x để giá trị phân thức A được xác định.
b, Rút gọn phân thức A
c, Tìm giá trị của phân thức A tại x = 2.
d, Tìm x để giá trị của phân thức A = 1.
Câu 5 (3 điểm). Cho hình thang cân ABCD (AB // CD ). Gọi E, N, G, M theo thứ tự là trung điểm của AB, BC, CD, DA.
 a. Chứng minh tứ giác ENGM là hình thoi.
 b. Hình thang cân ABCD cần điều kiện gì hình thoi ENGM là hình vuông.
 c. Khi ENGM là hình vuông, tính diện tích ENGM biết đường chéo AC = 16cm. 
=================== HẾT ===================
BÀI LÀM
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
ĐÁP ÁN VÀ THANG ĐIỂM
CÂU
ĐIỂM
Câu 1 : a. Đường trung bình của tam giác song song với cạnh thứ ba và có độ dài bằng 1/2 độ dài cạnh đó.
 0.5
b. A
 M N
 B C
 0.5
Câu 2 : a .
0.5
b.
0.25
0.25
Câu 3 :
a.
0.5
0.5
b. 
0.5
0.5
Câu 4 :
a.Để giá trị của A xác định thì mẫu thức 
Hay hoặc 
Hay hoặc 
0.5
b. 
1
c. Khi x = 2 thì 
1
d. Để A = 1 hay thì (vô lý)
Vậy : không có giá trị nào của x để A = 1
0.5
Câu 5 : A E B
 M N
 D G C
a. Chứng minh tứ giác ENGM là hình thoi M 
 Xét tứ giác ENGM có: 
 AE = EB ( E là trung điểm của AB)	 
 BN = NC ( N là trung điểm của BC) 
 EN là đường trung bình của ABC 
 EN // AC và EN = AC (1)
Chứng minh tương tự ta có MG là đường trung bình của ACD 
 MG // AC và MG = AC (2)
Từ (1) và (2) suy ra EN // MG và EN = MG
 Tứ giác ENGM là hình bình hành ( Tứ giác có một cặp cạnh đối vừa song song vừa bằng nhau ) 
 Chứng minh tương tự ta có ME là đường trung bình của ABD 
 ME = DB (3)
Mà AC = DB ( tính chất đường chéo hình thang cân ) (4)
Từ (1), (3) và (4) EN = ME
Vậy hình bình hành ENGM có hai cạnh kề bằng nhau nên là hình thoi. 
 0.25
 0.25
0.25
0.25
b. Để hình thoi ENGM là hình vuông thì ( hình thoi có một góc vuông là hình vuông) hay ME EN
Theo chứng minh trên: EN // AC ; ME // DB và ME EN AC DB
Vậy để tứ giác ENGM là hình vuông thì hình thang cân ABCD có hai đường chéo vuông góc với nhau.
0.25
0.5
0.25
c. Tính diện tích hình vuông ENGM, biết đường chéo AC = 16cm. 
 Ta có: EN = AC =. 16 = 8 (cm)
SENGM = EN2 = 82 = 64 ( ) 
0.5
0.5
========================================