Kiểm tra chương II môn: Hình học 7 Tuần 26 - Tiết 46

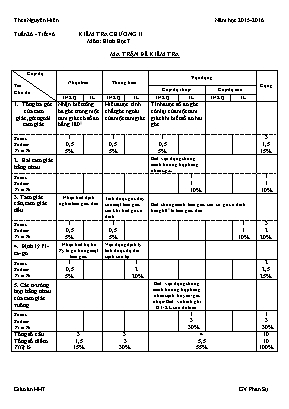
Tuần 26 - Tiết 46 KIỂM TRA CHƯƠNG II 
 Môn: Hình Học 7
 Cấp độ
Tên 
Chủ đề 
Nhận biết
Thông hiểu
Vận dụng
Cộng
Cấp độ thấp
Cấp độ cao
TNKQ
TL
TNKQ
TL
TNKQ
TL
TNKQ
TL
1. Tổng ba góc của tam giác,góc ngoài tam giác
Nhận biết tổng ba góc trong một tam giác có số đo bằng 1800
Hiểu được tính chất góc ngoài của một tam giác
Tính được số đo góc còn lại của một tam giác khi biết số đo hai góc
Số câu 
Số điểm 
 Tỉ lệ %
1 
0,5
5%
1 
0,5
5%
1 
0,5
5%
3 
1,5
15%
2. Hai tam giác bằng nhau
Biết vận dụng chứng minh trường hợp bằng nhau c.g.c.
Số câu 
Số điểm 
 Tỉ lệ %
1 
1
 10%
1 
1
 10%
3. Tam giác cân, tam giác đều
Nhận biết định nghĩa tam giác đều
Tính được góc đáy của một tam giác cân khi biết góc ở đỉnh
Biết chứng minh tam giác cân có góc ở đỉnh bằng 600 là tam giác đều
Số câu 
Số điểm 
 Tỉ lệ %
1
0,5
5%
1
0,5 
5%
1 
1
10%
3
2
20%
4. Định lý Pi-ta- go
Nhận biết bộ ba Py ta go trong một tam giác
Vận dụng định lý tính được độ dài cạnh còn lại
Số câu 
Số điểm 
 Tỉ lệ %
1
0,5
5%
1 
2
 20%
2
2,5
25%
5. Các trường hợp bằng nhau của tam giác vuông
Biết vận dụng chứng minh trường hợp bằng nhau cạnh huyền-góc nhọn- Biết vẽ hình ghi GT-KL của đề toán
Số câu 
Số điểm 
 Tỉ lệ %
1 
3
 30%
1 
3
 30%
Tổng số câu 
Tổng số điểm
Tỉ lệ %
3 
1,5
15%
3
 3
30%
4
5,5
55%
10 
10
100%
MA TRẬN ĐỀ KIỂM TRA
ĐỀ KIỂM TRA
I / TRẮC NGHIỆM : ( 3 điểm )
 Khoanh tròn chữ cái in hoa trước câu trả lời đúng.
1/ Trong ABC có + + = ?
 A . 1800 	B . 3600 	C. 1200 	D. 900
2/ Nếu là góc ngoài tại đỉnh A của ABC thì :
 A. > + B. =+ 	C. = Â + 	 	D. = Â + 
3/ Tam giác có ba cạnh bằng nhau là :
 A. Tam giác vuông B. Tam giác cân C. Tam giác tù 	D. Tam giác đều 
4/ Độ dài ba cạnh của một tam giác nào sau đây là độ dài ba cạnh của một tam giác vuông ?
 A. 3cm, 4cm, 6cm	B. 4cm, 5cm, 6cm 	C. 3cm, 4cm, 5cm 	D. 11cm, 5cm,11cm	
5/ Một tam giác cân có góc ở đỉnh bằng 1000 thì mỗi góc ở đáy sẽ có số đo là:
 A. 700	B. 400	C. 500	 	D. 800	
6/ Tam giác ABC có Â = 700; = 500 thì số đo là :
 A. 1000	B. 700	C. 800	D. 600	
II/ TỰ LUẬN : ( 7 điểm )
Cho Ot là tia phân giác của góc nhọn xOy . Lấy điểm MOt, vẽ MAOx ,
MB Oy (A Ox, BOy )
1/ Chứng minh: MA = MB . .
	2/ Cho OA = 8 cm; OM =10 cm. Tính độ dài MA.
3/ Tia OM cắt AB tại I . Chứng minh : OM là đường trung trực của đoạn thẳng AB
4/ Cho số đo góc BMA bằng 1200 , chứng minh tam giác OAB là tam giác đều.
@@@@@@@@@@@
HƯỚNG DẪN CHẤM
I/ TRẮC NGHIỆM: (3đ)
	Mỗi câu đúng cho 0,5đ
Câu
1
2
3
4
5
6
Đáp án
A
B
C
C
B
D
II/ TỰ LUẬN: (7đ)
Học sinh vẽ đúng hình đến câu a cho 0,5 đ
Ghi đúng gt và kl cho 0,5 đ
1/ Chứng minh: MA = MB ( 2 đ )
Xét hai tam giác vuông AOM và BOM có : 
OM : cạnh huyền chung
AOM = BOM ( gt)
Suy ra AOM = BOM (cạnh huyền – góc nhọn)
 Vậy MA = MB ( hai cạnh tương ứng )	
2/ Tính độ dài MA ( 2đ)
AOM vuông tại A( gt) , theo định lí Py- ta - go ta có:
OM2 = OA2 + MA2
MA2 = OM2 - OA2 = 52 – 42 = 9
Vậy 
3/ Chứng minh : OM là đường trung trực của đoạn thẳng AB ( 1 đ)
Xét AOI và BOI có : 
 OA = OB vì AOM = BOM ( cmt)
 AOM = BOM ( gt)
 OI : cạnh chung
 Do đó : AOI = BOI (c.g.c)
 => AIO = BIO , AI = BI (1)
Mà AIO + BIO = 1800 ( hai góc kề bù)
Nên AIO = BIO = = 900
 Hay (2)
Từ (1) và (2) OM là đường trung trực của đoạn thẳng AB
4/ Chứng minh tam giác OAB là tam giác đều. ( 1 đ )
 Vì AOM = BOM ( cmt)
 Nên OMA = OMB ( hai góc tương ứng )
 Mà BMA = 1200 ( gt) suy ra OMA = 600 Ta lại có AOM vuông tại A ( gt) nên hai góc nhọn OMA
 và MOA phụ nhau, suy ra MOA = 300 . Vì Ot là phân giác của góc xOy (gt) nên suy ra BOA = 600.
 Ta lại có AO = BO Vì AOM = BOM ( cmt) nên AOB cân tại O, có góc ở đỉnh BOA = 600 
 nên tam giác BOA là tam giác đều.
(học sinh làm theo cách khác đúng vẫn cho điểm tối đa)