Giáo án Một số đề thi học kì 2 tham khảo - Toán 9 – Năm học 2015 - 2016

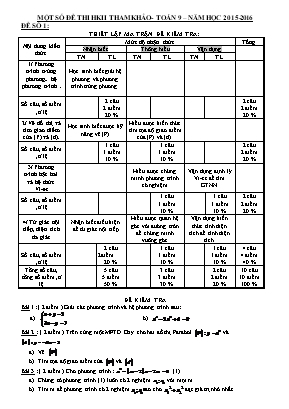
MỘT SỐ ĐỀ THI HKII THAM KHẢO- TOÁN 9 – NĂM HỌC 2015-2016
ĐỀ SỐ 1:
THIẾT LẬP MA TRẬN ĐỀ KIỂM TRA:
Nội dung kiến thức
Mức độ nhận thức
Tổng
Nhận biết
Thông hiểu
Vận dụng
TN
TL
TN
TL
TN
TL
1/ Phương trình trùng phương; hệ phương trình .
Học sinh biết giải hệ phương và phương trình trùng phương. 
Số câu, số điểm ,tỉ lệ
2 câu
2 điểm
20 %
2 câu
2 điểm
20 %
2/ Vẽ đồ thị và tìm giao điểm của (P) và (d). 
Học sinh biết được kỹ năng vẽ (P)
Hiểu được kiến thức tìm tọa độ giao điểm của (P) và (d). 
Số câu, số điểm ,tỉ lệ
1 câu
1 điểm
10 %
1 câu
1 điểm
10 %
2 câu
2 điểm
20 %
3/ Phương trình bậc hai và hệ thức Vi-et
Hiểu được chứng minh phương trình có nghiệm
Vận dụng định lý Vi-et để tìm GTNN
Số câu, số điểm ,tỉ lệ
1 câu
1 điểm
10 %
1 câu
1 điểm
10 %
2 câu
2 điểm
20 %
4/ Tứ giác nội tiếp, diện tích đa giác 
Nhận biết điều kiện để tứ giác nội tiếp 
Hiểu được quan hệ góc với đường tròn để chứng minh vuông góc
Vận dụng kiến thức tính diện tích để tính diện tích. 
Số câu, số điểm ,tỉ lệ
2 câu
2điểm
20 %
1 câu
1 điểm
10 %
1 câu
1 điểm
10 %
4 câu
4 điểm
40 %
Tổng số câu, tổng số điểm ,tỉ lệ
5 câu
5 điểm
50 %
3 câu
3 điểm
30 %
2 câu
2 điểm
20 %
10 câu
10 điểm
100 %
 ĐỀ KIỂM TRA 
Bài 1: ( 2 điểm ) Giải các phương trình và hệ phương trình sau:
 a) 	 	b) 
Bài 2 : ( 2 điểm ) Trên cùng một MFTĐ Oxy cho hai đồ thị Parabol và 
Vẽ 
Tìm tọa độ giao điểm của và .
Bài 3 : ( 2 điểm ) Cho phương trình : (1)
Chứng tỏ phương trình (1) luôn có 2 nghiệm với mọi m .
Tìm m để phương trình có 2 nghiệmsao cho đạt giá trị nhỏ nhất. 
Bài 4: ( 4 điểm ) Cho nhọn nội tiếp (O;R) . Các đường cao AD; BE; CF cắt nhau tại H.
Chứng minh : Tứ giác AEHF nội tiếp.
Chứng minh : Tứ giác BFEC nội tiếp.
Chứng minh : 
Biết số đo cung AB bằng 90 0 và số đo cung AC bằng 120 0 . 
 Tính theo R diện tích phần hình tròn giới hạn bởi dây AB; cung BC và dây AC
------- Hết -------
ĐÁP ÁN VÀ BIỂU ĐIỂM 
Bài
NỘI DUNG
ĐIỂM
1
a) Giải hpt 
1,0đ
0,5
0,5
b) Giải pt (*)
1,0đ
Đặt . PT 
0,25
( nhận ) ; ( nhận )
0,25
Với 
0,25
Vậy phương trình đã cho có 4 nghiệm :
0,25
2
a) Vẽ 
1,0đ
+ Lập bảng giá trị đúng : 
x
-2
-1
0
1
2
y = x2
4
1
0
1
4
0,5
+ Vẽ đúng đồ thị : 
0,5
b)Tìm tọa độ giao điểm của và .
1,0đ
+ Pt hoành độ giao điểm của và : 
0,25
+ 
0,25
0,25
Vậy tọa độ giao điểm của và là 
0,25
3
4
a) Chứng tỏ phương trình (1) luôn có nghiệm với mọi m .
 1,0đ
+ 
0,75
+ Vậy phương trình (1) luôn có 2 nghiệm với mọi m .
0,25
b) Tìm m để phương trình có 2 nghiệmsao cho đạt giá trị nhỏ nhất. 
1,0đ
+ Theo vi-et : 
0,25
+ 
0,25
0,25
+ Vậy GTNN của là – 12 khi 
0,25
a) Chứng minh : Tứ giác AEHF nội tiếp.
1,0đ
+ Tứ giác AEHF có: 
0,5
+ 
0,25
+ Vậy tứ giác AEHF nội tiếp đường tròn đường kính AH
0,25
b) Chứng minh : Tứ giác BFEC nội tiếp.
1,0đ
+ Tứ giác BFEC có: 
0,5
+ F và E là hai đỉnh kề nhau cùng nhìn BC dưới 1 góc 900
0,25
+ Vậy tứ giác BFEC nội tiếp đường tròn đường kính BC
0,25
c) Chứng minh : 
1,0đ
+ Kẻ tiếp tuyến x’Ax của (O) ( Cùng chắn cung AB )
0,25
+ ( BFEC nội tiếp )
0,25
+ //FE
0,25
+ Vậy : 
0,25
d) Tính theo R diện tích phần hình tròn giới hạn bởi dây AB; cung BC và dây AC
1,0đ
+ Gọi là diện tích phần hình tròn giới hạn bởi dây AB; cung BC và dây AC . 
0,25
+ (đvdt)
0,25
+ (đvdt)
0,25
+ 
(đvdt)
0,25
* Ghi chú : 
- Hình vẽ sai không chấm điểm phần bài hình
- Mọi cách giải khác đúng vẫn đạt điểm tối đa của câu đó.
ĐỀ SỐ 2:
MA TRẬN ĐỀ KIỂM TRA
Chủ đề
Nhận biết
Thông hiểu
Vận dụng
Tổng
Thấp
Cao
1. Hàm số y=ax2
- HS tính được giá trị của hàm số
Số câu
1
1
Số điểm
1
1
Tỉ lệ %
10%
10%
2. Phương trình và hệ phương trình
- HS giải được hệ PT, tìm điều kiện để PT có nghiệm duy nhất. 
- HS biết vận dụng giải phương trình trùng phương.
- HS giải được bài toán bằng cách lập PT bậc hai
Số câu
2
2
4
Số điểm
2
3
5
Tỉ lệ %
20%
30%
50%
3. Góc với đường tròn
- HS biết vẽ hình và chứng minh được tứ giác nội tiếp
- Hs vận dụng cung chứa góc để chứng minh và so sánh hai góc
Số câu
0.5
0.5
1
Số điểm
1.5
1.5
3
Tỉ lệ %
15%
15%
30%
4. Hình trụ
- HS nhớ công thức, tính được Sxq, V của hình trụ.
Số câu
1
1
Số điểm
1
1
Tỉ lệ %
10%
10%
Tổng số câu
1
3
2.5
0.5
7
Tổng số điểm
1
3
4.5
1.5
10
Tỉ lệ %
10%
30%
45%
15%
100%
ĐỀ KIỂM TRA
Bài 1: (1,0đ) Cho hàm số .Tính ; 
Bài 2: (1,0đ): Giải hệ phương trình: 
Bài 3: (1,5đ)
Giải phương trình: 
Bài 4 : (1,0đ)
Với giá trị nào của m thì phương trình: x2 -2(m +1)x + m2 = 0 có hai nghiệm phân biệt.
Bài 5: (1.5đ)
	Tích của hai số tự nhiên liên tiếp lớn hơn tổng của chúng là 19. Tìm hai số đó
Bài 6: (1,0đ) Một hình trụ có bán kính đường tròn đáy là 6cm, chiều cao 9cm. Hãy tính: 
	a) Diện tích xung quanh của hình trụ.
b) Thể tích của hình trụ.
(Kết quả làm tròn đến hai chữ số thập phân; 3,14)
Bài 7: (3,0đ) Cho tứ giác ABCD nội tiếp đường tròn đường kính AD. Hai đường chéo AC và BD cắt nhau tại E. Kẻ EF vuông góc với AD tại F. Chứng minh rằng:
	a) Chứng minh: Tứ giác DCEF nội tiếp được
 	b) Chứng minh: Tia CA là tia phân giác của .
ĐÁP ÁN VÀ BIỂU ĐIỂM:
Bài
Đáp án
Biểu điểm
1
(1,0đ)
 f(2)=2
 f(-4)=8
0,5
0,5
2
(1,0đ)
 Trừ hai PT ta được 2x=6 => x = 3, y = 1
0,75
Vậy: Hệ phương trình có nghiệm duy nhất là ( 3; 1)
0,25
3
(1,5đ)
Đặt x2 = t (ĐK t≥0)
Ta có PT : t2+3t-4 = 0
Có dạng: a + b + c = 1 +3+(-4) = 0 
0,5
 t1 = 1 ; t2 = -4 (loại)
0,25
Với t = 1 x1 = 1, x2 = -1
 0,5
Vậy: Phương trình đã cho có 2 nghiệm: x1 = 1; x2 = –1
 0,25
4
(1,0đ)
Cho phương trình: x2 – 2(m+1)x + m2 = 0 (1)
phương trình (1) luôn có 2 nghiệm phân biệt khi 
 ∆ = (m+1)2 – m2 = 2m + 1 > 0 => m > 
0,75
Vậy: Phương trình (1) có hai nghiệm phân biệt khi m > 
0,25
5
(1,5đ)
Gọi số tự nhiên thứ nhất là x (x N) =>Số thứ 2 là x+1
Tích của hai số tự nhiên liên tiếp là x(x+1)
Tổng của hai số đó là: x + x + 1 = 2x + 1
Theo bài ra ta có PT: x2 – x – 20 = 0
Có nghiệm thỏa mãn x = 5
Vậy: Hai số tự nhiên liên tiếp cần tìm là 5 và 6
0.25
0.25
0.25
0.5
0.25
6
(1,0đ)
a) Diện tích xung quanh của hình trụ là: 
Sxq = 2r.h = 2.3,14.6.9 339,12 (cm2)
0,5
b) Thể tích của hình trụ là: 
V = r2h = 3,14 . 62 . 9 1017,36 (cm3)
0,5
7
(3,0đ)
 Hình vẽ:
0,5đ
a)Ta có: = 900 ( góc nội tiếp chắn nửa đường tròn đường kính AD ) 
Xét tứ giác DCEF có: 
 = 900 ( cm trên )
 và = 900 ( vì EF ^ AD (gt) )
0,25
0,25
 => + = 1800 => Tứ giác DCEF là tứ giác nội tiếp ( đpcm )
0,5
b) Vì tứ giác DCEF là tứ giác nội tiếp ( cm phần a ) 
 => = ( góc nội tiếp cùng chắn cung EF ) (1)
 Mà: = (góc nội tiếp cùng chắn cung AB ) (2)
0,5
0,5
 Từ (1) và (2) => = hay CA là tia phân giác của ( đpcm )
0,5
( Lưu ý : Các cách làm khác đúng vẫn cho điểm tối đa) 
ĐỀ SỐ 3:
 MA TRẬN ĐỀ KIỂM TRA
 Cấp độ
Tên 
Chủ đề 
Nhận biết
Thông hiểu
Vận dụng
Cộng
Cấp độ thấp
Cấp độ cao
TL
TL
TL
TL
1. Phương trình – hệ phương trình
Số câu 
Số điểm 
 Tỉ lệ %
2
2đ 
20%
1
1đ
10%
3
3 đ 
30%
2. Đồ thị hàm số
Số câu 
Số điểm 
 Tỉ lệ %
1
1đ
10%
1
1đ
10%
2
2đ
20%
3. Phương trình bậc hai
Số câu 
Số điểm 
 Tỉ lệ %
1
1đ
10%
1
1đ
10%
2
2đ
20%
4. Đường tròn
Số câu 
Số điểm 
 Tỉ lệ %
1
1đ
10%
2
 1.5đ
15%
1
0.5đ
5%
4
3đ
30%
Tổng số câu 
Tổng số điểm
Tỉ lệ %
4
4đ
40%
3
2.5đ
25%
4
3.5đ
35%
11
10đ =100%
ĐỀ KIỂM TRA 
Câu 1 : ( 2 điểm) 
Giải phương trình, hệ phương trình sau
	a) 4x4 + 9x2 - 9 = 0
	b) 
Câu 2 : ( 2 điểm) 
Cho phương trình (ẩn x): x2 - (2m - 1)x + m2 - 2 = 0 (1)
a) Tìm m để phương trình (1) vô nghiệm.
b) Tìm m để phương trình (1) có nghiệm x1, x2 thỏa mãn 
Câu 3 : (2 điểm) 
Cho hàm số 
Vẽ đồ thị (P) của hàm số trên
Cho hàm số y = mx + 4 có đồ thị là (d). Tìm m sao cho (d) và (P) cắt nhau tại hai điểm có tung độ y1, y2 thỏa mãn 
Câu 4 : ( 3 điểm) 
Cho nửa đường tròn (O) đường kính AB. Điểm M nằm trên nửa đường tròn (M ≠ A; B). Tiếp tuyến tại M cắt tiếp tuyến tại A và B của đường tròn (O) lần lượt tại C và D.
Chứng minh rằng: tứ giác ACMO nội tiếp.
Chứng minh rằng: 
Gọi P là giao điểm CD và AB. Chứng minh: PA.PO = PC.PM
Gọi E là giao điểm của AM và BD; F là giao điểm của AC và BM. 
Chứng minh: E; F; P thẳng hàng.
Câu 5 : ( 1 điểm)
Giải phương trình 
----HẾT----
ĐÁP ÁN, BIỂU ĐIỂM: 
Câu
Đáp án
Điểm
Câu 1
(2 điểm)
a) 4x4 + 9x2 - 9 = 0 (1)
 Đặt t= x2 ()
Với 
Vậy phương trình (1) có 2 nghiệm 
0.25
0.25
0.25
0.25
b) giải hệ tìm được ( x= 2; y=1)
1
Câu 2
 (2 điểm)
a) Phương trình x2 – (2m – 1)x + m2 – 2 = 0 vô nghiệm khi 
 Û 4m2 – 4m + 1– 4m2 + 8 9/4
0,5
0,5
b) Phương trình x2 – ( 2m – 1)x + m2 – 2 = 0 có nghiệm khi 
Û 4m2 – 4m + 1– 4m2 + 8 0 Û m 9/4
0,25
 Khi đó ta có 
0,25
0,25
 Kết luận
0,25
Câu 3
(2 điểm)
a) Lập bảng và tính đúng 
 Vẽ đúng đồ thị 
0,5
0,5
b) Ta có và a.c = - 4 <0 nên phương trình có 2 nghiệm phân biệt x1, x2. Theo hệ thức Viets ta có 
Khi đó 
0,25
0,25
0,25
0,25
Câu 4
(3 điểm)
 Tứ giác ACMO nội tiếp.
Chứng minh được tứ giác ACMO nội tiếp
1
 Chứng minh rằng: 
- Chứng minh được 
- Chứng minh tứ giác BDMO nội tiếp
- Chứng minh được 
Suy ra 
0.25
0.25
0.25
0.25
 Chứng minh: PA.PO = PC.PM
Chứng minh được đồng dạng với (g.g)
Suy ra 
Suy ra PA.PO=PC.PM
0.25
0.25
Chứng minh E; F; P thẳng hàng.
Chứng minh được CA = CM = CF; DB = DM = DE
Gọi G là giao điểm của PF và BD, cần chứng minh G trùng E
Dựa vào AC//BD chứng minh được 
Suy ra DE = DG hay G trùng E.
Suy ra E; F; P thẳng hàng
0.25
0.25
Câu 5
(1 điểm)
 (; )
0.25
0.25
0.25
9x - 3 = 0 x = 1/3 (Thỏa mãn điều kiện)
Kết luận:
0.25
ĐỀ SỐ 4:
MA TRẬN ĐỀ KIỂM TRA 
 Cấp độ 
Các chủ đề 
Nhận Biết
Thông Hiểu
Vận Dụng 
Tổng cộng
Vận dụng thấp 
Vận dụng cao 
1.Hệ phương trình bậc nhất hai ẩn 
Giải hệ phương trình 
Số câu 1
Số điểm 1 – Tỉ lệ 10%
Số câu 1
Số điểm 1	 
Số câu 1
 1điểm =10% 
2.Hàm số và phương trình bậc nhất hai ẩn 
Vẽ đồ thị hàm số 
Giải phương trình trùng phương 
Tìm tọa độ giao điểm của (d ) và (P).
Vận dụng định lý Vi-ét
Giải bài toán bằng cách lập phương trình 
Số câu 5
Số điểm 5,5– Tỉ lệ55%
Số câu 1
Số điểm 1	 
Số câu 1
Số điểm 1	 
Số câu 2
Số điểm 2	 
Số câu 1
Số điểm 1,5	 
Số câu 5
5,5 điểm= 55%
3.Góc với đường tròn 
Chứng minh tứ giác nội tiếp được đường tròn 
Chứng minh hệ thức hình học 
Tính diện tích hình phẳng 
Số câu3
Số điểm 3,5– Tỉ lệ35%
Số câu 1
Số điểm 1,5	 
Số câu 1
Số điểm 1	 
Số câu 1
Số điểm 1	 
Số câu 3
3,5 điểm= 35%
Tổng số câu 9
Tổng số điểm 10
 Tỉ lệ 100%
Số câu 2
Số điểm 2,5
25%
Số câu 2
Số điểm 2 20%
Số câu 5
Số điểm 5,5
55%
Số câu 9
Số điểm 10 
ĐỀ KIỂM TRA 
Bài 1: ( 3 điểm) ( Không dùng máy tính cầm tay )
Giải hệ phương trình:
Giải phương trình:
Cho phương trình bậc hai:
	(m là tham số )
	Tìm m để phương trình có hai nghiệm thỏa mãn 
Bài 2: (1,5 điểm)
Một tam giác vuông có chu vi bằng 30m, cạnh huyền bằng 13m. Tính mỗi cạnh góc vuông.
Bài 3: ( 2 điểm)
Trong mặt phẳng tọa độ cho prabol( P): 
Vẽ đồ thị ( P )
Bằng phương pháp đại số tìm tọa độ giao điểm A và B của (P) và đường thẳng (d): 
Bài 4: (3,5điểm)
Từ điểm A ở ngoài đường tròn (0;2cm). Kẻ hai tiếp tuyến AB, AC và cát tuyến AMN với đường tròn đó (M nằm giữa A và N), cho góc BAC có số đo bằng 600. 
Chứng minh tứ giác ABOC nội tiếp đường tròn. Xác định tâm và bán kính của đường tròn ngoại tiếp tứ giác ABOC.
Chứng minh: 
Tính diện tích phần hình giới hạn bởi các đoạn AB, AC và cung nhỏ BC nói trên.
ĐÁP ÁN VÀ THANG ĐIỂM 
BÀI 
ĐÁP ÁN 
ĐIỂM
1.1
Giải hệ phương trình:
1đ
0,25đ
0,25đ
0,25đ
Vậy hệ phương trình có một nghiệm duy nhất 
0,25đ
1.2
Giải phương trình:
1đ
Đặt phương trình trở thành 
0,25đ
Giải và (nhận) (nhận)
0,25đ
0,25đ
Vậy phương trình có 4 nghiệm: 
0,25đ
1.3
Tìm m để phương trình có hai nghiệm thỏa mãn 
1đ
Phương trình có nghiệm khi D’
0,25đ
Viết đúng hệ thức Vi-et 
0,25đ
0,25đ
vậy m = 8
0,25đ
2 
Tìm hai cạnh góc vuông
1,5đ
Gọi là cạnh góc vuông thứ nhất. Điều kiện 
0,25đ
Cạnh vuông thứ hai: 
0,25đ
Sử dụng định lý Pitago viết phương trình 
0,25đ
0,25đ
Lập 
0,25đ
(nhận) (nhận)
Vậy độ dài hai cạnh góc vuông là: 12m và 5m 
0,25đ
3
a. Vẽ đồ thị (P): 
1đ
Bảng giá trị
-2
-1
0
1
2
-8
-2
0
-2
-8
0,5đ
Vẽ đúng đồ thị 
0,5đ
b.Tọa độ giao điểm của (P) và (d)
1đ
Phương trình hoành độ giao điểm của (P) và (d) là: 
0,25đ
Giải ra nghiệm 
0,25đ
Tìm được tọa độ giao điểm A(-1;-2) và B()
0,5đ
4
Vẽ hình:
. Tứ giác ABOC có (tính chất của tiếp tuyến )
0,5đ
 Tứ giác ABOC nội tiếp đường tròn 
0,5đ
(tính chất hai tiếp tuyến giao nhau ) và là tam giác đều 
(hai góc nội tiếp cùng chắn cung)
0,25đ
Vậy tứ giác ABOC nội tiếp trung đường tròn tâm là trung điểm của OA bán kính bằng 2 cm.
0,25đ
Xét hai tam giác .
 (góc tạo bởi tia tiếp tuyến và góc nội tiếp cùng chắn cung )
0,25đ
chung 
0,25đ
Suy ra DABM đồng dạng DANB(g.g)
0,25đ
0,25đ
Tứ giác ABOC nội tiếp 
0,25đ
 Squạt OBMC 
0,25đ
0,25đ
Scần tìm = SOBAC – Squạt 
0,25đ
Học sinh giải cách khác đúng vẫn đạt điểm tối đa
ĐỀ SỐ 5:
MA TRẬN ĐỀ KIỂM TRA:
 Cấp độ
Chủ đề
Nhận biết
Thông hiểu
Vận dụng
Cộng
Cấp độ thấp
Cấp độ cao
Hàm số y = ax2
Vẽ được đồ thị hàm số
Số câu 	
Số điểm
Tỉ lệ
1(1b)
1đ
10%
1
1đ
10%
Hệ phương trình và phương trình bậc hai.
Xác định hệ số, điều kiện để một PT là phương trình bậc hai một ẩn.
Giải phương trình bậc hai, hệ phương trình bậc hai.
Tìm giá trị tham số theo điều kiện của nghiệm
Số câu 
Số điểm
Tỉ lệ
1(2a)
1đ
10%
2(1a,2b)
2đ
20%
1(2c)
1đ
10%
4
4 đ
40%
Giải bài toán bằng cách lập hệ phương trình, phương trình.
Lập được bài phương trình bậc hai dựa trên đề bài. Từ đó giải được bài toán thực tế
Số câu 
Số điểm
Tỉ lệ
1(3)
2đ
20%
1
2 đ
20%
Góc với đường tròn.Tứ giác nội tiếp.
Vận dụng được tính chất về góc với đường tròn.
Chứng minh được tứ giác nội tiếp đường tròn
Số câu 
Số điểm
Tỉ lệ
2(5a,5b)
2đ
20%
2
2 đ
20%
5. Hình trụ, hình nón, hình cầu.
Vận dụng tốt công thức tính diện tích Xq, thể tích của hình trụ
Số câu 
Số điểm
Tỉ lệ
3(4a,b)
1đ
10%
1
1 đ
20%
Tổng số câu
Tổng số điểm
Tỉ lệ %
1
1đ
10%
5
4đ
40%
3
4đ
40%
1
1đ
10%
10
10 đ
100%
ĐỀ KIỂM TRA
I. PHẦN CHUNG
Bài 1. (2,0 điểm)
 Giải hệ phương trình và phương trình sau:
a) 	b) 4x4 + 9x2 - 9 = 0
Bài 2. (1,0 điểm)
Cho parabol (P): y = x2 và đường thẳng (d): y = 2x+3 
a) Vẽ (P).
b) Xác định giao điểm (P) và (d) bằng phép toán.
Bài 3. (2,0điểm)
 Cho phương trình: x2 + 2(m – 1)x + m2 – 3 = 0 (1) (m là tham số)
a) Giải phương trình (1) với m = 2
b) Tìm m để phương trình (1) có hai nghiệm x1; x2 thỏa mãn x12 + x22 = 52
 Bài 4. (1,0 điểm) Giải bài toán bằng cách lập hệ phương trình:
 	Tìm số tự nhiên có hai chữ số biết chữ số hàng đơn vị lớn gấp ba lần chữ số hàng chục và nếu đổi chỗ các chữ số cho nhau thì được số mới lớn hơn số ban đầu 18 đơn vị
Bài 5. (3,0 điểm) 
Cho nửa đường tròn (O) đường kính AB. Điểm M nằm trên nửa đường tròn 
(M ≠ A và B). Tiếp tuyến tại M cắt tiếp tuyến tại A và B của đường tròn (O) lần lượt tại C và D.
Chứng minh rằng: tứ giác ACMO nội tiếp.
Chứng minh rằng: 
Gọi P là giao điểm CD và AB. Chứng minh: PA.PO = PC.PM
Gọi E là giao điểm của AM và BD; F là giao điểm của AC và BM. 
Chứng minh: E; F; P thẳng hàng.
 Bài 6. (1,0 điểm) 
	Cho ΔABC vuông tại A. Cạnh AB = 3 cm; AC= 4 cm. Quay ΔABC một vòng quanh cạnh AC . Vẽ hình, tính diện tích xung quanh và thể tích của hình được sinh ra?
--- Hết ---
ĐÁP ÁN, BIỂU ĐIỂM
Bài 1: (2 điểm) Giải phương trình, hệ phương trình sau:
a. b. 4x4 + 9x2 - 9 = 0
a)1 đ b) 1 đ 
a. 
Vậy hệ phương trình có 1 nghiệm (x=3; y=1)
b. 4x4 + 9x2 - 9 = 0 (1)
Đặt t=x2 ()
Với 
Vậy phương trình (1) có 2 nghiệm 
(1 điểm)
(0,5 điểm)
(0,5 điểm)
Bài 2: (1 điểm) Cho parabol (P): y = x2 (P) và đường thẳng (d): y = 2x+3
Vẽ (P).
Xác định giao điểm (P) và (d) bằng phép toán.
 a)0,5 đ b) 0,5 đ 
a. Vẽ (P). Bảng giá trị: 
x
-2
-1
0
1
2
y=x2
4
1
0
1
4
Vẽ đúng:
b. Phương trình hoành độ giao điểm (d) và (P)
x2 = 2x + 3
Với x = -1 y = 1 P(-1; 1)
Với x = 3 y = 9 Q(3; 9)
Vậy (d) cắt (P) tại hai điểm phân biệt P(-1; 1); Q(3; 9).
(0,5 điểm)
(0,5 điểm)
Bài 3: (2điểm) Cho phương trình:
x2 + 2(m – 1)x + m2 – 3 = 0 (1) (m là tham số)
Giải phương trình với m = 2
Tìm m để phương trình (1) có hai nghiệm x1; x2 thỏa mãn x12+x22 = 52
a)1 đ b) 1 đ 
a. Với m = 2 pt(1): x2 + 2x + 1 = 0
	Phương trình có nghiệm kép x1 = x2 = -1
b. Tìm m để phương trình 1 có hai nghiệm x1; x2 thỏa mãn x12+x22 = 52
	x2 + 2(m – 1)x + m2 – 3 = 0 (1) (m là tham số)
a = 1; b’= (m – 1) ; c = m2 – 3
∆’=b’2 – a.c = (m – 1)2 – (m2 – 3) = –2m + 4
Phương trình (1) có hai nghiệm x1, x2 khi ∆’≥0 –2m + 4 ≥0m≤2
Với m ≤ 2 phương trình (1) có hai nghiệm x1, x2 . Áp dụng hệ thức Vi-ét ta có:
x1 + x2 = –2(m – 1)
x1 . x2 = m2 – 3
Ta có: 
	Vậy với m = –3 thì phương trình 1 có hai nghiệm x1; x2 thỏa mãn x12+x22=52
(1 điểm)
(0,5 điểm)
(0,5 điểm)
Bài 4 (1 điểm:Giải bài toán bằng cách lập hệ phương trình:
 Tìm số tự nhiên có hai chữ số biết chữ số hàng đơn vị lớn gấp ba lần chữ số hàng chục và nếu đổi chỗ các chữ số cho nhau thì được số mới lớn hơn số ban đầu 18 đơn vị
Gọi chữ số hàng chục là x, chữ số hàng đơn vị là y. 
Số ban đầu là 10x + y; số mới 10y + x
Theo đề ta có : y = 3x
 10y + x – ( 10x + y ) = 18 
Ta có hệ phương trình 
Giải được x = 1 , y = 3 ( thỏa mãn điều kiện )
(0,5 điểm)
(0,5 điểm)
Bài 5:(3 điểm) Cho nửa đường tròn (O) đường kính AB. Điểm M nằm trên nửa đường tròn (M≠A;B). Tiếp tuyến tại M cắt tiếp tuyến tại A; B của đường tròn (O) lần lượt tại C và D.
Chứng minh rằng: tứ giác ACMO nội tiếp.
Chứng minh rằng: 
Gọi P là giao điểm của CD và AB. Chứng minh: PA.PO = PC.PM
Gọi E là giao điểm AM và BD; F là giao điểm của AC và BM. Chứng minh E; F; P thẳng hàng.
Hình vẽ: 0,5đ a)0,5 đ b) 1 đ c) 0,5đ d) 0,5đ
GT; KL, hình vẽ 
Tứ giác ACMO nội tiếp.
Chứng minh được tứ giác ACMO nội tiếp
Chứng minh rằng: 
- Chứng minh được 
- Chứng minh tứ giác BDMO nội tiếp
- Chứng minh được 
Suy ra 
Chứng minh: PA.PO = PC.PM
Chứng minh được đồng dạng với (g.g)
Suy ra Suy ra PA.PO=PC.PM
 Chứng minh E; F; P thẳng hàng.
Chứng minh được CA = CM = CF; DB = DM = DE
Gọi G là giao điểm của PF và BD, cầm chứng minh G trùng E
Dựa vào AC//BD chứng minh được 
Suy ra DE = DG hay G trùng E.
Suy ra E; F; P thẳng hàng
(0,5 điểm)
(0,5 điểm)
(0,5 điểm)
(0,5 điểm)
(0,5 điểm)
(0,5 điểm)
Bài 6: (1 điểm) Cho ΔABC vuông tại A. Cạnh AB = 3 cm; AC= 4 cm. Quay ΔABC một vòng quanh cạnh AC .
Tính diện tích xung quanh và thể tích của hình được sinh ra ?
	Vẽ đúng hình.
b) Tính diện tích xung quanh và thể tích của hình được sinh ra?
Tính được BC = 5
Tính được 
 Tính được 
(0,25 điểm)
(0,25 điểm)
(0,25 điểm)
(0,25 điểm)
Học sinh làm cách khác đúng vẫn cho điểm tối đa câu đó
ĐỀ SỐ 6:
MA TRẬN ĐỀ KIỂM TRA
 Cấp độ
Tên 
Chủ đề
Nhận biết
Thông hiểu
Vận dụng
Cộng
Chủ đề 1
Hệ phương trình
Biết giải hệ phương trình bằng phương pháp cộng hoặc phương pháp thế.
Số câu
Điểm
Tỉ lệ
1
1
10%
1
1
10%
Chủ đề 2
Ph/ trình bậc hai
Biết giải phương trìng bậc hai bằng công thức nghiệm
Số câu
Điểm
Tỉ lệ
1
1
10%
1
1
10%
Chủ đề 3
Hệ thức vi-ét
Sử dụng vi-ét để chứng tỏ pt có nghiệm 
Vận dụng vi-ét lập phương trình bậc hai biết trước quan hệ các nghiệm
Số câu
Điểm
Tỉ lệ
1
0,5
5%
1
1,5
15%
2
2
20%
Chủ đề 4
Hàm số đồ thị
Biết vẽ đồ thị hàm số y=ax2.
Xác định đúng tọa độ giao điểm hai đồ thị 
Số câu
Điểm
Tỉ lệ
1
1
10%
1
1
10%
2
2
20%
Chủ đề 5
Hình học
Nhận biết tứ giác nội tiếp
Dùng tính chất TGNT, tính chất đối xứng để chứng minh tam giác cân, quan hệ vuông góc.
Vận dụng tính chất TGNT để chứng minh 3 điểm thẳng hàng
Số câu
Điểm
Tỉ lệ
1
1
10%
2
2
20%
1
1
10%
4
4
40%
T. Số câu
T. Điểm
Tỉ lệ
4
4
40%
4
4
40%
2
2
20%
10
10
100%
ĐỀ KIỂM TRA
Bài 1: ( 2,0 điểm) ( Học sinh không dùng máy tính cầm tay)
	a) Giải phương trình: x2 - 3x - 10 = 0
	b) Giải hệ phương trình: 
Bài 2: (2,0 điểm)
	Cho phương trình bậc hai 2x2 – mx + m - 2 = 0 ( m là tham số)
Chứng tỏ phương trình luôn có nghiệm với mọi giá trị của m
Lập phương trình bậc hai có hai nghiệm là y1; y2 biết và 
Bài 3: ( 2,0 điểm)
	Cho hàm số y = 2x2 (P)
Vẽ đồ thị của (P)
Tìm tọa độ giao điểm của (P) và đường thẳng y = 3 – x 
Bài 4: ( 4,0 điểm)
	Cho đường tròn tâm O, vẽ hai dây cung AB và CD vuông góc với nhau tại M trong đường tròn (O). Qua A kẻ đường thẳng vuông góc BC tại H và cắt đường thẳng CD tại E. Gọi F là điểm đối xứng của C qua AB. Tia AF cắt BD tại K. Chứng minh:
Tứ giác AHCM nội tiếp.
Tam giác ADE cân.
AK vuông góc BD.
H, M, K thẳng hàng.
---------- Hết ----------
Hướng dẫn chấm và biểu điểm 
BÀI
CÂU
NỘI DUNG
ĐIỂM
1
a
- Lập đúng 
- Tính đúng x1
- Tính đúng x2
0,5
0,25
0,25
b
HPT 
ó 
ó 
ó 
0,25
0,25
0,25
0,25
2
a
- Tính được a + b + c = 2 + (– m) + m – 2 = 0
- Kết luận pt có nghiệm với mọi giá trị của m
0,25
0,25
b
- Tính đúng 
- Biến đổi 
- Phương trình cần tìm là: 
0,25
0,25
0,25
0,25
0,25
0,25
3
a
- Lập bảng đúng
- Vẽ đồ thị đúng
0,5
0,5
b
- Lập đúng phương trình hoàng độ giao điểm: 2x2 = 3 - x
- Giải pt tìm được x1=1; x2 = 
- Thay vào hàm số (P) tìm được y1=2 ; y2 = 
- Kết luận tọa độ giao điểm ( 1; 2) và (; )
0,25
0,25
0,25
0,25
4
a
- Xét tứ giác AHCM có:
 (gt)
Suy ra 
Vậy AHCM nội tiếp
0,5
0,25
0,25
b
- Từ AHCM nội tiếp suy ra: (cùng bù )
Mà ( cùng chắn )
Nên 
-ADE có AM DE và nên ADE cân tại A
0,25
0,25
0,25
0,25
c
- F là đối xứng của C qua AB => CBF cân tại B
=> 
- Gọi N là giao điểm BF với AD ta có: AHB = ANB ( g-c-g)
=> 
-ADB có DM và BN là hai đường cao nên F là trực tâm
=> AF BD hay AK BD.
0,25
0,25
0,25
0,25
d
- Tứ giác AHBK nội tiếp ( )=> 
- Tứ giác FMBK nội tiếp ( ) => 
- Mà ( FBC cân tại B) nên 
- Suy ra: K, M, H thẳng hàng.
0,25
0,25
0,25
0,25
Các cách giải khác nếu đúng vẫn cho điểm tối đa cho từng câu.
ĐỀ SỐ 7:
MA TRẬN ĐỀ
Cấp độ
Chủ đề
Nhận biết
Thông hiểu
Vận dụng
Cộng
Cấp độ thấp
Cấp độ cao
1. Hệ phương trình bậc nhất một ẩn
Giải hệ phương trình
Viêt phương trình đường thẳng 
Số câu 
Số điểm 
Tỉ lệ %
1
1
1
1
2
2
20%
2. Hàm số y = ax2 ( a ≠ 0 ) 
 Vẽ đồ thị
Số câu 
Số điểm 
 Tỉ lệ %
1
1
1
1
10%
3. Phương trình bậc hai một ẩn -Hệ thức Vi-et.
 Biết giải PT trùng phương
Vận dụng định lý Vi-et để tìm nghiệm còn lại. 
-Vận dụng định lý Vi-et vào điều kiện về nghiệm cho trước của pt bậc 2 
Số câu 
Số điểm 
Tỉ lệ %
1
1,0
1
1,0
1
1,0
3
 3,0
30%
4. Góc với đường tròn
Tính số đo góc +vẽ hình đúng
- Vẽ hình 
- Ch/m tứ giác nội tiếp
Vận dụng các đ/lí về góc để ch/m tam giác cân 
Chứng minh hệ thức 
Số câu 
Số điểm 
Tỉ lệ %
1
1,0
1
1,0
1
1,0
1
1,0
4
4,0
40%
Tổng số câu 
Tổng số điểm Tỉ lệ %
1
1
10%
4
4
40%
 5
 5 
 50 % 
10
10
100%
ĐỀ KIỂM TRA
Câu 1: ( 2,0đ) 
 Giải hệ phương trình 
Giải phương trình : 
Câu 2: (2,0đ)
 Cho hàm số y = - x2 có đồ thị (P)
Vẽ đồ thị (P) của hàm số .
Trên (P) lấy hai điểm M, N lần lượt có hoành độ là - 1 và 2.Viết phương trình đường thẳng M N.
Câu 3 : (2,0đ) Cho phương trình bậc hai ẩn x : 
 x2 + mx + 2m – 4 = 0 (1) 
a) Biết phương trình có một nghiệm x1 = 3. Hãy tính nghiệm còn lại x2 và m .
b) Gọi x1, x2 là hai nghiệm phân biệt của phương trình (1). 
Tìm giá trị nguyên dương của m để biểu thức có giá trị nguyên.
 Câu 4 : (4,0đ) 
Từ điểm M ở bên ngoài đường tròn (O; R) vẽ hai tiếp tuyến MA, MB ( A, B là các tiếp điểm). Gọi E là điểm nằm giữa M và A. Đường tròn ngoại tiếp tam giác AOE cắt AB tại điểm H. Nối EH cắt MB tại F.
Tính số đo góc EHO
Chứng minh rằng tứ giác OHBF nội tiếp 
Chứng minh rằng tam giác EOF cân
Gọi I là trung điểm của AB. Chứng minh rằng OI. OF = OB.OH 
−−−−−−−−−−−−−−−−−−−−−−−−−−HẾT−−−−−−−−−−−−−−−−−−−−−−−−−−−
ĐÁP ÁN – HƯỚNG DẪN CHẤM
Câu
Nội dung
Điểm
1 
(2,0đ) 
a) 
 Giải đúng x=1; y=1 
0,5điểm
0,5điểm 
b) Đặt t = x2; ta có pt: t2 - 7t - 8 = 0
Tính đúng D , hoặc nhẩm nghiệm a+b+c =0 
 Tính đúng hai nghiệm t1 = -1(loại ), t2 =- c /a = 8 ( nhận )
 Tính đúng 
0,25điểm
0,25điểm
0,25điểm
0,25điểm
2
(2,0đ)
a) Lập đúng bảng giá trị 
 Vẽ đúng đồ thị 
0,5 điểm 
0,5điểm
b)Tìm được : M(-1; -1/2), N(2; -2)
Lập luận tìm được phương trình đường thẳng MN : 
y = -0,5x - 1 
0,5điểm
0,5 điểm 
3
(2,0đ)
a) Thay x = 3 vào phương trình tìm được :9 + 3m + 2m-4=0
 m=-1
Áp dụng hệ thức vi –et : 
 Tính được =- 2 
0,25điểm
0,25điểm
0,25điểm
0,25điểm
 b).Tính đúng ∆ 
Để phương trình có nghiệm thì ∆ ≥ 0 => với mọi m phương trình luôn có nghiệm
Áp dụng Vi-et : 
 Tìm được ( sau khi đ/c đk ) 
0,25điểm
0,25điểm
0,25điểm
0,25điểm
5
(4,0đ)
Hình vẽ đúng 
0,5điểm
a) Lí luận được 
0,5điểm
b) Lí luận được 
suy ra được tứ giác OHBF nội tiếp
0,5điểm
0,5điểm
c)( cùng chắn cung OH của đường tròn đường kính OE)
( ∆ AOB cân)
( cùng chắn cung OH của đường tròn đường kính OF)
S
Suy ra hay ∆ OEF cân tại O
0,25điểm
0,25điểm
0,25điểm
0,25điểm
d) Chứng minh được ∆ OIB ∆ OHF 
Suy ra nên OI.OF = OB.OH
0,5điểm
0,5điểm
ĐỀ SỐ 8:
MA TRẬN ĐỀ
Tên Chủ đề
(nộidung,chương)
Nhận biết
Thông hiểu
Vận dụng
Vận dụng ở mức cao hơn
Tổng
Hệ phương trình bậc nhất hai ẩn 
Biết cách giải hệ pt bậc nhất hai ẩn
Số câu
Số điểm 
 Tỉ lệ %
1
	1.0
10%
1
1.0
 10%
Hàm số y = ax2 (a.
Phương trình bậc hai
Vận dụng được giải pt qui về phương trình bậc hai
Biết vẽ đồ thị hàm số y=a.x2(a
Tìm tọa độ giao điểm của parabol và đường thẳng
Tìm giá trị của tham số để hai nghiệm thỏa mãn đẳng thức đối xứng của hai nghiệm.
Số câu 
Số điểm 
Tỉ lệ %
3
3.0
30%
1
	1.0
10%
4
4.0
40%
Bài toán phương trình bậc hai
Vận dụng bài toán thực tế dạng chuyển động
Số câu 
Số điểm 
Tỉ lệ %
1
	1.5
15%
1
1.5 
15%
Góc và đường tròn
Chứng minh tứ giác nội tiếp
Thấy được sự liên hệ các loại góc của đường tròn. Hệ thức về cạnh và góc trong tam giác vuông
Số câu 
Số điểm 
Tỉ lệ %
1
1.25
12,5%
2
1.5
15%
3
2.75
27.5%
Hình nón - hình cầu
Hiểu các công thức tính diện tích, thể tích
Vận dụng công thức tính
Số câu 
Số điểm 
Tỉ lệ %
1
0.25
2,5%
1
0.5
5%
2
0.75
7,5%
Tổng số câu 
Tổng số điểm
Tỉ lệ %
1
0.25
2.5%
2
2.25
22.5%
8
 7.5
 75%
11
 10.0
 100%
 ====================================
ĐỀ THI HỌC KỲ II 
Bài 1: ( 2,0 điểm)
Giải các phương trình và hệ phương trình sau: 
	 a) x4 -3x2 – 4 = 0 	 b) 
Bài 2: (1 điểm)
 Cho phương trình (ẩn số x): x2 -2x +2m -1 = 0 (1). Tìm giá trị của m để phương trình (1) có 2 nghiệm x1, x2 và 
Bài 3: ( 2,0 điểm) Trong mặt phẳng Oxy cho (P) y = x2 và đường thẳng (d): y = -2x + 3 
	a) Vẽ đồ thị của (P) 
 b) Tìm tọa độ giao điểm của (P) và (d) bằng phép tính. 
Bài 4: (1,5 điểm) Khoảng cách giữa hai bến sông A và B là 30km, một canô đi từ bến A đến bến B, nghỉ 40 phút ở bến B rồi quay lại bến A. Kể từ lúc khởi hành đến khi về tới bến A hết tất cả 6 giờ. Hãy tìm vận tốc canô khi nước yên lặng, biết vận tốc của nước chảy là 3km/h. 
Bài 5: (3,5 điểm) Cho nửa đường tròn (O; R), đường kính AB, Gọi C là điểm chính giữa của cung AB. Lấy M thuộc cung BC sao cho AM cắt OC tại N và MB = MN. 
	a) Chứng minh: Tứ giác OBMN nội tiếp. 
	b) Chứng minh: . Từ đó tính số đo 
 c) Tính độ dài cạnh ON. 
	d) Tính thể tích của hình được sinh ra khi quay tam giác AON quanh AO. 
================hết =============
Đáp án và hướng dẫn chấm:
Bài
Nội dung
Điểm
Bài 1.a/ 
(1,0 điểm)
Ta đặt t = x2 (điều kiện t)
0,25
Phương trình trở thành t2 - 3t – 4 = 0
0,25
Tìm được t = 4 và t = -1(loại)
0,25
Tìm được x1 = -2 và x2 = 2
0,25
Bài 1.b/
(1,0 điểm)
Giải hệ pt: 
0,25
0,5
Hệ phương trình có nghiệm duy nhất: (3; -1)
0,25
Bài 2
(1,0 điểm)
Tính được ’= -2m + 2và tìm được: 
0,25
Theo Vi-et : x1 + x2 = 2 và x1 . x2 = 2m – 1
0,25
Tính được 
0,25
Tính được: 
0,25
Bài 3
(2,0 điểm)
1/Lập được 5 điểm thuộc đồ thị bằng bảng giá trị :
x
-2
-1
0
1
2
y = x2
4
1
0
1
4
0,5
Vẽ đúng chính xác 
0,5
2/Phương trình hoành độ giao điểm của (d) và (P): x2 +2x -3= 0 
và giải được x1 = 1 và x2 = -3
0,25
0,5
Tìm được 2 điểm (1;1) và (-3; 9)
0,25
Bài 4
(1,5 điểm)
Gọi vận tốc canô khi nước yên lặng là x (km/h), x > 3
0,25
Vận tốc xuôi dòng là x + 3 (km/h)
Vận tốc ngược dòng là x – 3 (km/h)
Thời gian canô xuôi dòng là (h)
Thời gian ca nô ngược dòng là (h)
0,25
0,25
Theo đề bài ta có pt: 
0,25
Giải được: x1 = 12 ; x2 = (loại)
Trả lời: Vận tốc ca nô khi nước yên lặng là 12km/h.
0,25
0,25
Bài 5
(3,5 điểm)
FHình vẽ đúng
a/ Nêu được 
 và 
 Suy ra Tứ giác OBMN nội tiếp.
0,5
0,5
0,25
b/ Nêu được: ( cùng chắn cung MB)
-Nêu được ( Góc nội tiếp và góc ở tâm cùng chắn cung MB)
- suy ra 
-∆MBN có MB = MN (gt) , ( Góc nội tiếp chắn nửa đường tròn). Nên ∆ MBN vuông cân tại M . 
Suy ra 
- và tính được : 
0,25
0,25
0,25
0,25
0,25
0,25
c/ ON = OA tanA
 ON = R tan 22030’
0,25
d/ Viết được V = 
 Tìm được V = 
 V = (đvtt)
0,25
0,25
F Mọi cách làm đúng khác của học sinh vẫn nhận đầy đủ số điểm tương ứng
ĐỀ SỐ 9:
Ma trận
Cấp độ
Chủ đề
Nhận biêt
Thông hiểu
Vận dụng
Cộng
Thấp
Cao
1. Hệ hai pt bậc nhất hai ẩn
Vận dụng được các bước giải toán bằng cách lập hệ phương trình b/ nhất 2 ẩn
Số câu
1
1
Số điểm 
Tỉ lệ
1,5
15%
1,5 
15%
2. Hàm số
y = ax2
( a 0) , Phương trình bậc hai 1 ẩn
Trình bày được giải phương trình bậc 2
Vẽ được đồ thị hàm số. Giải thích được điều kiện để phương trình bậc 2 có nghiệm. Tìm tọa độ giao điểm của hàm số bậc 2 với đường thằng 
y = ax +b
Vận dụng hệ thức Viet tìm điều kiện thỏa mãn yêu cầu đề bài
Số câu
1
3
1
5
Số điểm 
Tỉ lệ
1
10%
3
30%
1
10%
5
50%
3.Đường tròn, góc với đt, tứ giác nội tiếp...
Vẽ hình. Trình bày được tứ giác nội tiếp
Chứng minh được 2 biểu thức tích bằng nhau thông qua việc chứng minh 2 tam giác đồng dạng
Biết cách tìm độ dài đường thẳng thông qua chứng minh tam giác đồng dạng để tìm điều kiện thõa mãn yêu cầu đề bài
Số câu
2