Đềkiểm tra học kì I môn: Toán 7

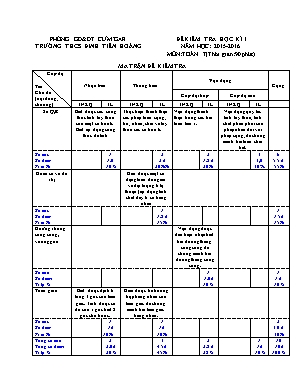
PHÒNG GD&ĐT CƯM’GAR
TRƯỜNG THCS ĐINH TIÊN HOÀNG
ĐỀKIỂM TRA HỌC KÌ I
NĂM HỌC: 2015-2016
MÔN:TOÁN 7(Thời gian:90 phút)
MA TRẬN ĐỀ KIỂM TRA
 Cấp độ
Tên 
Chủ đề 
(nội dung,
chương)
Nhận biết
Thông hiểu
Vận dụng
Cộng
Cấp độ thấp
Cấp độ cao
TNKQ
TL
TNKQ
TL
TNKQ
TL
TNKQ
TL
Số Q,R
Biết được các công thức tính lũy thừa của một số hữu tỉ.
Biết áp dụng công thức để tính
Thực hiện thành thạo các phép toán cộng, trừ, nhân, chia và lũy thừa các số hữu tỉ.
Vận dụng thành thạo trong các bài toán tìm x.
Vận dụng quy tắc tính lũy thừa, tính chất phân phối của phép nhân đối với phép cộng, để chứng minh bài toán chia hết.
Số câu 
Số điểm 
Tỉ lệ %
1
1,0
10%
2
2 đ
20%%
2
1,5 đ
20%
1
1,0
10%
6
5,5 đ 
55%
Hàm số và đồ thị
Giải được một số dạng toán đơn giản về đại lượng tỉ lệ thuận (áp dụng tính chất dãy tỉ số bằng nhau
Số câu 
Số điểm 
Tỉ lệ %
1
1,5 đ
15%
1
1,5đ 
15%
Đường thẳng song song, vuông góc
Vận dụng được dấu hiệu nhận biết hai đường thẳng song song để chứng minh hai đường thẳng song song.
Số câu 
Số điểm 
Tỉ lệ %
1
1,0đ
10%
1
1 đ
10%
Tam giác
Biết được định lí tổng 3 góc của tam giác. Tính được số đo của 1 góc biết 2 góc cho trước.
Hiểu được ba trường hợp bằng nhau của tam giác để chứng minh hai tam giác bằng nhau. 
Số câu 
Số điểm 
Tỉ lệ %
1
1đ
10%
1
1đ
10%
3
3,0 đ
30%
Tổng số câu 
Tổng số điểm
Tỉ lệ %
2
2,0đ
20%
4
4,5đ
45%
3
3,5 đ
35%
1
1đ
10%
10
10đ 
100%
Trường THCS Đinh Tiên Hoàng 
Họ, tên:
Lớp: 
KIỂM TRA HỌC KỲ I (2015-2016)
MÔN: TOÁN 7
Thời gian: 90 phút
 ĐỀ:
 I. Lý thuyết
Câu 1: (1 điểm) Viết công thức tính lũy thừa của một tích. 
 	Áp dụng tính: . 35
Câu 2: (1 điểm) Phát biểu định lí tổng ba góc của một tam giác. 
Áp dụng : Cho tam giác ABC có Â = 550, = 700, tính ?
II. Bài tập
Câu 1: (2 điểm) Thực hiện các phép tính (bằng cách hợp lý nếu có thể): 
a) 	b) . - .
Câu 2: (1,5 điểm) Tìm x biết: 
a) 	b) 
Câu 3: (1,5 điểm) 
	 Cho tam giác có số đo các góc lần lượt tỉ lệ thuận với 3; 5; 7. Tính số đo các góc của tam giác đó.
Câu 4: (2 điểm) Cho DABC có AB = AC. M trung điểm của BC. 
a) Chứng minh rằng: D AMB = D AMC . 
b)Trên tia đối của tia MA lấy điểm D sao cho MA = MD. Chứng minh rằng AB // CD. 
Câu 5:( 1điểm)
Cho với . Chứng minh rằng A chia hết cho 6.
BÀI LÀM:
........................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................ ...................................................................................................... .........................
PHÒNG GD&ĐT CƯM’GAR
TRƯỜNG THCS ĐINH TIÊN HOÀNG
ĐỀKIỂM TRA HỌC KÌ I
NĂM HỌC:2015-2016
MÔN:TOÁN 7 (Thời gian:90 phút)
ĐÁP ÁN VÀ HƯỚNG DẪN CHẤM
CÂU
NỘI DUNG
ĐIỂM
I
LÝ THUYẾT
1
Công thức tính lũy thừa của một tích: (x . y)n = xn. yn
Áp dụng: . 35 = 
0,5
0,5
2
Tổng ba góc của một tam giác bằng 1800
Xét có: < A + < B + < C = 1800
 550 + < B + 700 = 1800
 < B = 1800 – (550 +700) = 550
0,5
0,25
0,25
II
BÀI TẬP
1
a)
 b) . - .=.(-) 
 = - 
0,5
0,5
0,5
0,5
2
a)
b)	
 hoặc 
0,5
0,25
0,25
0,25
0,25
0,25
0,25
3
Gọi số đo các góc của tam giác lần lượt là x, y, z. ( x, y, z > 0)
Theo đề bài ta có: và x + y + z = 1800 (tổng ba góc trong tam giác)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
 x = 3.120 = 360
 y = 5.120 = 600
 z =7.120 = 840 
Vậy số số các góc của tam giác lần lượt là: 360 , 600 , 840
0,25
0,5
0,5
0,25
4
GT
AB = AC
M là trung điểm của BC
MA = MD
KL
a) 
b) AB // CD
a ) Xét ∆AMB và ∆AMC ta có:
AB = AC (gt)
MB = MC ( M là trung điểm của BC)
AM là cạnh chung.
 ∆AMB = ∆AMC (c-c-c)
b) Xét ∆MAB và ∆MDC ta có: 
MB = MC ( Chứng minh trên)
Góc M1= góc M2 ( Đối đỉnh)
MA = MD ( gt)
Do đó: ∆MAB = ∆MDC ( c- g – c)
 góc MAB = góc MDC ( hai góc tương ứng)
mà hai góc này ở vị trí so le trong 
 AB //CD.
0,5
0,75
0,5
0,25
5
Nên 
Vậy A với mọi 
0,25
0,25
0,25
0,25
Ngày, ./12/2015
Chuyên môn
Ngày, ./12/2015
Tổ trưởng
Ngày, 04 /12/2015
Người ra đề