Đề tuyển sinh thử vào lớp 10 năm học 2015 - 2016 môn: Toán - thời gian 120 phút

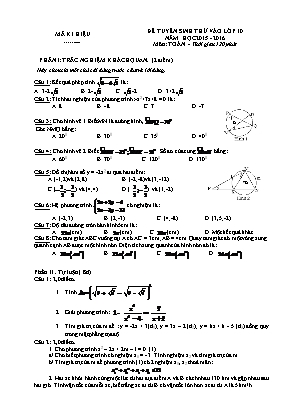
MÃ KI HIỆU
...........
ĐỀ TUYỂN SINH THỬ VÀO LỚP 10
NĂM HỌC 2015 - 2016
Môn: TOÁN - Thời gian 120 phút
 PHẦN I: TRẮC NGHIỆM KHÁCH QUAN. (2 điểm)
 Hãy chọn chỉ một chữ cái đứng trước câu trả lời đúng.
Câu 1: Kết quả phép tính là:
A. 3-2	 B. 2- 	 C. -2	 D. 3+2
Câu 2: Tích hai nghiệm của phương trình: -x2+7x+8 = 0 là:
o
	A. 8	 B. - 8	 C. 7	D. -7
Câu 3: Cho hình vẽ 1.Biết MN là đường kính, .
 Góc NMQ bằng:
	A. 200	 B. 300	 C. 350	D. 400
Câu 4: Cho hình vẽ 2. Biết . Số đo của cung bằng:
A. 600	 B. 700	 C. 1200	 D. 1300
o
Câu 5: Đồ thị hàm số y = -2x2 đi qua hai điểm:
 A.(-1;2) và (2;8)	 B. (-2;-8) và (3;-12) 
 C.() và (4;4)	 D.( ) và (1;-2)
Câu 6: Hệ phương trình có nghiệm là: 
	A. (-2;3)	B. (2;-3)	C. (4;-8)	 D. (3,5;-2)
Câu 7: Độ dài đường tròn bán kính 5cm là:
	A. (cm)	B. (cm) C. (cm)	 D. Một kết quả khác
Câu 8: Cho tam giác ABC vuông tại A có AC = 3cm; AB = 4cm. Quay tam giác đó một vòng xung quanh cạnh AB được một hình nón. Diện tích xung quanh của hình nón đó là: 
	A. 	B. 	C. 	D. 
Phần II . Tự luận ( 8đ)
Câu 1: 2,0 điểm.
Tính 
Giải phương trình : .
Tìm giá trị của m để : y = -2x + 3(d1); y = 3x – 2 (d2); y = kx + k - 5 (d3) đồng quy trong mặt phẳng tọa độ .
Câu 2: 2,0 điểm.
 1. Cho phương trình x2 – 2x + 2m – 1 = 0. (1)
 a/ Cho biết phương trình có nghiệm x1 = - 3. Tính nghiệm x2 và tìm giá trị của m.
 b/ Tìm giá trị của m để phương trình (1) có 2 nghiệm x1, x2 thoả mãn: 
 2. Hai xe khởi hành cùng một lúc từ hai địa điểm A và B cách nhau 130 km và gặp nhau sau hai giờ. Tính vận tốc của mỗi xe, biết rằng xe đi từ B có vận tốc lớn hơn xe đi từ A là 5 km/h.
Bài 4: 
Cho đường tròn (O;R), đường kính AB cố định và CD là một đường kính thay đổi không trùng với AB. Tiếp tuyến của đường tròn (O;R) tại B cắt các đường thẳng AC và AD lần lượt tại E và F.
1. Chứng minh rằng BE.BF = 4R2.
2. Chứng minh tứ giác CEFD nội tiếp đường tròn.
3. Gọi I là tâm đường tròn ngoại tiếp tứ giác CEFD. Chứng minh rằng tâm I luôn nằm trên một đường thẳng cố định.
Câu 4( 1 điểm).
 Cho các số dương x, y, z thỏa mãn xyz - 
Tìm giá trị nhỏ nhất của biểu thức P = (x+y)(x+z)
HƯỚNG DẪN CHẤM
Phần I : Trắc nghiệm ( 2đ) mỗi câu đúng 0,25đ
Ccâu
1
2
3
4
5
6
7
8
Đáp án 
D
A
A
D
C
D
A
B
Phần II: Tự luận (8,0 Điểm). 
Câu
Đáp án
Điểm
1
(2 điểm)
1) 	
0,25
0,25
2) (ĐK : ).
Đối chiếu với điều kiện kết luận phương trình có nghiệm duy nhất 
0,25
0,25
0,25
3. Hai đường thẳng (d1) và (d2) có hệ số x khác nhau nên hai đường thẳng (d1) và (d2) cắt nhau tại điểm M trong mặt phẳng tọa độ . Khi đó tọa độ của điểm M phải thỏa mãn : 
 Suy ra tọa độ của điểm M là M(1;1)
Để ba đường thẳng đồng quy thì (d3) phải đi qua điểm M(1;1) 
Nên : k . 1 + k – 5 = 1 => k = 3.
Kết luận k = 3
0,25
0,25
0,25
2
(2 điểm)
1. (1 điểm) 
a/ (0,5 điểm)
+ Tính được x2 = 5
+ Tính được m = -7
0,25 đ
0,25 đ
b/ (0,5 điểm)
+ , điều kiện 
+ Kết hợp với điều kiện ban đầu ta có 
0,25đ
0,25đ
2. (1 điểm)
+ Chọn ẩn và đặt đúng điều kiện cho ẩn
+ Lập được hệ phương trình
+ Giải đúng hệ được 
+ Kiểm tra điều kiện và trả lời
0,25 đ
0,25 đ
0,25 đ
0,25 đ
Bài 4
3đ
Vẽ hình cho câu a
0.5
a. Ta có tam giác AEF vuông tại A (Góc A là góc nội tiếp chắn nửa đường tròn)
Mà AB là đường cao.
=> BE.BF = AB2 (Hệ thức lượng trong tam giác vuông)
=> BE.BF = 4R2 ( Vì AB = 2R)
0.25
0.25
0.25
b. Ta có (Cùng phụ với góc BAE)
Mà ( Tam giác AOD cân)
=> 
=>Tứ giác CEFD nội tiếp đường tròn.
0.25
0.25
0.25
c. Gọi trung điểm của EF là H.
=> IH // AB (*)
 Ta lại có tam giác AHE cân tại H (AH là trung tuyến của tam giác vuông AEF, góc A = 900) => (1)
 Mà (2)
 Mặt khác ( tam giác AOC cân tại O) (3)
Từ (1), (2) và (3) => AH ^CD
Nhưng OI ^CD 
=> AH//OI (**)
Từ (*) và (**) => AHIO là hình bình hành => IH = AO = R (không đổi).
Nên I cách đường thẳng cố định EF một khoảng không đổi = R => 
I thuộc đường thẳng d // EF và cách EF một khoảng =R.
* Chú ý: Trường hợp CD ^ AB thì I thuộc AB và vẫn cách d một khoảng = R.
0.25
0.25
0.25
0.25
4
(1 điểm)
Vì xyz - => xyz(x+y+z) = 16
P = (x+y)(x+z) = x2 +xy + xz + yz = x(x+y+z) + yz
áp dụng BĐT Côsi cho hai số thực dương là x(x+y+z) và yz ta có
P = (x+y)(x+z) = x(x+y+z) + yz ; 
dấu đẳng thức xẩy ra khi 
x(x+y+z) = yz .Vậy giá trị nhỏ nhất của P là 8
0,25
0,5
0,25
PHẦN KÍ XÁC NHẬN
TÊN FILE : ĐỀ THI VÀO 10 NĂM HỌC 2015-2016 MÔN TOÁN TRƯỜNG THCS HÒA BÌNH 
TỔNG SỐ TRANG ĐỀ THI VÀ HƯỚNG DẪN CHẤM LÀ 4TRANG
NGƯỜI RA ĐỀ THI
Lưu Thị Tuyền
TỔ, NHÓM TRƯỞNG
Lã Thị Lánh
XÁC NHẬN CỦA BGH