Đề thi tuyển sinh vào lớp 10 năm học 2016 - 2017 môn thi: Toán thời gian: 120 phút (không kể thời gian giao đề)

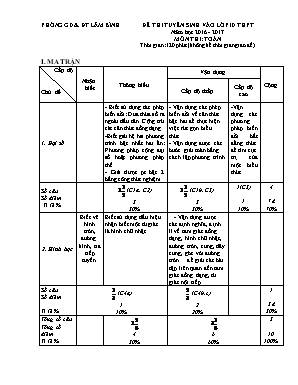
PHÒNG GD & ĐT LÂM BÌNH
ĐỀ THI TUYỂN SINH VÀO LỚP 10 THPT 
Năm học 2016 - 2017
MÔN THI: TOÁN
Thời gian: 120 phút (không kể thời gian giao đề)
I. MA TRẬN
 Cấp độ
Chủ đề 
Nhận biết
Thông hiểu
Vận dụng
Cộng
Cấp độ thấp
Cấp độ cao
1. Đại số
- Biết sử dụng các phép biến đổi: Đưa thừa số ra ngoài dấu căn. Cộng trừ các căn thức đồng dạng.
-Biết giải hệ hai phương trình bậc nhất hai ẩn: Phương pháp cộng đại số hoặc phương pháp thế.
- Giải được pt bậc 2 bằng công thức nghiệm.
- Vận dụng các phép biến đổi về căn thức bậc hai để thực hiện việc rút gọn biểu thức.
- Vận dụng được các bước giải toán bằng cách lập phương trình 
-Vận dụng các phương pháp biến đổi bất đẳng thức để tìm cực trị của một biểu thức.
Số câu 
Số điểm
 Tỉ lệ %
 (C1a, C2)
3
30%
 (C1b, C3)
3
30%
1(C5)
1
10%
4
7 đ
70%
2. Hình học
Biết vẽ hình tròn, đường kính, tia tiếp tuyến
Biết sử dụng dấu hiệu nhận biết một tứ giác là hình chữ nhật
- Vận dụng được các định nghĩa, định lí về tam giác đồng dạng, hình chữ nhật, đường tròn, cung, dây cung, góc với đường tròn ... để giải các bài tập liên quan đến tam giác đồng dạng, tứ giác nội tiếp. 
Số câu 
Số điểm 
Tỉ lệ %
 (C4a)
1
10%
 (C4b,c)
2
20%
1
3 đ
30%
Tổng số câu 
Tổng số điểm
Tỉ lệ %
4
30%
6
60%
5
10
100%
II. ĐỀ BÀI
Câu 1 (2,0 điểm): Rút gọn các biểu thức: 
	a) 
	b) 
Câu 2 (2,0 điểm)
 	a) Giải hệ phương trình: 
 	b) Giải phương trình: 
C©u 3 (2 ®iÓm): Tích của hai số tự nhiên liên tiếp lớn hơn tổng của chúng là 181. Tìm hai số đó.
Câu 4 (3 điểm): Cho đường tròn (O;R); AB và CD là hai đường kính khác nhau của đường tròn. Tiếp tuyến tại B của đường tròn (O;R) cắt các đường thẳng AC, AD thứ tự tại E và F.
 a) Chứng minh tứ giác ACBD là hình chữ nhật.
 b) Chứng minh ∆ACD ∆AFE
 c) Tứ giác CDFE nội tiếp được đường tròn.
Câu 5 (1 điểm): Tìm giá trị lớn nhất của biểu thức:
III. ĐÁP ÁN – HƯỚNG DẪN CHẤM ĐIỂM
Câu
Câu 1
Nội dung
Điểm
a) Ta cã 
0,5
0,5
b) Ta cã 
0,5
0,5
Câu 2
a) 
0,25
Vậy hệ phương trình đã cho có nghiệm duy nhất là:
 (x ; y) = (1 ; 1)
0,5
0,25
b) Ta có: > 0
0,5
Phương trình có hai nghiệm 
0,5
Câu 3
Gọi hai số tự nhiên liên tiếp là x và x + 1( Điều kiện: x )
0,5
Tích của hai số này lớn hơn tổng của chúng là 181.
 Nên ta có phương trình:
	x( x+1 ) = x + (x+1) + 181
0,5
Û x2 - x – 182 = 0
Û (-1)2 + 4.182
 = 729
Þ = 27
0,5
 ; (Loại)
Vậy hai số tự nhiên đó là: 14 và 15 
0,25
0,25
Câu 4
Vẽ hình đúng
0,5
a) Tứ giác ACBD có hai đường chéo AB và CD bằng nhau và cắt nhau tại trung điểm của mỗi đường, 
Suy ra ACBD là hình chữ nhật
0,25
0,25
b) DACD và DAFE có góc A chung (1),
Lại có (2) (góc có đỉnh ở bên ngoài đường tròn)
Mặt khác: Vì ADBC là hình chữ nhật có AC = BD và CB = AD
Nên 
Þ (3)
 Mà sđ (4) (góc nội tiếp chắn cung AD)
 Từ (2), (3) và (4) Þ (5)
Từ (1) và (5) suy ra ∆ACD ∆AFE 
0,25
0,25
0,25
0,25
0,25
0,25
c) Ta có (6) 
Từ (5) và (6) Þ 
Tứ giác CDFE có tổng hai góc đối bằng 1800 nên nội tiếp được đường tròn.
0,25
0,25
Câu 5
Ta có: 
05
Vì 
Nên MaxA = khi x = 1
0,5