Đề tham khảo kiểm tra 1 tiết chương 3 – Môn hình học 9

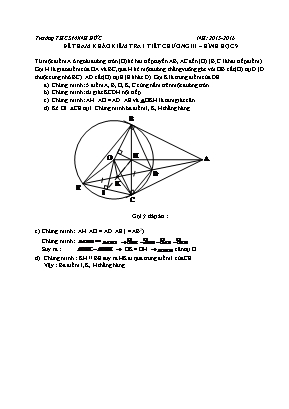
Trường THCS MINH ĐỨC	NH: 2015-2016
ĐỀ THAM KHẢO KIỂM TRA 1 TIẾT CHƯƠNG III – HÌNH HỌC 9
Từ một điểm A ở ngoài đường tròn (O) kẻ hai tiếp tuyến AB, AC đến (O) (B; C là hai tiếp điểm).
Gọi H là giao điểm của OA và BC, qua H kẻ một đường thẳng vuông góc với OB cắt (O) tại D (D thuộc cung nhỏ BC). AD cắt (O) tại E (E khác D). Gọi K là trung điểm của DE.
Chứng minh : 5 điểm A, B, O, K, C cùng nằm trên một đường tròn.
Chứng minh : tứ giác KCDH nội tiếp.
Chứng minh : AH. AO = AD. AE và OKH là tam giác cân.
Kẻ OI CE tại I. Chứng minh ba điểm I, K, H thẳng hàng.
Gợi ý đáp án :
c) Chứng minh : AH. AO = AD. AE ( = AB2)
 Chứng minh : 
 Suy ra : OK = OH cân tại O
d) Chứng minh : KH // BE suy ra HK đi qua trung điểm I của CE.
 Vậy : Ba điểm I, K, H thẳng hàng.