Đề minh họa thi vào 10 môn Toán - Trường THCS Hùng Long

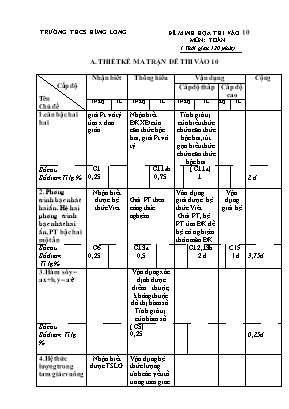
TRƯỜNG THCS HÙNG LONG
ĐỀ MINH HỌA THI VÀO 10
MÔN: TOÁN
( Thời gian 120 phút)
 A. THIẾT KẾ MA TRẬN ĐỀ THI VÀO 10
 Cấp độ
Tên 
Chủ đề 
Nhận biết
Thông hiểu
Vận dụng
Cộng
 Cấp độ thấp
Cấp độ cao
TNKQ
TL
TNKQ 
TL
TNKQ 
TL 
TNKQ 
TL 
1.căn bậc hai hai
giải Pt vô tỷ tìm x đơn giản
Nhận biết ĐKXĐ của căn thức bậc hai, giải Pt vô tỷ
Tính giá trị của biểu thức chứa căn thức bậc hai, rút gọn biểu thức chứa căn thức bậc hai
Số câu 
Số điểm Tỉ lệ %
C1
0,25
C11ab
 0,75
( C11a)
 1
2 đ 
2. Ph­¬ng tr×nh bËc nhÊt hai Èn. HÖ hai ph­¬ng tr×nh bËc nhÊt hai Èn, PT bậc hai một ẩn
Nhận biết được hệ thứcViet 
Giải PT theo công thức nghiệm
Vân dụng giải được hệ thức Viét
 Giải PT, hệ PT tìm ĐK để hệ có nghiệm thỏa mãn ĐK
Vận dụng giải hệ 
Số câu 
Số điểm 
 Tỉ lệ %
C6
0,25
C13a
0,5
C12,13b
2 đ
C15
1đ
3,75đ
3. Hàm số y= ax+b, y= ax2 
Vận dụng xác định được điểm thuộc, không thuộc đồ thị hàm số. Tính giá trị của hàm số
Số câu 
Số điểm Tỉ lệ %
( C5)
0,25
0,25đ 
4.Hệ thức lượng trong tam giác vuông
Nhận biết được TSLG
Vận dụng hệ thức lượng tính các yếu tố trong tam giac vuông
C7
0.25
C9
0,25
0,5đ 
 5.Góc và đường tròn
Vận dụng kiến thức về góc và đường tròn tính góc
Vận dụng kiến thức về góc và đường tròn trong chứng minh hình học
C 8,10
0.25
C4 a,b
2đ
C4c
1đ
3,25
Tổng số câu 
Tổng số điểm
Tỉ lệ %
Tổng số câu 
Tổng số điểm
Tỉ lệ %
3
0,75
7,5%
7
2,25
22,5%
5
7
70%
15
10
100%
ĐỀ BÀI
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (2,5 điểm)
Câu 1. Tìm x biết 
	A. 	B. 	C. 	D. 
Câu 2. Hàm số nào dưới đây đồng biến trên ?
	A. 	B. 	C. 	D. 
Câu 3. Điểm nào dưới đây thuộc đường thẳng ?
	A. 	B. 	C. 	D. 
Câu 4. Hệ phương trình có nghiệm là
	A. 	B. 	C. 	D. 
Câu 5. Giá trị của hàm số tại bằng
	A. 	B. 	C. 	D. 
Câu 6. Cho x1,x2 là hai nghiệm của phương trình x2 + 6x = 5. Khi đó x1. x2 bằng
 A. -5. B. 5. C. -6. D. 6. 
Câu 7. Cho tam giác ABC vuông tại A. Khẳng định nào dưới đây đúng?
	A.	B. 	C. 	D. 
Câu 8. Cho tứ giác ABCD nội tiếp đường tròn đường kính AC. Biết số đo bằng
A. 	B. 	
C. 	 D. 
Câu 9. Cho AABC vuông tại A, đường cao AH = 12cm, đoạn BH = 16em. Độ dài cạnh AC là
12 cm. B. 144 cm. C. 225cm. D. 15cm. 
Câu 10. Từ một điểm M bên ngoài đường tròn (0) kẻ hai tiếp tuyến MA,MB (A, B là các tiếp điểm. Kẻ đường kính BC. Cho biết góc BCA = 73°, khi đó góc AMB bằng
34°. B. 35°. C. 32°. D. 30°. 
PHẦN II. TỰ LUẬN (7,5 điểm)
Câu 11. ( 1,5 điểm): Cho biểu thức: 
a) Tìm điều kiện để A có nghĩa và rút gọn A.
b) Tìm x để A = - 1 
Câu 12 ( 1 điểm): Cho hệ phương trình 
Tìm giá trị của a để hệ có nghiệm dương
Câu 13 (1,5 điểm). Cho phương trình (m là tham số).
	a) Giải phương trình với 
	b) Gọi là hai nghiệm của phương trình. Tìm m để 
Câu 14 (2,5 điểm) 
Cho đường tròn (O; R) và dây cung CD cố định nhỏ hơn đường kính có trung điểm là H. Trên tia đối của tia DC lấy điểm S khác D. Kẻ các tiếp tuyến SA, SB với (O, R), trong đó A, B là các tiếp điểm. Đường thẳng AB cắt các đường thẳng OS, OH lần lượt tại E, F. Chứng minh rằng:
a) SEHF là tứ giác nội tiếp.
b) OH. OF = OE. OS.
c) Đường thẳng AB luôn đi qua một điểm cố định khi điểm S di động trên tia đối của tia DC.
Câu 15 (1,0 điểm). Giải hệ phương trình sau
.......................Hết..................... 
ĐÁP ÁN MÔN TOÁN
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (2,5 điểm)
Câu 1
Câu 2
Câu 3
Câu 4
Câu 5
Câu 6
Câu 7
Câu 8
Câu 9
Câu 10
D
C 
B
A
C
A
B
D
D
A
PHÀN II. TỰ LUẬN
 Câu 1: a) Tìm điều kiện để A có nghĩa. 
b)Rút gọn 
c) Tìm x để 
 Câu 2: a) Với , phương trình đã cho trở thành
Vậy phương trình có tập nghiệm 
( Hoặc giải bằng công thức nghiệm)
c) Gọi là hai nghiệm của phương trình. Tìm m để 
Theo định lí Vi-ét ta có 
Ta có 
Suy ra: 
 Câu 3: Rút y từ PT (1), thay vào (20 được (a+6)x = 8
 Nếu a = 6 hệ vô nghiệm
 Nếu a 6 thì x=
Để hệ có nghiệm dương giải hệ PT: -6 < a < 10
Câu 4
a)Vì SA, SB là tiếp tuyến của đường tròn (O) nên SA = SB và 
OA = OB (=R) nên OS là đường trung trực của AB, suy ra SOAB
Vì H là trung điểm của CD nên OHCD
Xét tứ giác SEHF có , nên H, E cùng thuộc đường tròn đường kính SF hay tứ giác SEHF nội tiếp.
b)Vì SEHF là tứ giác nội tiếp nên (cùng bù )
Suy ra 
Suy ra Suy ra OH.OF = OE.OS.
c)Tam giác AOS vuông tại A (tính chất của tiếp tuyến).
 Áp dụng hệ thức lượng ta có OE.OS = OA2 hay OE.OS = R2
Suy ra OH.OF = R2
Do O cố định, CD cố định nên H cố định
Điểm F thuộc đường thẳng OH cố định mà OF không đổi nên F cố định. 
Vậy đường thẳng AB luôn đi qua điểm F cố định khi điểm S di động trên tia đối của tia DC.
Câu 5 (1,0 điểm). Giải hệ phương trình sau
HD:
a) ĐKXĐ: x - 1; y 1
Hệ phương trình đã cho tương đương với hệ phương trình:
Đặt ; 
Hệ phương trình đã cho trở thành:
+ Với a = 1 ta có:
+ Với b = 3 ta có: 
Vậy hệ phương trình đã cho có nghiệm duy nhất (x; y) =(0; 2)
0,25
1đ
0,5đ
0,5
0,5
0,5
0,5
0,5
0,5
0,5
0,5
0,5
0,5
0,25
0,25
0,5