Đề luyện thi môn Toán học Lớp 12 (Có đáp án)

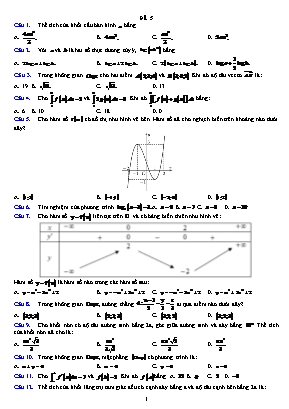
ĐỀ 5
Thể tích của khối cầu bán kính bằng
A. 	B. 	C. 	D. 
Với và là hai số thực dương tùy ý, bằng
A. 	B. 	C. 	D. 
Trong không gian cho hai điểm và . Khi đó độ dài vectơ là:
A. 19.	B. 	C. 	D. 13.
Cho và . Khi đó bằng:
A. 6.	B. 10.	C. 18.	D. 0.
Cho hàm số có đồ thị như hình vẽ bên. Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
A. 	B. 	C. 	D. 
Tìm nghiệm của phương trình A. .B. .C. .	D. .
Cho hàm số liên tục trên và có bảng biến thiên như hình vẽ:
Hàm số là hàm số nào trong các hàm số sau:
A. 	B. 	C. 	D. 
Trong không gian , đường thẳng đi qua điểm nào dưới đây?
A. 	B. 	C. 	D. 
Cho khối nón có độ dài đường sinh bằng 2a, góc giữa đường sinh và đáy bằng . Thể tích của khối nón đã cho là:
A. 	B. 	C. 	D. 
Trong không gian , mặt phẳng có phương trình là:
A. 	B. 	C. 	D. 
Cho và . Khi đó bằng A. .B. .	C. .	D. .
Thể tích của khối lăng trụ tam giác đều có cạnh đáy bằng a và độ dài cạnh bên bằng 2a là:
A. 	B. 	C. 	D. 
Tìm công thức tính thể tích của khối tròn xoay khi cho hình phẳng giới hạn bởi parabol và đường thẳng quay xung quanh trục .
A. .	B. .	C. .	D. .
Tập nghiệm S của bất phương trình là:
A. 	B. 	C. 	D. 
Cho cấp số cộng , biết và . Giá trị của bằng:
A. 4040.	B. 4400.	C. 4038.	D. 4037.
Tìm điểm biểu diễn hình học của số phức ?
A. 	B. 	C. 	D. 
Cho hàm số có đồ thị như hình vẽ:
Số điểm cực trị của hàm số đã cho là:
A. 2.	B. 3.	C. 4.	D. 5.
Họ nguyên hàm của hàm số là:
A. 	B. 
C. 	D. 
Tiếp tuyến của đồ thị hàm số tại điểm có hoành độ có phương trình là
A. .	B. .	C. .	D. .
Tìm giá trị lớn nhất của hàm số trên .
A. .	B. .	C. .	D. 
Tập nghiệm của bất phương trình là:
A. 	B. 	C. 	D. 
Cho khối chóp có đáy là hình vuông cạnh a, SA vuông góc với mặt phẳng đáy và cạnh bên SB tạo với mặt phẳng đáy góc . Thể tích của khối chóp bằng:
A. 	B. 	C. 	D. 
Biết và là 2 nghiệm của phương trình . Tính giá trị của biểu thức . A. 	B. 	C. 	D. 
Đạo hàm của hàm số là:
A. 	B. 	C. 	D. 
Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn . Tính ?
A. 0.	B. -9.	C. -10.	D. -1.
Phương trình mặt cầu có tâm và tiếp xúc với mặt phẳng là:
A. 	B. 	
C. 	D. 
Cho hàm số có đồ thị như hình vẽ:
Số nghiệm của phương trình là: A. 2.	B. 3.	C. 4.	D. 1.
Cho hình chóp S.ABC có đáy là tam giác vuông tại A có , tam giác SBC đều và mặt trong mặt phẳng vuông góc với đáy (tham khảo hình vẽ). Góc giữa SA và mặt phẳng đáy là
A. 	B. 	C. 	D. 
Cho hình lập phương với là tâm hình vuông . Biết rằng tứ diện có thể tích bằng . Tính thể tích V của khối lập phương .
A. 	B. 	C. 	D. 
Tập hợp các điểm biểu diễn số phức z thỏa mãn là:
A. Đường tròn .	B. Đường tròn .
C. Đường tròn .	D. Đường thẳng .
Cho hàm số là hàm số xác định trên , liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau:
Số tiệm cận đứng của đồ thị hàm số là:A. 1.	B. 3.	C. 4.	D. 2.
Cho hàm số liên tục trên và có đồ thị như hình vẽ, diện tích hai phần lần lượt bằng 12 và 3. Giá trị của bằng:
A. 15.	B. 9.	C. 36.	D. 27.
Trong không gian với hệ tọa độ , hai điểm . Phương trình mặt phẳng trung trực của AB là:
A. 	B. 	C. 	D. 
Đường thẳng là giao của hai mặt phẳng và thì có phương trình là:
A. 	B. C. 	D. 
Cho hàm số có đạo hàm là . Tìm số điểm cực trị của hàm số : 
 A. 6.	B. 3.	C. 1.	D. 2.
Cho hàm số liên tục trên có đồ thị như hình vẽ bên cạnh và hàm số . Khẳng định nào sau đây là khẳng định sai?
A. Hàm số đồng biến trên khoảng .	B. Hàm số đồng biến trên khoảng .
C. Hàm số nghịch biến trên khoảng .	D. Hàm số nghịch biến trên khoảng 
Trên giá sách có 4 quyển sách toán, 3 quyển sách lý, 2 quyển sách hóa. Lấy ngẫu nhiên 3 quyển sách. Tính xác suất để 3 quyển lấy ra thuộc 3 môn khác nhau.
A. 	B. 	C. 	D. 
Một khối đồ chơi gồm một khối nón xếp chồng lên một khối trụ . Khối trụ có bán kính đáy và chiều cao lần lượt là . Khối nón có bán kính đáy và chiều cao lần lượt là thỏa mãn và (tham khảo hình vẽ bên). Biết rằng thể tích của toàn bộ khối đồ chơi bằng , thể tích khối nón bằng:
A. 	B. C. 	D. 
Cho với a, b, c là các số hữu tỉ. Giá trị của bằng:
A. 	B. 	C. 	D. 
Cho hàm số với . Giá trị của là
A. 	B. 	C. 	D. 
Cho hình chóp có đáy là hình chữ nhật tâm và . Biết SC tạo với đáy một góc . Tính khoảng cách giữa hai đường thẳng AC và SB.
A. 	B. 	C. 	D. 
Cho hàm số thỏa mãn điều kiện và . Tính tích phân . A. 	B. 	C. 	D. 
Trong không gian với hệ tọa độ , phương trình nào dưới đây là phương trình hình chiếu của đường thẳng trên mặt phẳng .
A. 	B. 	C. 	D. 
Cho phương trình (với m là tham số thực). Có tất cả bao nhiêu giá trị nguyên dương của tham số m để phương trình trên có nghiệm?
A. 3.	B. 4.	C. 5.	D. Vô số.
Đồ thị hàm số cắt đường thẳng tại 4 điểm phân biệt và tạo ra các hình phẳng có diện tích thỏa mãn (như hình vẽ). Giá trị m thuộc khoảng nào sau đây?
A. 	B. 	C. 	D. 
Cho hàm số có bảng biến thiên như hình vẽ:
Số điểm cực trị của hàm số là:
A. 4.	B. 5.	C. 6.	D. 3.
Trong không gian tọa độ , cho mặt cầu , mặt phẳng và điểm . Điểm M thay đổi trên đường tròn giao tuyến của và . Giá trị lớn nhất của là:
A. 	B. 	C. 	D. 
Cho hàm số y = f(x) có đồ thị trên đoạn [-1;4] như hình vẽ bên. Số giá trị nguyên âm của tham số m để bất phương trình có nghiệm trên đoạn [-1;4] là
A. 4.	B. 5.	C. 6.	D. 7.
Xét các số phức z thỏa mãn . Đặt , giá trị lớn nhất của biểu thức là
A. 	B. 	C. 	D. 
Cho các số thực x, y thỏa mãn . Gọi M, m lần lượt là giá trị lớn nhất và nhỏ nhất của biểu thức . Khi đó bằng:
A. 	B. 	C. 	D. 
1.A
2.B
3.B
4.A
5.B
6.A
7.A
8.A
9.A
10.D
11.D
12.D
13.A
14.D
15.D
16.D
17.D
18.B
19.D
20.D
21.B
22.D
23.B
24.B
25.B
26.C
27.C
28.C
29.B
30.C
31.D
32.B
33.D
34.D
35.D
36.B
37.C
38.A
39.D
40.D
41.B
42.D
43.B
44.B
45.D
46.B
47.D
48.B
49.C
50.C
A. MA TRẬN ĐỀ 
LỚP
CHƯƠNG
CHỦ ĐỀ
MỨC ĐỘ
TỔNG
NB
TH
VD
VDC
12
CHƯƠNG 1. ỨNG DỤNG ĐẠO HÀM ĐỂ KS VÀ VẼ ĐTHS
Sự đồng biến, nghịch biến của hàm số 
1
1
11
Cực trị của hàm số 
1
1
1
GTLN, GTNN của hàm số 
1
1
Tiệm cận 
1
Nhận diện và vẽ đồ thị hàm số 
1
Tương giao
1
Tiếp tuyến 
1
CHƯƠNG 2. HÀM SỐ LŨY THỪA. HÀM SỐ MŨ. HÀM SỐ LOGARIT
Lũy thừa. Hàm số lũy thừa
1
8 
Logarit. Hàm số mũ. Hàm số logarit
1
1
PT mũ. PT loga 
1
1
1
BPT mũ. BPT loga
2
CHƯƠNG 3. NGUYÊN HÀM – TÍCH PHÂN VÀ UD
Nguyên hàm 
1
8 
Tích phân 
1
2
1
Ứng dụng tích phân 
1
1
1
CHƯƠNG 4. SỐ PHỨC
Số phức 
1
1
1
4
Phép toán trên tập số phức
Phương trình phức
1
CHƯƠNG 1. KHỐI ĐA DIỆN
Khối đa diện
3
Thể tích khối đa diện 
1
1
1
CHƯƠNG 2. KHỐI TRÒN XOAY
Khối nón 
1
3
Khối trụ
1
Khối cầu 
1
CHƯƠNG 3. PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG GIAN
Tọa độ trong không gian 
2
8
Phương trình mặt cầu 
1
1
Phương trình mặt phẳng 
1
1
Phương trình đường thẳng 
2
11
TỔ HỢP – XÁC SUẤT 
1
1
5 
CẤP SỐ CỘNG – CẤP SỐ NHÂN 
1
GÓC – KHOẢNG CÁCH 
1
1
TỔNG
21
13
11
5
50
Đề thi gồm 50 câu hỏi trắc nghiệm nội dung của đề xoay quanh chương trình Toán 12 ( chiếm 90%), ngoài ra có một số các bài toán thuộc nội dung Toán lớp 11 (Chiếm 10%). Đề thi được biên soạn dựa theo cấu trúc đề minh họa môn Toán 2021 mà Bộ Giáo dục và Đào tại đã công bố vào cuối tháng 3. Trong đó Mức độ VD - VDC (Chiếm 32%) – Đề thi ở mức độ khá . Đề thi bao gồm thêm những câu hỏi có thể ra trong đề thi chính thức. Đề thi sẽ giúp HS biết được mức độ của mình để có kế hoạch ôn tập một cách hiệu quả nhất.
B. BẢNG ĐÁP ÁN 
1.A
2.B
3.B
4.A
5.B
6.A
7.A
8.A
9.A
10.D
11.D
12.D
13.A
14.D
15.D
16.D
17.D
18.B
19.D
20.D
21.B
22.D
23.B
24.B
25.B
26.C
27.C
28.C
29.B
30.C
31.D
32.B
33.D
34.D
35.D
36.B
37.C
38.A
39.D
40.D
41.B
42.D
43.B
44.B
45.D
46.B
47.D
48.B
49.C
50.C
C. LỜI GIẢI CHI TIẾT 	
Thể tích của khối cầu bán kính bằng
A. 	B. 	C. 	D. 
Hướng dẫn giải
Đáp án A
Thể tích khối cầu bán kính là 
Với và là hai số thực dương tùy ý, bằng
A. 	B. 	C. 	D. 
Hướng dẫn giải
Đáp án B
Có 
Trong không gian cho hai điểm và . Khi đó độ dài vectơ là:
A. 19.	B. 	C. 	D. 13.
Hướng dẫn giải
Đáp án B
.
Cho và . Khi đó bằng:
A. 6.	B. 10.	C. 18.	D. 0.
Hướng dẫn giải
Đáp án A
 và .
Cho hàm số có đồ thị như hình vẽ bên. Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
A. 	B. 	C. 	D. 
Hướng dẫn giải
Đáp án B
Dựa vào đồ thị hàm số suy ra hàm số đã cho nghịch biến trên khoảng .
Tìm nghiệm của phương trình 
A. .	B. .	C. .	D. .
Hướng dẫn giải
Đáp án A
Điều kiện: .
Phương trình tương đương với
Cho hàm số liên tục trên và có bảng biến thiên như hình vẽ:
Hàm số là hàm số nào trong các hàm số sau:
A. 	B. 	C. 	D. 
Hướng dẫn giải
Đáp án A
Dựa vào bảng biến thiên ta thấy Hệ số do đó loại B và	C.
Mặt khác hàm số có 2 điểm cực trị tại nên chỉ đáp án A thỏa mãn.
Trong không gian , đường thẳng đi qua điểm nào dưới đây?
A. 	B. 	C. 	D. 
Hướng dẫn giải
Đáp án A
Thử trực tiếp.
Cho khối nón có độ dài đường sinh bằng 2a, góc giữa đường sinh và đáy bằng . Thể tích của khối nón đã cho là:
A. 	B. 	C. 	D. 
Hướng dẫn giải
Đáp án A
 (đvtt)
Trong không gian , mặt phẳng có phương trình là:
A. 	B. 	C. 	D. 
Hướng dẫn giải
Đáp án D
Cho và . Khi đó bằng
A. .	B. .	C. .	D. .
Hướng dẫn giải
Chọn D
.
Thể tích của khối lăng trụ tam giác đều có cạnh đáy bằng a và độ dài cạnh bên bằng 2a là:
A. 	B. 	C. 	D. 
Hướng dẫn giải
Đáp án D
Lăng trụ tam giác đều là lăng trụ đứng có đáy là tam giác đều.
Diện tích đáy , chiều cao .
Tìm công thức tính thể tích của khối tròn xoay khi cho hình phẳng giới hạn bởi parabol và đường thẳng quay xung quanh trục .
A. .	B. .	C. .	D. .
Hướng dẫn giải
Chọn A
Phương trình hoành độ giao điểm: .
Vậy thể tích khối tròn xoay được tính: .
Tập nghiệm S của bất phương trình là:
A. 	B. 	C. 	D. 
Hướng dẫn giải
Đáp án D
Biến đổi về .
Cho cấp số cộng , biết và . Giá trị của bằng:
A. 4040.	B. 4400.	C. 4038.	D. 4037.
Hướng dẫn giải
Đáp án D
Ta có: .
Do đó: .
Tìm điểm biểu diễn hình học của số phức ?
A. 	B. 	C. 	D. 
Hướng dẫn giải
Đáp án D
Ta có là điểm biểu diễn hình học của z.
Cho hàm số có đồ thị như hình vẽ:
Số điểm cực trị của hàm số đã cho là:
A. 2.	B. 3.	C. 4.	D. 5.
Hướng dẫn giải
Đáp án D
Dựa vào đồ thị hàm số ta chọn được đáp án	D.
Họ nguyên hàm của hàm số là:
A. 	B. C. D. 
Hướng dẫn giải
Đáp án B
.
Tiếp tuyến của đồ thị hàm số tại điểm có hoành độ có phương trình là
A. .	B. .	C. .	D. .
Hướng dẫn giải
Đáp án D
Ta có 
Với 
Hệ số góc của tiếp tuyến tại hai điểm có hoành độ là .
Phương trình tiếp tuyến tại điểm có hoành độ là .
Tìm giá trị lớn nhất của hàm số trên .
A. .	B. .	C. .	D. .
Hướng dẫn giải
Chọn D
Hàm số liên tục và xác định trên .
Ta có . Do đó .
Khi đó ; ; . Vậy .
Tập nghiệm của bất phương trình là:
A. 	B. 	C. 	D. 
Hướng dẫn giải
Đáp án B
Điều kiện: .
Vậy .
Cho khối chóp có đáy là hình vuông cạnh a, SA vuông góc với mặt phẳng đáy và cạnh bên SB tạo với mặt phẳng đáy góc . Thể tích của khối chóp bằng:
A. 	B. 	C. 	D. 
Hướng dẫn giải
Đáp án D
Diện tích hình vuông ABCD là .
Do .
Suy ra .
Thể tích khối chóp là: .
Biết và là 2 nghiệm của phương trình . Tính giá trị của biểu thức .
A. 	B. 	C. 	D. 
Hướng dẫn giải
Đáp án B
Ta có: .
Theo Viet ta có nên .
Đạo hàm của hàm số là:
A. 	B. 	C. 	D. 
Hướng dẫn giải
Đáp án B
.
Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn . Tính ?
A. 0.	B. -9.	C. -10.	D. -1.
Hướng dẫn giải
Đáp án B
.
Khi đó .
Phương trình mặt cầu có tâm và tiếp xúc với mặt phẳng là:
A. 	B. 	C. 	D. 
Hướng dẫn giải
Đáp án C
Bán kính mặt cầu bằng khoảng cách từ điểm I đến mặt phẳng .
Do đó: .
Phương trình mặt cầu là: .
Cho hàm số có đồ thị như hình vẽ:
Số nghiệm của phương trình là:
A. 2.	B. 3.	C. 4.	D. 1.
Hướng dẫn giải
Đáp án C
Phương trình 
Phương trình có 1 nghiệm và phương trình có 3 nghiệm nên phương trình đã cho có 4 nghiệm.
Cho hình chóp S.ABC có đáy là tam giác vuông tại A có , tam giác SBC đều và mặt trong mặt phẳng vuông góc với đáy (tham khảo hình vẽ). Góc giữa SA và mặt phẳng đáy là
A. 	B. 	C. 	D. 
Đáp án C
Kẻ .
Cạnh và
.
Cho hình lập phương với là tâm hình vuông . Biết rằng tứ diện có thể tích bằng . Tính thể tích V của khối lập phương .
A. 	B. 	C. 	D. 
Hướng dẫn giải
Đáp án B
Gọi x là độ dài của cạnh hình lập phương.
Ta có: .
Theo giả thiết, .
Vậy thể tích lập phương là: .
Tập hợp các điểm biểu diễn số phức z thỏa mãn là:
A. Đường tròn .	B. Đường tròn .
C. Đường tròn .	D. Đường thẳng .
Hướng dẫn giải
Đáp án C
Gọi 
 là đường tròn biểu diễn số phức z.
Cho hàm số là hàm số xác định trên , liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau:
Số tiệm cận đứng của đồ thị hàm số là:
A. 1.	B. 3.	C. 4.	D. 2.
Hướng dẫn giải
Đáp án D
Do nên đồ thị hàm số có hai đường tiệm cận đứng là .
Cho hàm số liên tục trên và có đồ thị như hình vẽ, diện tích hai phần lần lượt bằng 12 và 3. Giá trị của bằng:
A. 15.	B. 9.	C. 36.	D. 27.
Hướng dẫn giải
Đáp án B
.
Trong không gian với hệ tọa độ , hai điểm . Phương trình mặt phẳng trung trực của AB là:
A. 	B. 	C. 	D. 
Hướng dẫn giải
Đáp án D
 và là trung điểm AB.
Phương trình mặt phẳng trung trực của AB nhận vectơ và đi qua điểm I là .
Đường thẳng là giao của hai mặt phẳng và thì có phương trình là:
A. 	B. C. 	D. 
Hướng dẫn giải
Đáp án D
Ta có: .
Khi đó .
Chọn ta được .
Vậy điểm thuộc giao tuyến.
Phương trình đường thẳng giao tuyến là: .
Cho hàm số có đạo hàm là . Tìm số điểm cực trị của hàm số :
A. 6.	B. 3.	C. 1.	D. 2.
Hướng dẫn giải
Đáp án D
Hàm số có đạo hàm là .
Bảng biến thiên:
Từ BBT ta thấy hàm số có 2 điểm cực trị.
Cho hàm số liên tục trên có đồ thị như hình vẽ bên cạnh và hàm số . Khẳng định nào sau đây là khẳng định sai?
A. Hàm số đồng biến trên khoảng .	B. Hàm số đồng biến trên khoảng .
C. Hàm số nghịch biến trên khoảng .	D. Hàm số nghịch biến trên khoảng .
Hướng dẫn giải
Đáp án B
Ta có: .
Dựa vào sự tương giao của đồ thị hàm số và đường thẳng (đường thẳng này đi qua các điểm trên hình vẽ) ta có: .
Mặt khác (Do đồ thị nằm phía trên đường thẳng ) ta có bảng xét dấu:
Do đó hàm số đồng biến trên các khoảng và , nghịch biến trên các khoảng và . Khẳng định sai là	B.
Trên giá sách có 4 quyển sách toán, 3 quyển sách lý, 2 quyển sách hóa. Lấy ngẫu nhiên 3 quyển sách. Tính xác suất để 3 quyển lấy ra thuộc 3 môn khác nhau.
A. 	B. 	C. 	D. 
Hướng dẫn giải
Đáp án C
Lấy ngẫu nhiên 3 quyển sách suy ra .
Gọi A: “biến cố lấy được 3 quyển sách thuộc 3 môn khác nhau”
Ta có: .
Vậy 
Một khối đồ chơi gồm một khối nón xếp chồng lên một khối trụ . Khối trụ có bán kính đáy và chiều cao lần lượt là . Khối nón có bán kính đáy và chiều cao lần lượt là thỏa mãn và (tham khảo hình vẽ bên). Biết rằng thể tích của toàn bộ khối đồ chơi bằng , thể tích khối nón bằng:
A. 	B. 
C. 	D. 
Hướng dẫn giải
Đáp án A
Ta có: 
Cho với a, b, c là các số hữu tỉ. Giá trị của bằng:
A. 	B. 	C. 	D. 
Hướng dẫn giải
Đáp án D
Đặt .
Khi đó: .
Cho hàm số với . Giá trị của là
A. 	B. 	C. 	D. 
Hướng dẫn giải
Đáp án D
Ta có: 
Khi đó .
Cho hình chóp có đáy là hình chữ nhật tâm và . Biết SC tạo với đáy một góc . Tính khoảng cách giữa hai đường thẳng AC và SB.
A. 	B. 	C. 	D. 
Hướng dẫn giải
Đáp án B
Tam giác đều (tam giác cân có 1 góc )
Suy ra .
Ta có .
Ta có .
Trong đó:
Cho hàm số thỏa mãn điều kiện và . Tính tích phân .
A. 	B. 	C. 	D. 
Hướng dẫn giải
Đáp án D
Đặt .
Khi đó .
Suy ra .
Vậy .
Trong không gian với hệ tọa độ , phương trình nào dưới đây là phương trình hình chiếu của đường thẳng trên mặt phẳng .
A. 	B. 	C. 	D. 
Hướng dẫn giải
Đáp án B
Gọi là đường thẳng cần tìm. Gọi A là giao điểm của d và .
Gọi , cho .
Áp dụng công thức nhanh ta có: .
Do đó phương trình đường thẳng cần tìm là: .
Cho phương trình (với m là tham số thực). Có tất cả bao nhiêu giá trị nguyên dương của tham số m để phương trình trên có nghiệm?
A. 3.	B. 4.	C. 5.	D. Vô số.
Hướng dẫn giải
Đáp án B
Ta có phương trình .
Đặt .
Khi đó ta có: .
Xét hàm số với ta có .
Mặt khác .
Dựa vào BBT suy ra phương trình có nghiệm khi và chỉ khi .
Kết hợp điều kiện bài toán suy ra .
Đồ thị hàm số cắt đường thẳng tại 4 điểm phân biệt và tạo ra các hình phẳng có diện tích thỏa mãn (như hình vẽ). Giá trị m thuộc khoảng nào sau đây?
A. 	B. 	C. 	D. 
Hướng dẫn giải
Đáp án D
Giả sử đồ thị hàm số cắt đường thẳng tại 4 điểm có hoành độ thì .
Để 
Khi đó .
Cho hàm số có bảng biến thiên như hình vẽ:
Số điểm cực trị của hàm số là:
A. 4.	B. 5.	C. 6.	D. 3.
Hướng dẫn giải
Đáp án B
Ta có: .
Phương trình có 4 nghiệm.
Phương trình có nghiệm x âm nên phương trình vô nghiệm.
Do đó phương trình có 5 nghiệm.
Trong không gian tọa độ , cho mặt cầu , mặt phẳng và điểm . Điểm M thay đổi trên đường tròn giao tuyến của và . Giá trị lớn nhất của là:
A. 	B. 	C. 	D. 
Hướng dẫn giải
Đáp án D
Gọi E là hình chiếu vuông góc của A trên .
Ta có: , giao điểm của AI và là .
Mặt cầu có tâm và bán kính , bán kính đường tròn giao tuyến là . Gọi K là hình chiếu vuông góc của I trên .
Giải .
Ta có lớn nhất khi .
Mặt khác .
Cho hàm số y = f(x) có đồ thị trên đoạn [-1;4] như hình vẽ bên. Số giá trị nguyên âm của tham số m để bất phương trình có nghiệm trên đoạn [-1;4] là
A. 4.	B. 5.	C. 6.	D. 7.
Hướng dẫn giải
Đáp án B
Điều kiện để bất phương trình có nghiệm trên đoạn [-1;4] là 
Xét hàm số với 
Ta có: Đặt 
Ta thấy 
Với 
Ta có bảng biến thiên của hàm số g(x) trên đoạn [-1;4] như sau
Mặt khác 
Suy ra là giá trị cần tìm. Kết hợp 
Xét các số phức z thỏa mãn . Đặt , giá trị lớn nhất của biểu thức là
A. 	B. 	C. 	D. 
Hướng dẫn giải
Đáp án C
Ta có: 
Đặt .
Vậy w thuộc đường tròn tâm bán kính .
Cho các số thực x, y thỏa mãn . Gọi M, m lần lượt là giá trị lớn nhất và nhỏ nhất của biểu thức . Khi đó bằng:
A. 	B. 	C. 	D. 
Hướng dẫn giải
Đáp án C
Khi đó .
Phương trình bậc hai ẩn x, x tồn tại khi .
Vậy .