Đề kiểm tra lớp 11 - Môn toán đề thi học kỳ II thời gian: 90 phút (không kể thời gian thu và phát đề)

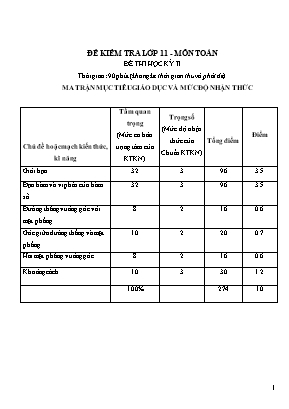
ĐỀ KIỂM TRA LỚP 11 - MÔN TOÁN
ĐỀ THI HỌC KỲ II 
Thời gian: 90 phút (không kể thời gian thu và phát đề).
MA TRẬN MỤC TIÊU GIÁO DỤC VÀ MỨC ĐỘ NHẬN THỨC
Chủ đề hoặc mạch kiến thức, kĩ năng
Tầm quan trọng
(Mức cơ bản trọng tâm của KTKN)
Trọng số
(Mức độ nhận thức của Chuẩn KTKN)
Tổng điểm
Điểm
Giới hạn
32
3
96
3.5
Đạo hàm và vi phân của hàm số
32
3
96
3.5
Đường thẳng vuông góc với mặt phẳng
8
2
16
0.6
Góc giữa đường thẳng và mặt phẳng
10
2
20
0.7
Hai mặt phẳng vuông góc
8
2
16
0.6
Khoảng cách
10
3
30
1.2
100%
274
10
MA TRẬN ĐỀ KIỂM TRA HỌC KỲ II
Chủ đề
Nhận biết
1
Thông hiểu
2
Vận dụng
3
Tổng
Giới hạn
1
1.0
1
1.0
1
1.0
3
3.0
Đạo hàm và vi phân của hàm số
2
2.0
1
 1.0
1
1.0
4
 4.0
Đường thẳng vuông góc với mặt phẳng
1
 0.5
1
0.5
Góc giữa đường thẳng và mặt phẳng
1 
 0.75
1
0.75
Hai mặt phẳng vuông góc
1
0.75
1
0.75
Khoảng cách
1
1.0
1
1.0
Tổng
4
3.5
4
3.5
3
3.0
11
10.0
BẢNG MÔ TẢ TIÊU CHÍ LỰA CHỌN CÂU HỎI, BÀI TẬP
Câu 1a. Biết tính giới hạn hữu hạn của dãy số.
Câu 1b. Vận dụng các tính chất để tính giới hạn có chứa dạng 
Câu 2. Hiểu được cách xét được tính liên tục của hàm số tại một điểm 
Câu 3a. Biết tính đạo hàm một tích.
Câu 3b. Vận dụng các công thức đạo hàm để tính đạo hàm của hàm hợp lượng giác. 
Câu 4. Biết cách viết phương trình tiếp tuyến của đồ thị hàm số tại một điểm
Câu 5. Hiểu cách giải các phương trình liên quan đến phương trình lượng giác 
Câu 6a. Biết chứng minh được đường thẳng vuông góc với mặt phẳng 
Câu 6b. Hiểu cách chứng minh được mặt phẳng vuông góc với mặt phẳng 
Câu 6c. Hiểu và tính được góc giữa đường thẳng và mặt phẳng. 
Câu 6d. Biết vận dụng các kiến thức để xác định và tính khoảng cách từ một điểm tới một mặt phẳng.
ĐỀ THI 01
MÔN TOÁN LỚP 11 - HỌC KỲ II
Năm học: 2012-2013
Thời gian: 90 phút (không kể thời gian phát đề)
Câu 1 (2.0). Tính: a) ); 	b) 
Câu 2 (1.0). Xét tính liên tục của hàm số tại điểm x0 = 1
Câu 3 (2.0). Tính đạo hàm các hàm số sau:
 a) ; b) 
Câu 4 (1.0)
Viết phương trình tiếp tuyến của parabol tại điểm A(-1;-3) .
Câu 5 (1.0) 
Cho hàm số . Hãy giải phương trình 	
Câu 6 (3.0).
 	Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA ^ (ABCD) và SA = 2a. 
a. Chứng minh .
	b. Chứng minh .
	c. Tính góc giữa SB và (SAD).
	d. Tính d(A, (SCD))
( Giám thị coi thi không giải thích gì thêm)
ĐỀ THI 02
MÔN TOÁN LỚP 11- HỌC KỲ II
Năm học: 2012-2013
Thời gian: 90 phút (không kể thời gian phát đề)
Câu 1 (2.0). Tính: a) ; 	b) 
Câu 2 (1.0). Xét tính liên tục của hàm số tại điểm x0 = -3
Câu 3 (2.0). Tính đạo hàm các hàm số sau:
 a) ; b) 
Câu 4 (1.0) 
Viết phương trình tiếp tuyến của parabol tại điểm A(2;-6).
Câu 5 (1.0) 
Cho hàm số . Hãy giải phương trình 	
Câu 6 (3.0)
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA ^ (ABCD) và SA = 2a.
	a. Chứng minh .
b. Chứng minh .
	c. Tính góc giữa SB và (SAC).
	d. Tính d(A, (SCD)).
( Giám thị coi thi không giải thích gì thêm)
ĐÁP ÁN ĐỀ 01 KIỂM TRA HỌC KÌ II – NĂM HỌC: 2012 – 2013
MÔN TOÁN LỚP 11 
CÂU
Ý
NỘI DUNG
ĐIỂM
1
a
)=lim
0,5
=- 5
0,5
b
=
0,5
0,5
2
f(1) = 6
0,25
0,50
f(x) liên tục tại xo = 1
0,25
3
a
0,25
0,25
=
0,5
b
0,75
0,25
4
Ta có nên 
0,5
Phuơng trình tiếp tuyến là : 
0,5
5
0,25
Ta có 
0,25
0,25
0,25
6
a
Vì đáy là hình vuông nên BDAC (1)
Mặt khác, vì SA(ABCD) nên SABD (2)
Từ (1) và (2) ta có (đpcm)
0.25
0,25
b
Theo (a) ta có mànên(đpcm)
0,75
c
SA ^ (ABCD) Þ SA ^ AB nên góc giữa đường thẳng SB và mặt phẳng (SAD) là góc 
Trong tam giác vuông SAB ta có: 
nên 270
Vậy góc giữa đường thẳng SB và mặt phẳng (SAD) gần bằng 270
0,25
0,5
d
Trong DSAD, vẽ đường cao AH. Ta có: AH ^ SD, AH ^ CD
 Þ AH ^ (SCD) Þ d(A,(SCD)) = AH.
Vậy 
0,5
0,25
0,25
ĐÁP ÁN ĐỀ 02 KIỂM TRA HỌC KÌ II – NĂM HỌC: 2012 – 2013
MÔN TOÁN LỚP 11 
CÂU
Ý
NỘI DUNG
ĐIỂM
1
a
=lim
0,5
=-2
0,5
b
=
0,5
0,5
2
f(-3) = -4
0,25
0,50
f(x) liên tục tại xo = -3
0,25
3
a
0,25
0,25
=
0,5
b
1
4
Ta có nên 
0,5
Phuơng trình tiếp tuyến là : 
0,5
5
0,25
Ta có 
0,25
0,25
0,25
6
a
Vì đáy là hình vuông nên CDAD (1)
Mặt khác, vì SA(ABCD) nên SACD (2)
Từ (1) và (2) ta có (đpcm)
0.25
0,25
b
Theo (a) ta có mànên
0,75
c
BO ^(SAC) Þ Góc giữa đường thẳng SB và mặt phẳng (SAC) là góc
.	
Ta có , . Trong tam giác vuông OSB ta có:
 nên 180
Góc giữa đường thẳng SB và mặt phẳng (SAC) gần bằng 180
0,25
0,5
d
Trong DSAD, vẽ đường cao AH. Ta có: AH ^ SD,
AH ^ CD Þ AH ^ (SCD) Þ d(A,(SCD)) = AH.
Vậy: 
0,5
0,25
0,25
Ban giám hiệu Tổ chuyên môn Người ra đề