Đề kiểm tra giữa kì 2 môn Toán Lớp 9

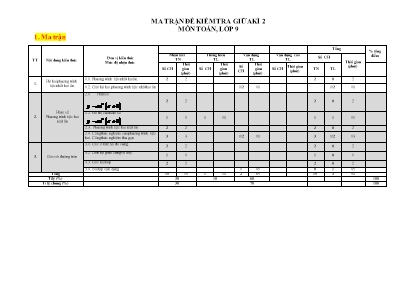
MA TRẬN ĐỀ KIỂM TRA GIỮA KÌ 2
MÔN TOÁN, LỚP 9
1. Ma trận 
TT
Nội dung kiến thức
Đơn vị kiến thức
Mức độ nhận thức
Tổng
% tổng
điểm
Nhận biết
TN
Thông hiểu 
TL
Vận dụng
TL
Vận dụng cao
TL
Số CH
Thời gian (phút)
Số CH
Thời gian (phút)
Số CH
Thời gian (phút)
Số CH
Thời gian (phút)
Số CH
Thời gian (phút)
TN
TL
Hệ hai phương trình bậc nhất hai ẩn.
1.1. Phương trình bậc nhất hai ẩn.
2
2
2
0
2
1.2. Giải hệ hai phương trình bậc nhất hai ẩn
1/2
10
1/2
10
Hàm số 
Phương trình bậc hai một ẩn
Hàm số 
2
2
2
0
2
2.2. Đồ thị của hàm số 
1
1
1
10
1
1
11
2.3. Phương trình bậc hai một ẩn
2
2
2
0
2
2.4. Công thức nghiệm của phương trình bậc hai. Công thức nghiệm thu gọn
3
3
1/2
10
3
1/2
13
Góc với đường tròn
3.1. Góc ở tâm. Số đo cung.
2
2
2
0
2
3.2. Liên hệ giữa cung và dây.
1
1
1
0
1
3.3. Góc nội tiếp
2
2
2
0
2
3.4. Bài tập vận dụng
1
45
0
1
45
Tổng
15
15
1
10
2
65
15
3
90
Tỉ lệ (%)
30
10
60
100
Tỉ lệ chung (%)
30
70
100
2. Đặc tả 
BẢNG ĐẶC TẢ KĨ THUẬT ĐỀ KIỂM TRA GIỮA KÌ 2 
MÔN TOÁN 9 
TT
Nội dung kiến thức
Đơn vị kiến thức
Mức độ kiến thức, kĩ năng cần kiểm tra, đánh giá
Số câu hỏi theo mức độ nhận thức
Nhận biết
Thông hiểu
Vận dụng 
Vận dụng cao
1
Hệ hai phương trình bậc nhất hai ẩn.
1.1. Phương trình bậc nhất hai ẩn.
Nhận biết
- Nhận biết được hpt bậc nhất hai ẩn/ chỉ ra được nghiệm của pt bậc nhất hai ẩn (Câu 1, Câu 2).
2
0
0
0
1.2. Giải hệ hai phương trình bậc nhất hai ẩn
Vận dụng
- Giải được hpt bằng pp cộng đại số hoặc pp thế (Câu 16 a).
0
0
1/2
0
2
Hàm số 
Phương trình bậc hai một ẩn
2.1. Hàm số 
Nhận biết
- Nhận biết được tính chất của hàm số (Câu 3).
- Chỉ ra được giá trị của hàm số tại giá trị cho trước của biến số (Câu 4).
2
0
0
0
2.2. Đồ thị của hàm số 
Nhận biết
- chỉ ra được điểm thuộc đồ thị hàm số/ chỉ ra được đồ thị hàm số đi qua điểm có tọa độ cho trước (Câu 5).
Thông hiểu
- Vẽ đồ thj của hàm số (Câu 17).
1
1
0
0
2.3. Phương trình bậc hai một ẩn
Nhận biết
- Chỉ ra được các hệ số của pt bậc hai cho trước/ nhận biết được pt bậc hai/ (Câu 6, 7).
2
0
0
0
2.4. Công thức nghiệm của phương trình bậc hai. Công thức nghiệm thu gọn
Nhận biết
- Nhận biết được số nghiệm của pt bậc hai/ nhận biết được nghiệm tổng quát của pt bậc hai/ nhận ra được điều kiện pt bậc hai vô nghiệm (có nghiệm kép/có hai nghiệm phân biệt) (Câu 8, 9, 10).
Vận dụng
- Giải được pt bậc hai nhờ công thức nghiệm ( công thức nghiệm thu gọn) (Câu 16 b).
3
0
1/2
0
3
Góc với đường tròn
3.1. Góc ở tâm. Số đo cung.
Nhận biết
- Nêu lên được khái niệm góc ở tâm/ số đo của cung nhỏ ( lớn)/ nhận biết được cung nhỏ hơn ( lớn hơn) (Câu 11, 12).
2
0
0
0
3.2. Liên hệ giữa cung và dây.
Nhận biết
- Chỉ ra được dây lớn hơn ( nhỏ hơn) căng cung lớn hơn ( nhỏ hơn) (Câu 13).
1
0
0
0
3.3. Góc nội tiếp
Nhận biết
- Chỉ ra được số đo của góc nội tiếp ( nhận ra hệ quả của góc nội tiếp)/ nhận biết được góc nội tiếp trên hình vẽ (Câu 14, 15).
2
0
0
0
3.4. Bài tập vận dụng
Vận dụng quan hệ giữa cung và dây, các góc với đường tròn để chứng minh hai dây bằng nhau, tam giác cân. (Câu 18a,b,c).
1
0
Tổng
15
1
2
0
4. Đề minh họa; đáp án và hướng dẫn chấm 
ĐỀ MINH HỌA
ĐỀ KIỂM TRA GIỮA KÌ 2 
Môn TOÁN, Lớp 9
 Thời gian làm bài: 90 phút, không tính thời gian phát đề
I. PHẦN TRẮC NGHIỆM
Phương trình nào sau đây là phương trình bậc nhất hai ẩn?
A. .	B. 	
C. 	D. 
Phương trình nhận cặp số nào sau đây là nghiệm?
	B. 	C. 	D. 
Cho hàm số . Kết luận nào sau đây đúng?
Hàm số nghịch biến khi 	
Hàm số nghịch biến khi 	
Hàm số nghịch biến khi 	
Hàm số nghịch biến khi 
Giá trị của hàm số tại là
28	B. 12	C. 21	D. - 28
Đồ thị hàm số đi qua điểm nào sau đây?
A. 	B. 	C. 	D. 
Hệ số của phương trình là
9	B. - 9	C. 0	D. 18
Trong các phương trình sau, phương trình nào là phương trình bậc hai một ẩn
	B. 	
C. 	 D. 
Cho phuơng trình có biệt thức , khi đó, phương trình đã cho
Vô nghiệm	B. có nghiệm kép	
C. có hai nghiệm phân biệt	D. có 1 nghiệm
Cho phuơng trình có biệt thức , khi đó, phương trình có hai nghiệm là
A. 	B. 	
C. 	D. 
Cho phuơng trình có biệt thức . Phương trình đã cho có hai nghiệm phân biệt khi
	B. 	C. 	D. 
Chọn khẳng định đúng. Góc ở tâm là góc
có đỉnh nằm trên đường tròn
B. có đỉnh trùng với tâm đường tròn
C. có hai cạnh là hai đường kính của đường tròn	
D. có đỉnh nằm trên bán kính của đường tròn
Chọn khẳng định đúng. Trong một đường tròn, số đo cung nhỏ bằng
Số đo cung lớn	 B. số đo góc ở tâm chắn cung đó	
C. Số đo góc ở tâm chắn cung lớn D. số đo của cung chắn nửa đường tròn
Chọn khẳng định đúng. Cho đường tròn có dây cung , khi đó
cunglớn hơn cung B. cungnhỏ hơn cung 
C. cungbằng cung D. số đo cungbằng hai lần số đo cung 
Góc nội tiếp có số đo nhỏ hơn hoặc bằng 900 có số đo
bằng nửa số đo góc ở tâm cùng chắn một cung	
B. bằng số đo góc ở tâm cùng chắn một cung	
C. bằng số đo cung bị chắn	
D. bằng nửa số đo cung lớn
Khẳng định nào sau đây sai?
Trong một đường tròn, góc nội tiếp chắn nửa đường tròn là góc vuông	
B. Trong một đường tròn, hai góc nội tiếp bằng nhau chắn hai cung bằng nhau
C. Trong một đường tròn, hai góc nội tiếp cùng chắn một cung thì bằng nhau
D. Trong một đường tròn, hai góc nội tiếp bằng nhau thì cùng chắn một cung
II. PHẦN TỰ LUẬN
Câu 16 (3,0 điểm). 
Giải hệ phương trình 
Giải phương trình 
Câu 17 (1,0 điểm).
 Vẽ đồ thị của hàm số .
Câu 18 (3,0 điểm). 
Các đường cao hạ từ A và B của tam giác ABC cắt nhau tại H (góc C khác 900) và cắt đường tròn ngoại tiếp tam giác ABC lần lượt tại D và E. Chứng minh rằng:
cân
-----------HẾT----------
ĐÁP ÁN VÀ HƯỚNG DẪN CHẤM ĐỀ KIỂM TRA GIỮA KÌ 2
Môn TOÁN, Lớp 9
I. PHẦN TRẮC NGHIỆM
Câu
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Đáp án
C
C
C
D
B
C
C
C
C
A
B
B
A
A
D
* Mỗi câu trắc nghiệm đúng được 0,20 điểm.
II. PHẦN TỰ LUẬN
Câu hỏi
Nội dung
Điểm
Câu 16
(3,0 điểm)
a) 
Vậy nghiệm của hệ phương trình là 
0,5
0,25
0,25
0,25
0,25
b) 
phương trình có hai nghiệm phân biệt:
0,25
0,5
0,25
0,25
0,25
Câu 17
(1,0 điểm)
Lập bảng giá trị:
-2
-1
0
1
2
4
1
0
1
4
Đồ thị:
0,5
0.5
Câu 18
(3,0 điểm)
Vẽ hình đúng đến ý a 
0,5
a) Ta có (cùng phụ với )
Mà và là hai góc nội tiếp chắn và 
 (đpcm)
0,25
0,25
0,5
b) Theo chứng minh a ta có: 
 (hai góc nội tiếp chắn hai cung bằng nhau)
Mà 
cân tại B
0,25
0,25
0,25
0,25
c) Theo chứng minh b ta có IH = ID 
mà tại I
 cân tại C (đpcm)
0,25
0,25
10,0
-----------HẾT----------