Đề kiểm tra cuối học kỳ II môn Toán 9 - Năm học 2021-2022

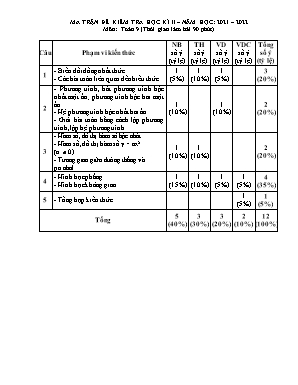
MA TRẬN ĐỀ KIỂM TRA HỌC KÌ II – NĂM HỌC: 2021 – 2022
Môn: Toán 9 (Thời gian làm bài 90 phút)
Câu
Phạm vi kiến thức
NB
số ý 
(tỷ lệ)
TH
số ý 
(tỷ lệ)
VD
số ý 
(tỷ lệ)
VDC
số ý 
(tỷ lệ)
Tổng
số ý 
(tỷ lệ)
1
- Biến đổi đồng nhất thức
- Các bài toán liên quan đến biểu thức
1
(5%)
1
(10%)
1
(5%)
3
(20%)
2
- Phương trình, bất phương trình bậc nhất một ẩn; phương trình bậc hai một ẩn.
- Hệ phương trình bậc nhất hai ẩn.
- Giải bài toán bằng cách lập phương trình, lập hệ phương trình.
1
(10%)
1
(10%)
2
(20%)
3
- Hàm số, đồ thị hàm số bậc nhất. 
- Hàm số, đồ thị hàm số y = ax2 
(a 0)
- Tương giao giữa đường thẳng và parabol.
1
(10%)
1
(10%)
2
(20%)
4
- Hình học phẳng
- Hình học không gian
1
(15%)
1
(10%)
1
(5%)
1
(5%)
4
(35%)
5
- Tổng hợp kiến thức
1
(5%)
1
(5%)
Tổng
5
(40%)
3
(30%)
3
(20%)
2
(10%)
12
(100%)
PHÒNG GD & ĐT ĐÔNG HƯNG
Trường TH & THCS HOA LƯ
ĐỀ KIỂM TRA CUỐI HỌC KỲ II
NĂM HỌC 2021-2022
Môn: Toán 9
( Thời gian làm bài: 90 phút )
Bài 1 (2 điểm):
Cho hai biểu thức và (với )
a) Tính giá trị của biểu thức A khi 
b) Rút gọn biểu thức B
c) Cho Tìm x để P < 3.
Bài 2 (2 điểm ) Cho hệ phương trình: (m là tham số).
a.Tìm m để hệ phương trình có nghiệm (x ; y) trong đó x = 2.
b.Tìm m để hệ phương trình có nghiệm duy nhất (x ; y) thoả mãn 2x + y = 9.
 Bài 3 (2,5 điểm): Trong mặt phẳng tọa độ xOy cho đường thẳng (d) có phương trình:
y = 2mx + 5 và parabol (P): y = x2. 
a. Tìm m để đường thẳng (d) đi qua điểm A(1; 3).
b. Chứng tỏ rằng đường thẳng (d) luôn cắt (P) tại hai điểm phân biệt với mọi m.
c. Gọi lần lượt là hoành độ giao điểm của (d) và (P). Tìm m sao cho: .
Bài 4 (3 điểm): Cho đường tròn (O) đường kính AB = 2R. Lấy điểm I thuộc đoạn thẳng AB sao cho IA < IB, kẻ dây MN vuông góc với đường kính AB tại I. Trên đoạn MI lấy điểm E ( E khác M, I). Tia AE cắt đường tròn tại điểm thứ hai là K.
a. Chứng minh tứ giác IEKB nội tiếp.
b. Chứng minh: AE.AK + BI.BA = 4R2
c. Xác định vị trí của điểm I sao cho chu vi tam giác MIO đạt giá trị lớn nhất?
Bài 5 (0.5 điểm): Giải phương trình: 
............................Hết..........................
HƯỚNG DẪN CHẤM VÀ BIỂU ĐIỂM
Câu
Ý
Nội dung cần đạt
Điểm
1
a
* Khi thì thì 
* Vậy khi thì 
0.5
2.5
b
0.25
0.25
0.25
0.25
c
Ta có: 
Kết hợp điều kiện xác định duy ra thì 
0.25
0.25
0.25
0.25
2
a
Với x = 2 thì từ phương trình x – y = -6 Þ y = 8.
Thay x = 2, y = 8 vào phương trình thứ nhất, ta được: 2m + 16 = 18 Þ m = 1.
Vậy giá trị cần tìm m = 1.
0.25
0.25
0.25
0.25
2
b
Điều kiện để hệ phương trình đã cho có nghiệm duy nhất: .
Nghiệm duy nhất (x ; y) của hệ đã cho thoả mãn điều kiện đề bài là nghiệm của hệ: 
Từ đó, ta có: 5m – 2 = 18 Û m = 4 (thoả mãn m ¹ -2).
Vậy giá trị cần tìm là m = 4.
0.25
0.25
0.25
0.25
3
a
HS biết thay x = 1, y =3 vào phương trình đường thẳng (d)
Tính đúng: 2.m.1+ 5 = 3 nên m = - 1
0.25
0.5
2.5
b
HS biết xét phương trình hoành độ giao điểm:
 x2 = 2mx + 5 
HS tính đúng: 
và kết luận 
Kết luận được đường thẳng (d) luôn cắt (P) tại hai điểm phân biệt với mọi m.
0.25
0.25
0.25
0.25
c
HS chỉ ra đúng hệ thức Viet: 
0.25
0.5
4
HS vẽ hình đúng 
0.5
a
HS chứng minh được (góc nội tiếp chắn nửa đường tròn)
Chứng minh được: Tứ giác IEKB nội tiếp 
0.5
0.5
3
b
HS chứng minh được (hai góc nội tiếp chắn hai cung bằng nhau AM, BM)
HS chứng minh được (; )
0.25
HS chỉ ra từ câu b có: 
 suy ra: AE.AK = AM2 (1)
HS áp dụng hệ thức cạnh và đường cao trong tam giác vuông AMB chứng minh được: BI.BA = BM2 (2)
Cộng vế theo vế của (1) và (2) suy ra: 
AE.AK + BI.BA = AM2 + BM2 = AB2 = 4R2
0.25
0.25
0.25
d
HS chỉ ra được chu vi tam giác MIO lớn nhất khi và chỉ khi MI + MO lớn nhất. 
Áp dụng bất đẳng thức Bunhiacopski ta có: 
(MI + IO)2 2(MI2 + IO2) = 2R2
Dấu “=” xảy ra khi và chỉ khi IO = MI = 
0.25
0.25
5
ĐK hoặc 
Đặt 
+ Với a = b (t/m)
+ Với a + b = 1 , HS chứng minh phương trình vô nghiệm.
Vậy phương trình chỉ có một nghiệm là: 
0.25
0.25