Đề kiểm tra 1 tiết chương 3 hình học môn: Toán- Khối 11 thời gian: 45 phút

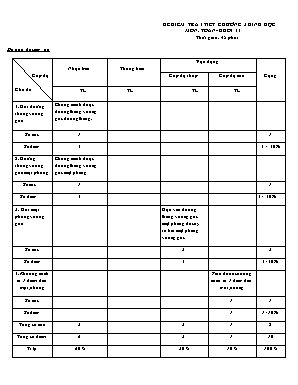
 ĐỀ KIỂM TRA 1 TIẾT CHƯƠNG 3 HÌNH HỌC MÔN: TOÁN- KHỐI 11
 Thời gian: 45 phút
Ma trận đề kiểm tra
 Cấp độ
Chủ đề
Nhận biết
Thông hiểu
Vận dụng
Cộng
Cấp độ thấp
Cấp độ cao
TL
TL
TL
TL
1. Hai đường thẳng vuông góc
Chứng minh được đường thẳng vuông góc đường thẳng.
Số câu
1
1
Số điểm
3
3 = 30%
2. Đường thẳng vuông góc mặt phẳng
Chứng minh được đường thẳng vuông góc mặt phẳng
 Số câu
1
1
 Số điểm
3
3= 30%
3. Hai mặt phẳng vuông góc
Dựa vào đường thẳng vuông góc mặt phẳng để suy ra hai mặt phẳng vuông góc
Số câu
2
2
 Số điểm
3
3=30%
4. Khoảng cách từ 1 điểm đến mặt phẳng
Tính được khoảng cách từ 1 điểm đến mặt phẳng
Số câu
1
1
Số điểm
1
1=10%
Tổng số câu
2
2
1
5
Tổng số điểm
6
3
1
10
Tỉ lệ
60%
30%
10%
100%
ĐỀ BÀI
Bài 1 ( 6 điểm) Cho hình chóp SABC có SA vuông góc (ABC). Đáy ABC là tam giác vuông tại B, kẻ đường cao AD, AE của tam giác SAB, tam giác SAC.
Chứng minh tam giác SBC vuông tại B
Chứng minh AD vuông góc mặt phẳng SBC, từ đó suy ra tam giác ADE vuông.
Bài 2: ( 3 điểm) Cho hình chóp SABCD có ABCD là hình vuông cạnh a. Hình chiếu của S trên (ABCD) trùng với trung điểm I của AB. Góc giữa SA và (ABCD) bằng 600.
Chứng minh: CM vuông góc (SID), từ đó suy ra (SCM) vuông góc (SID).
Tính khoảng cách từ điểm A đến (SCD)
Bài
Nội dung
Điểm TP
1
(6 đ)
- Vẽ hình đúng + nét khuất 
a) - Ta có BC ^ AB ( gt )
 - BC ^ SA ( SA ^ ( ABCD) )
Þ BC ^ (SAB) nên BC ^ SB
 - Do đó tam giác SBC vuông tại B
b) Vì BC ^ (SAB) nên BC ^ AD
 mà SB ^ AD (gt)
Þ AD ^ (SBC) nên AD ^ DE 
Vậy tam giác ADE vuông tại D
0.5đ
 1đ
 1.5đ
 1 đ
 1 đ
 1 đ
Bài 2
Vẽ đúng hình cho cả 2 câu
Hai tam giác vuông DAI và tam giác CDM bằng nhau nên góc DCM bằng góc IDA mà tổng số đo góc DCM và DCM bằng 900 nên tổng số đo góc IDA và CMD bằng 900 
Do đó CM ^ DI
Ta lại có: CM ^ SI
Nên CM ^ (SDI)
Hay (SCM) ^ (SDI)
Gọi N là trung điểm CD
Trong tam giác SIN, kẻ IH ^ SN
Chứng minh được CD ^ (SIN) Þ CD ^ IH
Nên IH ^ (SCD) Do đó d( A, (SCD)) = d(I, (SCD)) = IH 
Xét tam giác SIA có 
Xét tam gi1c SIN vuông có đường cao IH
0.5đ
1 đ
0.5đ
0.5đ
 0.5đ
 0.25đ
 0.25đ
 0.25đ
0.25đ