Đề khảo sát thi vào lớp 10 THPT môn Toán - Năm học 2020-2021 (Có đáp án)

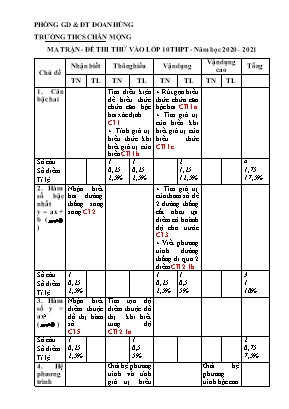
PHÒNG GD & ĐT ĐOAN HÙNG
TRƯỜNG THCS CHÂN MỘNG
MA TRẬN - ĐỀ THI THỬ VÀO LỚP 10 THPT - Năm học 2020 – 2021
Chủ đề
Nhận biết
Thông hiểu
Vận dụng
Vận dụng cao
Tổng
TN
TL
TN
TL
TN
TL
TN
TL
1. Căn bậc hai
Tìm điều kiện để biểu thức chứa căn bậc hai xác định
CI.1
+ Tính giá trị biểu thức khi biết giá trị của biến CII.1b
+ Rút gọn biểu thức chứa căn bậc hai CII.1a
+ Tìm giá trị của biến khi biết giá trị của biểu thức CII.1c
Số câu 
Số điểm
Tỉ lệ
1
0,25
2,5%
1
0,25
2,5%
2
1,25
12,5%
4
1,75
17,5%
2. Hàm số bậc nhất
y = ax + b ( )
Nhận biết hai đường thẳng song song CI.2
+ Tìm giá trị của tham số để 2 đường thẳng cắt nhau tại điểm có hoành độ cho trước CI.3
+ Viết phương trình đường thẳng đi qua 2 điểm CII.2.1b
Số câu 
Số điểm
Tỉ lệ
1
0,25
2,5%
1
0,25
2,5%
1
0,5
5%
3
1
10%
3. Hàm số y = ax2 
( )
Nhận biết điểm thuộc đồ thị hàm số
CI.5
Tìm tọa độ điểm thuộc đồ thị khi biết tung độ CII.2.1a
Số câu 
Số điểm
Tỉ lệ
1
0,25
2,5%
1
0,5
5%
2
0,75
7,5%
4. Hệ phương trình
Giải hệ phương trình và tính giá trị biểu thức giữa hai nghiệm CI.4
Giải hệ phương trình bậc cao CII.4
Số câu 
Số điểm
Tỉ lệ
1
0,25
2,5%
1
1
10%
2
1,25
12,5%
5. Phương trình bậc hai và ứng dụng của hệ thức Vi ét
+ Giá trị biểu thức đối xứng giữa hai nghiệm của pt CI.6
+ Tìm giá trị của tham số để phương trình bậc hai nhận x = x0 là nghiệm CI.7
Tính giá trị của biểu thức đối xứng giữa hai nghiệm của pt CII.2.2
Số câu 
Số điểm
Tỉ lệ
2
0,5
5%
1
1
10%
3
1,5
15%
6. Hệ thức lượng trong tam giác vuông
Tỉ số lượng giác của góc nhọn CI.8
+ Tính độ dài cạnh trong tam giác vuông CI.9
Số câu 
Số điểm
Tỉ lệ
1
0,25
2,5%
1
0,25
2,5%
2
0,5
5%
7. Góc với đường tròn
+ Tính số đo góc
CI.10
+ Chứng minh 1 đường thẳng là tiếp tuyến CII.3c
Số câu 
Số điểm
Tỉ lệ
1
0,25
2,5%
1
1
10%
2
1,2 5
12,5%
8. Tứ giác nội tiếp
Chứng minh tứ giác nội tiếp, chỉ rõ tâm CII.3a
Chứng minh đặc tính hình học CII.3b
Số câu 
Số điểm
Tỉ lệ
1
1
10%
1
1
10%
2
2
20%
Tổng câu 
Tổng điểm
Tỉ lệ
3
0,75
7,5%
5
1,25
12,5%
3
1,75
17,5%
2
0,5
5%
5
3,75
37,5%
2
2
20%
20
10
100%
PHÒNG GD & ĐT ĐOAN HÙNG
TRƯỜNG THCS CHÂN MỘNG
ĐỀ KHẢO SÁT THI VÀO LỚP 10 THPT NĂM HỌC 2020 – 2021
MÔN TOÁN
Thời gian làm bài: 120 phút
PHẦN 1. TRẮC NGHIỆM KHÁCH QUAN (2,5 điểm)
Câu 1. Với giá trị nào của x thì biểu thức xác định ?
A. .	B. .	C. .	D. 
Câu 2. Cho đường thẳng . Đường thẳng song song với đường thẳng là:
	A. 	B. 	C. 	D. 
Câu 3. Với giá trị nào của để đồ thị hàm số cắt trục hoành tại điểm có hoành độ bằng ?
A. .	B. .	C. .	D. .
Câu 4. Hệ phương trình có nghiệm . Khi đó giá trị biểu thức bằng
	A. 	B. 	C. 11	D. 
Câu 5. Đồ thị hàm số không đi qua điểm nào trong các điểm sau đây ?
(-2 ; 2) B.(2 ;2) C. ( ; ) D.( ;1)
Câu 6. Gọi là hai nghiệm của phương trình Tính 
A. 	B. 	C. 	D. 
Câu 7. Tìm tất cả các giá trị của tham số để phương trình có hai nghiệm phân biệt.	
A. 	B. 	C. 	D. 
Câu 8. Cho tam giác vuông tại , hệ thức nào sau đây sai?
 A. B. 
 C. 	 D. 	 
Câu 9. Cho tam giác ABC vuông tại A có đường cao AH có BH = 6 cm; CH = 12 cm. Độ dài cạnh góc vuông AB là:
A.6cm     B.6 cm     C.6 cm      D.12 cm
Câu 10. Trong hình vẽ bên, giả sử và Tính số đo của góc 
 A. C. 
B. D. 
PHẦN 2. TỰ LUẬN (7,5 điểm)
Câu 1 (1,5 điểm).
Cho biểu thức ()
a) Tính giá trị của biểu thức A khi 
b) Rút gọn 
c) Tìm các giá trị của x để có giá trị bằng 2. 
Câu 2 (2,0 điểm).
1. Cho hàm số . 
a) Biết các điểm A, B thuộc đồ thị hàm số và có tung độ bằng . Tìm tọa độ các điểm A, B.
b) Viết phương trình đường thẳng đi qua hai điểm và .
2. Cho phương trình (tham số m).
 Tìm m để phương trình có nghiệm thỏa mãn 
Câu 3 (3 điểm).
Cho đường tròn có đường kính cố định, đường thẳng là tiếp tuyến của đường tròn tại . Từ một điểm ( khác A và B) bất kỳ thuộc đường tròn, kẻ đường kính . Gọi lần lượt là giao điểm của đường thẳng với đường thẳng 
a) Chứng minh tam giác là tam giác vuông và .
b) Chứng minh tứ giác là một tứ giác nội tiếp.
c) Gọi là trực tâm của tam giác Chứng minh rằng khi thay đổi trên đường tròn thì thuộc một đường tròn cố định.
Câu 4 (1,0 điểm).
	Cho các số thỏa mãn Tìm giá trị nhỏ nhất và giá trị lớn nhất của biểu thức 
HƯỚNG DẪN CHẤM ĐỀ KHẢO SÁT THI VÀO LỚP 10 MÔN TOÁN
NĂM HỌC 2020 – 2021
PHẦN 1. TRẮC NGHỆM (2,5 điểm) Mỗi câu đúng 0,25 điểm
Câu
1
2
3
4
5
6
7
8
9
10
Đáp án
B
D
D
B
C
A
A
A
B
B
PHẦN 2. TỰ LUẬN (7,5 điểm)
Câu
Đáp án
Điểm
Câu 1
(1,5 điểm)
Cho biểu thức 
a) Tính giá trị của biểu thức A khi 
b) Rút gọn Q;
c) Tìm các giá trị của x để Q có giá trị bằng 2
Với (thỏa mãn điều kiện) tính được A= 
ĐKXĐ: 
0,5
b) 
0,25
0,25
c) 	
.(Thỏa mãn ĐKXĐ)
0,25
0,25
Câu 2
(2 điểm)
1. Cho hàm số . 
a) Biết các điểm A, B thuộc đồ thị hàm số và có tung độ bằng -8. Tìm tọa độ các điểm A, B.
b) Viết phương trình đường thẳng đi qua hai điểm và .
a) Các điểm A, B thuộc đồ thị hàm số và có tung độ bằng - 8 nên 
 và 
0,25
0,25
b) Giả sử phương trình đường thẳng đi qua 2 điểm A và B có dạng: . Khi đó:
Vậy phương trình đường thẳng đi qua 2 điểm A và B là: 
0,25
0,25
2. Vì phương trình có nghiệm nên ta có: 
0,25
Lại có(3)
Ta có hệ phương trình 
Thay vào (1) ta được
0,25
0,25
0,25
Câu 3 (3,0 điểm)
Cho đường tròn có đường kính cố định, đường thẳng là tiếp tuyến của đường tròn tại . Từ một điểm ( khác A và B) bất kỳ thuộc đường tròn, kẻ đường kính . Gọi lần lượt là giao điểm của đường thẳng với đường thẳng 
a) Chứng minh tam giác là tam giác vuông và .
b) Chứng minh tứ giác là một tứ giác nội tiếp.
c) Gọi là trực tâm của tam giác Chứng minh rằng khi thay đổi trên đường tròn thì thuộc một đường tròn cố định.
ĐÁP ÁN
ĐIỂM
a)(1,0đ) 
Vì MN là đường kính của đường tròn (O) nên suy ra tam giác NAM là tam giác vuông tại A
0,50 đ
DAC vuông tại A(cmt) đường cao AB (gt) suy ra 
0,50 đ
b) (1,5đ)
DAC vuông tại A(cmt) đường cao AB (gt) suy ra (cùng phụ với góc C) mà (do OA=OB) 
0,75 đ
Vì nên tứ giác CDNM nội tiếp được một đường tròn.
0,75 đ
c) (0,50) Vì H là trực tâm củaMCD suy ra 
Từ D, A, H thẳng hàng mà AD//BM (Cùng AC) suy ra AH//BM lại có AB//HM (Cùng DC) tứ giác ABMH là hình bình hành, suy ra AB//HM và AB=HM.
0,25 đ
Lấy P đối xứng với B qua A (vì A, B có định nên P cố định) 
 AP//HM và AP=HM tứ giác PAMH là hình bình hành 
 PH//AM mà 
H thuộc đường tròn đường kính AP cố định.
0,25 đ
Câu 5 (1,0 điểm) Cho các số x, y thỏa mãn. Tìm giá trị nhỏ nhất và giá trị lớn nhất của biểu thức 
ĐÁP ÁN
ĐIỂM
*) Tìm GTLN (0,50đ)
Có: 
0,25 đ
Dấu “=” xảy ra khi.
Vậy GTLN của là 32 khi 
0,25 đ
*) Tìm GTNN (0,50đ)
0,25 đ
Dấu “=” xảy ra khi.
Vậy GTNN của là khi 
0,25 đ
------- HẾT -------