Đề 9 thi thử kỳ thi thpt quốc gia môn : Toán thời gian làm bài 180 phút

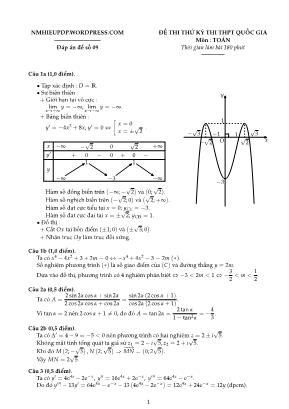
NMHIEUPDP.WORDPRESS.COM ĐỀ THI THỬ KỲ THI THPT QUỐC GIA
———————— Mụn : TOÁN
Đỏp ỏn đề số 09 Thời gian làm bài 180 phỳt
————
Cõu 1a (1,0 điểm).
• Tập xỏc định : D = R.
• Sự biến thiờn :
+ Giới hạn tại vụ cực :
lim
x→+∞ y = −∞; limx→−∞ y = −∞.
+ Bảng biến thiờn :
y′ = −4x3 + 8x; y′ = 0⇔
[
x = 0
x = ±√2 .
x −∞ −√2 0 √2 +∞
y′ + 0 − 0 + 0 −
y
−∞
1
−3
1
−∞
Hàm số đồng biến trờn
Ä−∞;−√2ọ và Ä0;√2ọ.
Hàm số nghịch biến trờn
Ä−√2; 0ọ và Ä√2;+∞ọ.
Hàm số đạt cực tiểu tại x = 0; yCT = −3.
Hàm số đạt cực đại tại x = ±√2; yCĐ = 1.
• Đồ thị :
+ Cắt Ox tại bốn điểm (±1; 0) và ı√3; 0ọ.
+ Nhận trục Oy làm trục đối xứng.
y
xO
−3
1
−1 1
−√2 √2
−√3 √3
Cõu 1b (1,0 điểm).
Ta cú x4 − 4x2 + 3+ 2m = 0⇔ −x4 + 4x2 − 3 = 2m (∗).
Số nghiệm phương trỡnh (∗) là số giao điểm của (C) và đường thẳng y = 2m.
Dựa vào đồ thị, phương trỡnh cú 4 nghiệm phõn biệt⇔ −3 < 2m < 1⇔ −3
2
< m <
1
2
.
Cõu 2a (0,5 điểm).
Ta cú A =
2 sin 2α cos α+ sin 2α
2 cos 2α cos α+ cos 2α
=
sin 2α (2 cos α+ 1)
cos 2α (2 cos α+ 1)
.
Vỡ tan α = 2 nờn 2 cos α+ 1 6= 0, do đú A = tan 2α = 2 tan α
1− tan2α = −
4
3
.
Cõu 2b (0,5 điểm).
Ta cú ∆′ = 4− 9 = −5 < 0 nờn phương trỡnh cú hai nghiệm z = 2± i√5.
Khụng mất tớnh tổng quỏt ta giả sử z1 = 2− i
√
5, z2 = 2+ i
√
5.
Khi đú M
Ä
2;−√5ọ ,N Ä2;√5ọ⇒ −−→MN = Ä0; 2√5ọ.
Vậy MN = 2
√
5.
Cõu 3 (0,5 điểm).
Ta cú y′ = 4e4x − 2e−x, y′′ = 16e4x + 2e−x, y′′′ = 64e4x − e−x.
Do đú y′′′ − 13y′ = 64e4x − e−x − 13 Ä4e4x − 2e−xọ = 12e4x + 24e−x = 12y (đpcm).
1
Cõu 4 (1,0 điểm).
Nhận thấy y = 0 khụng thỏa món hệ.
Với y 6= 0, ta cú hệ tương đương

27x3 + 7 =
8
y3
(1)
9
x2
y
+ 1 = 6
x
y2
(2)
.
Từ (2) ta cú 1 = −9x
2
y
+ 6
x
y2
thay vào (1) được :
27x3 − 63x
2
y
+ 42
x
y2
− 8
y3
= 0⇔ 27(xy)3 − 63(xy)2 + 42xy− 8 = 0⇔

xy =
1
3
xy =
2
3
xy =
4
3
Với xy =
1
3
⇒ x = 1
3y
thay vào (2) được
1
y3
+ 1 =
2
y3
⇔ y = 1⇒ x = 1
3
.
Với xy =
2
3
⇒ x = 2
3y
thay vào (2) được
4
y3
+ 1 =
4
y3
⇔ 1 = 0 (vụ lý).
Với xy =
4
3
⇒ x = 4
3y
thay vào (2) được
16
y3
+ 1 =
8
y3
⇔ y = −2⇒ x = −2
3
.
Vậy hệ cú hai nghiệm (x; y) =
ầ
1
3
; 1
ồ
và (x; y) =
ầ
−2
3
;−2
ồ
.
Cõu 5 (1,0 điểm).
Đặt t = sin x ⇒ dt = cos xdx.
Đổi cận x =
pi
6
⇒ t = 1
2
; x =
pi
2
⇒ t = 1, ta cú I =
1∫
1
2
ln(1+ t)
t2
dt.
Đặt
 u = ln(1+ t)dv = 1
t2
dt
⇒

du =
1
1+ t
dt
v = −1
t
, ta cú :
I = − ln(1+ t)
t
∣∣∣∣∣
1
1
2
+
1∫
1
2
1
t(1+ t)
dt = − ln 2+ 2 ln 3
2
+
1∫
1
2
ầ
1
t
− 1
1+ t
ồ
dt
= 2 ln 3− 3 ln 2+ (ln |t| − ln |1+ t|)|11
2
= 3 ln 3− 4 ln 2 = ln 27
16
Vậy I = ln
27
16
.
Cõu 6 (1,0 điểm).
Ta cú SA⊥(ABC)⇒ AB là hỡnh chiếu của SB trờn (ABC).
Do đú gúc giữa SB và (ABC) là ’SBA⇒’SBA = 300.
Gọi I là trung điểm BC, ta cú
AI⊥BCSI⊥BC ⇒ (SIA)⊥BC
Suy ra (SIA) là mặt phẳng trung trực của BC.
Khi đú BI⊥(SIA) nờn SI là hỡnh chiếu của SB trờn (SIA).
Do đú gúc giữa SB và (SIA) là ‘ISB⇒ ‘ISB = 450.
Suy ra ∆SBC vuụng cõn tại S nờn BC = 2SI = 2a; SB =
BC√
2
= a
√
2.
2
AB
C
S
I
Trong ∆SAB cú SA = SB sin 300 =
a
√
2
2
⇒ AI =
ằ
SI2 − SA2 =
√
a2 − 2a
2
4
=
a
√
2
2
.
Do đú diện tớch tam giỏc ABC là S∆ABC =
1
2
AI.BC = a2
√
2.
Vậy thể tớch khối chúp S.ABCD là VS.ABC =
1
3
.S∆ABC.SA =
a3
3
.
Cõu 7 (1,0 điểm).
A B
CD
F
K
E
I
P
Đặt AB = a > 0, ta cú :
S∆EFK = SAEKD − S∆AEF − S∆DFK = 12 (AE+ DK) AD−
1
2
AE.AF− 1
2
DF.DK =
5a2
16
(1)
Khoảng cỏch từ F đến EK là d (F, EK) =
∣∣∣∣∣2092 − 24− 18
∣∣∣∣∣√
425
=
25
√
17
34
.
Lại cú EK =
√
a2 +
a2
16
=
a
√
17
4
⇒ S∆EFK = 12EK.d (F, EK) =
1
2
.
a
√
17
4
.
25
√
17
34
=
25a
16
(2).
Từ (1) và (2) ta cú
5a2
16
=
25a
16
⇔ a = 5⇒ EF = 5
√
2
2
(3).
Ta cú E
ầ
t;
19t− 18
8
ồ
⇒ −→EF =
ầ
11
2
− t; 42− 19t
8
ồ
⇒ EF =
425
64
t2 − 575
16
t+
925
16
(4).
Từ (3) và (4) ta cú
425
64
t2 − 575
16
t+
925
16
=
25
2
⇔
 t = 2
t =
58
17
(loại)
⇒ E
ầ
2;
5
2
ồ
.
Gọi I là trung điểm EF ⇒ I
ầ
15
2
;
11
2
ồ
.
Đường thẳng AC qua I
ầ
15
2
;
11
2
ồ
và nhận
−→
EF =
ầ
7
2
;
1
2
ồ
làm vectơ phỏp tuyến.
Do đú AC cú phương trỡnh 7x+ y− 29 = 0.
Gọi P là giao điểm của AC và EK thỡ tọa độ P là nghiệm hệ :
7x+ y− 29 = 019x− 8y− 18 = 0 ⇔

x =
10
3
y =
17
3
⇒ P
ầ
10
3
;
17
3
ồ
3
Ta cú IC =
3
4
AC và PC =
1
3
AC, suy ra IC =
9
4
PC hay
−→
IC =
9
5
−→
IP.
Từ đú suy ra C(3; 8).
Cõu 8 (1,0 điểm).
Đường thẳng d cú phương trỡnh tham số

x = 1+ 2t
y = t
z = t
.
Mặt phẳng (α) cú vectơ phỏp tuyến −→n = (1; 2;−1).
Giả sử ∆ cắt d tại N ⇒ N(1+ 2t; t; t)⇒ −−→MN = (2t; t+ 1; t− 1).
Lại cú ∆||(α) nờn −−→MN.−→n = 0⇔ 2t+ 2(t+ 1)− (t− 1) = 0⇔ t = −1⇒ N(−1;−1;−1).
Đường thẳng ∆ qua M(1;−1; 1) và nhận −−→MN = (−2; 0;−2) làm vectơ chỉ phương.
Do đú ∆ cú phương trỡnh

x = 1− 2t
y = −1
z = 1− 2t
.
Cõu 9 (0,5 điểm).
Chia 20 học sinh thành 4 nhúm nờn số phần tử khụng gian mẫu là |Ω| = C520.C515.C510.C55 .
Gọi A là biến cố "Chia 20 học sinh thành 4 nhúm sao cho 5 bạn nữ thuộc cựng một nhúm".
Xột 5 bạn nữ thuộc một nhúm cú C515.C
5
10.C
5
5 cỏch chia 15 nam vào 3 nhúm cũn lại.
Vỡ 5 bạn nữ cú thể thuộc nhúm A, B,C hay D nờn ta cú |ΩA| = 4.C515.C510.C55 .
Vậy xỏc suất của biến cố A là P (A) =
|ΩA|
|Ω| =
4.C515.C
5
10.C
5
5
C520.C
5
15.C
5
10.C
5
5
=
4
C520
=
1
3876
.
Cõu 10 (1,0 điểm).
Áp dụng bất đẳng thức cộng mẫu số ta cú :
a
b
+
b
c
+
c
a
=
a2
ab
+
b2
bc
+
c2
ca
> (a+ b+ c)
2
ab+ bc+ ca
Do đú ta chỉ cần chứng minh :
(a+ b+ c)2
ab+ bc+ ca
+ a+ b+ c > 6⇔ a+ b+ c+ a
2 + b2 + c2
ab+ bc+ ca
> 4 (1)
Đặt x = a+ b+ c⇒ ab+ bc+ ca = x
2 − 3
2
, bất đẳng thức (1) trở thành :
x+
6
x2 − 3 > 4⇔ x
Ä
x2 − 3ọ+ 6 > 4 Äx2 − 3ọ⇔ (x+ 2)(x− 3)2 > 0 (đỳng ∀x > 0)
Dấu bằng xảy ra khi và chỉ khi a = b = c = 1.
———Hết ———
4