Đề 5 thi thử kỳ thi thpt quốc gia môn : Toán thời gian làm bài 180 phút

NMHIEUPDP.WORDPRESS.COM ĐỀ THI THỬ KỲ THI THPT QUỐC GIA
———————— Mụn : TOÁN
Đỏp ỏn đề số 05 Thời gian làm bài 180 phỳt
————
Cõu 1a (1,0 điểm).
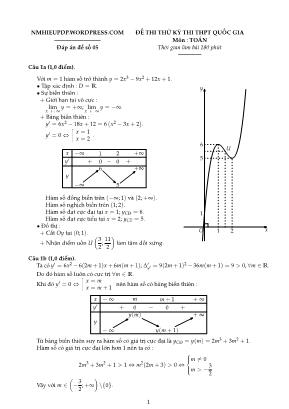
Với m = 1 hàm số trở thành y = 2x3 − 9x2 + 12x+ 1.
• Tập xỏc định : D = R.
• Sự biến thiờn :
+ Giới hạn tại vụ cực :
lim
x→+∞ y = +∞; limx→−∞ y = −∞.
+ Bảng biến thiờn :
y′ = 6x2 − 18x+ 12 = 6 Äx2 − 3x+ 2ọ.
y′ = 0⇔
ủ
x = 1
x = 2 .
x −∞ 1 2 +∞
y′ + 0 − 0 +
y
−∞
6
5
+∞
Hàm số đồng biến trờn (−∞; 1) và (2;+∞).
Hàm số nghịch biến trờn (1; 2).
Hàm số đạt cực đại tại x = 1; yCĐ = 6.
Hàm số đạt cực tiểu tại x = 2; yCT = 5.
• Đồ thị :
+ Cắt Oy tại (0; 1).
+ Nhận điểm uốn U
ầ
3
2
;
11
2
ồ
làm tõm đối xứng.
y
xO
5
1
6
1 2
U
Cõu 1b (1,0 điểm).
Ta cú y′ = 6x2− 6(2m+ 1)x+ 6m(m+ 1); ∆′y′ = 9(2m+ 1)2− 36m(m+ 1) = 9 > 0, ∀m ∈ R.
Do đú hàm số luụn cú cực trị ∀m ∈ R.
Khi đú y′ = 0⇔
ủ
x = m
x = m+ 1 nờn hàm số cú bảng biến thiờn :
x − ∞ m m+ 1 + ∞
y′ + 0 − 0 +
y
− ∞
y(m)
y(m+ 1)
+ ∞
Từ bảng biến thiờn suy ra hàm số cú giỏ trị cực đại là yCĐ = y(m) = 2m3 + 3m2 + 1.
Hàm số cú giỏ trị cực đại lớn hơn 1 nờn ta cú :
2m3 + 3m2 + 1 > 1⇔ m2(2m+ 3) > 0⇔

m 6= 0
m > −3
2
Vậy với m ∈
ầ
−3
2
;+∞
ồ
\{0}.
1
Cõu 2a (0,5 điểm).
Vỡ A, B,C là ba gúc của một tam giỏc nờn A+ B = pi − C. Do đú ta cú :
sin 2A+ sin 2B+ sin 2C = 2 sin (A+ B) cos (A− B) + 2 sinC cosC
= 2 sinC cos (A− B) + 2 sinC cos (A+ B)
= 2 sinC [cos (A− B)− cos (A+ B)]
= −2 sinC.2 sin A sin (−B)
= 4 sin A sin B sinC
Ta cú đẳng thức cần chứng minh.
Cõu 2b (0,5 điểm).
Gọi z = a+ bi, (a, b ∈ R), ta cú :
|z| − 2z = 3 (−1+ 2i)⇔
ằ
a2 + b2 − 2 (a− bi) = −3+ 6i
⇔
ằ
a2 + b2 − 2a+ 2bi = −3+ 6i
⇔
{ √
a2 + b2 − 2a = −3
2b = 6
⇔
{ √
a2 + 9 = 2a− 3
b = 3
⇔

a > 3
2
3a2 − 12a = 0
b = 3
⇔
đ
a = 4
b = 3
Từ đú suy ra z = 4+ 3i. Do đú A = |z|+ |z|2 + |z|3 = 5+ 52 + 53 = 155.
Cõu 3 (0,5 điểm).
Phương trỡnh đó cho tương đương với :
log22 x− log2x− 6 = 0⇔
ủ
log2x = 3
log2x = −2
⇔
 x = 8
x =
1
4
Vậy phương trỡnh cú hai nghiệm x = 8, x = x =
1
4
.
Cõu 4 (1,0 điểm).
Hệ đó cho tương đương với
 x− 1+
√
(x− 1)2 + 1 = 3y−1
y− 1+
√
(y− 1)2 + 1 = 3x−1
.
Đặt
x− 1 = uy− 1 = v , hệ trở thành
{
u+
√
u2 + 1 = 3v (1)
v+
√
v2 + 1 = 3u (2)
.
Trừ theo vế (1) và (2) ta cú u+
√
u2 + 1+ 3u = v+
√
v2 + 1+ 3v (∗).
Xột f (t) = t+
√
t2 + 1+ 3t trờn R cú f ′(t) = 1+ t√
t2 + 1
+ 3t ln 3 > 0, ∀t ∈ R.
Do đú (∗)⇔ f (u) = f (v)⇔ u = v.
Với u = v thay vào (1) được u+
√
u2 + 1 = 3u ⇔ 3u
(√
u2 + 1− u
)
= 1 (∗∗).
Xột g(u) = 3u
(√
u2 + 1− u
)
cú g′(u) = 3u
(√
u2 + 1− u
)ầ
ln 3− 1√
u2 + 1
ồ
> 0, ∀u ∈ R.
Lại cú g(0) = 0 do đú (∗∗) cú nghiệm duy nhất u = 0.
Với u = 0⇒ v = 0⇒ x = y = 1.
Vậy hệ cú nghiệm duy nhất (x; y) = (1; 1).
2
Cõu 5 (1,0 điểm).
Ta cú x+ y = 3⇔ y = 3− x.
Phương trỡnh hoành độ giao điểm x2 + 1 = 3− x ⇔
ủ
x = 1
x = −2 .
Do đú diện tớch hỡnh phẳng cần tỡm là :
S =
1∫
−2
∣∣∣Äx2 + 1ọ− (3− x)∣∣∣ dx = 1∫
−2
Ä−x2 − x+ 2ọ dx = (−x3
3
− x
2
2
+ 2x
)∣∣∣∣∣
1
−2
=
9
2
Vậy diện tớch hỡnh phẳng cần tỡm là S =
9
2
.
Cõu 6 (1,0 điểm).
Ta cú OS =
3
2
OG nờn d(O, (SCD)) =
3
2
.d(G, (SCD)) =
3
2
.
a
√
3
6
=
a
√
3
4
.
Gọi I là trung điểm CD và H là hỡnh chiếu của O trờn SI.
Ta cú CD⊥OI và CD⊥SO nờn CD⊥(SOI)⇒ CD⊥OH mà OH⊥SI nờn OH⊥(SCD).
Khi đú OH = d(O, (SCD)) =
a
√
3
4
.
A
B C
D
O
S
G H
I
Lại cú ∆SOI ∼ ∆SHO⇒ SO = OH.SI
OI
=
a
√
3
4
.
√
SO2 +
a2
4
a
2
.
Hay SO2 =
3
4
(
SO2 +
a2
4
)
⇔ SO = a
√
3
2
.
Mặt khỏc SABCD = a2, do đú VS.ABCD =
1
3
SABCD.SO =
a3
√
3
6
.
Cõu 7 (1,0 điểm).
Tam giỏc ABC cõn tại A nờn HD = HE = 2.
Do đú D, E nằm trờn đường trũn (C) : x2 + y2 + 6x− 4y+ 9 = 0.
Ta cú A ∈ d⇒ A(3a+ 3; a)⇒ −→HA = (3a+ 6; a− 2)⇒ HA = √10a2 + 32a+ 40.
Gọi I trung điểm AH ⇒ I
ầ
3a
2
;
a+ 2
2
ồ
.
Lại cú ữADH = ữAEH = 900 nờn D, E nằm trờn (C′) : x2 + y2 − 3ax− (a+ 2)y− 7a− 9 = 0.
Do đú tọa độ D, E thỏa món hệ
x2 + y2 + 6x− 4y+ 9 = 0 (1)x2 + y2 − 3ax− (a+ 2)y− 7a− 9 = 0 (2) .
3
AB C
H
FDE
I
d
Trừ theo vế (1) và (2) ta cú (3a+ 6)x+ (a− 2)y+ 7a+ 18 = 0 (∗).
Vỡ tọa độ D, E thỏa món (∗) nờn (∗) là phương trỡnh của DE.
Lại cú F ∈ DE nờn ta cú −6a− 12+ 3a− 6+ 7a+ 18 = 0⇔ a = 0⇒ A(3; 0).
Vậy A(3; 0).
Cõu 8 (1,0 điểm).
Mặt cầu (S) cú tõm I(2;−3;−3) và bỏn kớnh R = √4+ 9+ 9− 17 = √5.
Khoảng cỏch từ tõm I đến mặt phẳng (P) là d(I, (P)) =
2+ 6− 6+ 1√
1+ 4+ 4
= 1.
Vỡ d(I, (P)) < R nờn (P) cắt (S) theo giao tuyến là đường trũn cú bỏn kớnh r =
√
5− 1 = 2.
Mặt phẳng (P) cú vectơ phỏp tuyến −−→n(P) = (1;−2; 2).
Gọi K là tõm đường trũn giao tuyến, ta cú IK vuụng gúc với (P).
Do đú IK nhận−−→n(P) = (1;−2; 2) làm vectơ chỉ phương nờn cú phương trỡnh

x = 2+ t
y = −3− 2t
z = −3+ 2t
.
Vỡ K ∈ IK nờn K(2+ t;−3− 2t;−3+ 2t).
Mặt khỏc K ∈ (P) nờn 2+ t− 2(−3− 2t)+ 2(−3+ 2t)+ 1 = 0⇔ t = −1
3
⇒ K
ầ
5
3
;−7
3
;−11
3
ồ
.
Vậy (P) cắt (S) theo giao tuyến là đường trũn cú tõm K
ầ
5
3
;−7
3
;−11
3
ồ
và bỏn kớnh r = 2.
Cõu 9 (0,5 điểm).
Chọn khối thi thỏa món yờu cầu bài toỏn cú hai trường hợp sau :
TH1 : Khối thi cú cả Toỏn và Văn.
Hai mụn thi đầu tiờn chọn Toỏn và Văn nờn cú 1 cỏch chọn.
Mụn thi thứ ba chọn 1 trong 6 mụn cũn lại nờn cú 6 cỏch chọn.
Do đú trường hợp này cú 1ì 6 = 6 khối thi.
TH2 : Khối thi chỉ cú Toỏn hoặc Văn.
Mụn thi thứ nhất chọn Toỏn hoặc Văn nờn cú 2 cỏch chọn.
Hai mụn thi cũn lại chọn trong 6 mụn cũn lại nờn cú C26 = 15 cỏch chọn.
Do đú trường hợp này cú 2ì 15 = 30 khối thi.
Vậy trường đại học X cú thể cú 6+ 30 = 36 khối thi.
Cõu 10 (1,0 điểm).
Ta cú
a2 + 1
4b2
+
b2 + 1
4c2
+
c2 + 1
4a2
> a
2b2
+
b
2c2
+
c
2a2
.
Lại cú
a
b2
+
1
a
> 2
b
;
b
c2
+
1
b
> 2
c
;
c
a2
+
1
c
> 2
a
⇒ a
b2
+
b
c2
+
c
a2
> 1
a
+
1
b
+
1
c
.
Từ đú suy ra
a2 + 1
4b2
+
b2 + 1
4c2
+
c2 + 1
4a2
> 1
2
ầ
1
a
+
1
b
+
1
c
ồ
.
Hay
a2 + 1
4b2
+
b2 + 1
4c2
+
c2 + 1
4a2
> 1
4
ủầ
1
a
+
1
b
ồ
+
ầ
1
b
+
1
c
ồ
+
ầ
1
c
+
1
a
ồụ
> 1
a+ b
+
1
b+ c
+
1
c+ a
.
Ta cú bất đẳng thức cần chứng minh.
———Hết ———
4