Đề 3 thi thử thpt quốc gia năm 2015 môn thi: Toán 12 thời gian làm bài: 180 phút

Trường THPT Nguyễn Diêu
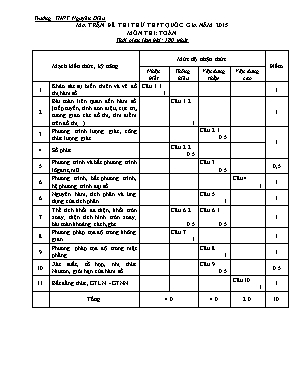
MA TRẬN ĐỀ THI THỬ THPT QUỐC GIA NĂM 2015
MÔN THI: TOÁN
Thời gian làm bài: 180 phút 
Mạch kiến thức, kỹ năng
Mức độ nhận thức
Điểm
Nhận biết
Thông hiểu
Vận dụng thấp
Vận dụng cao
1
Khảo sát sự biến thiên và vẽ đồ thị hàm số
Câu 1.1
1
1
2
Bài toán liên quan đến hàm số (tiếp tuyến, tính đơn điệu, cực trị, tương giao các đồ thị, tìm điểm trên đồ thị...)
Câu 1.2
1
1
3
Phương trình lượng giác, công thức lượng giác
Câu 2.1
0.5
1
4
Số phức
Câu 2.2
0.5
5
Phương trình và bất phương trình lôgarit, mũ.
Câu 3
0.5
0,5
6
Phương trình, bất phương trình, hệ phương trình đại số.
Câu 4
1
1
6
Nguyên hàm, tích phân và ứng dụng của tích phân
Câu 5
1
1
7
Thể tích khối đa diện, khối tròn xoay; diện tích hình tròn xoay; bài toán khoảng cách, góc.
Câu 6.2
0.5
Câu 6.1
0.5
1
8
Phương pháp tọa độ trong không gian
Câu 7
1
1
9
Phương pháp tọa độ trong mặt phẳng
Câu 8
1
1
10
Xác suất, tổ hợp, nhị thức Niutơn, giới hạn của hàm số
Câu 9
0.5
0.5
11
Bất đẳng thức, GTLN - GTNN
Câu 10
1
1
Tổng
4.0
4.0
2.0
10
Trường THPT Nguyễn Diêu 
ĐỀ THI THỬ THPT QUỐC GIA NĂM 2015
MÔN THI: TOÁN
Thời gian làm bài: 180 phút 
Câu 1 (2,0 điểm). Cho hàm số (1).
Khảo sát sự biến thiên và vẽ đồ thị của hàm số (1).
Viết phương trình tiếp tuyến với đồ thị tại điểm M có hoành độ 
Câu 2 (1,0 điểm). 
Giải phương trình .
Tìm phần thực và phần ảo của số phức biết z thỏa mãn điều kiện
Câu 3 (0,5 điểm). Giải phương trình 
Câu 4 (1,0 điểm). Giải hệ phương trình .
Câu 5 (1,0 điểm). Tính tích phân 
Câu 6 (1,0 điểm). Cho hình chóp có đáy là hình vuông cạnh bằng . lần lượt là trung điểm của và , là giao điểm của và . Biết vuông góc với mặt phẳng và góc giữa đường thẳng và mặt phẳng bằng . Tính thể tích khối chóp và khoảng cách giữa hai đường thẳng , . 
Câu 7 (1,0 điểm). Trong mặt phẳng với hệ toạ độ Oxy, cho hình vuông . Điểm thuộc đoạn thẳng , các điểm và lần lượt là hình chiếu vuông góc của điểm trên và . Xác định toạ độ các đỉnh của hình vuông 
Câu 8 (1,0 điểm). Trong không gian với hệ tọa độ Oxyz, cho điểm A(-1;0;0) và đường thẳng d có phương trình Lập phương trình mặt phẳng (P) đi qua A và vuông góc với đường thẳng d. Từ đó suy ra tọa độ điểm H là hình chiếu vuông góc của A lên đường thẳng d.
Câu 9 (0,5 điểm). Từ các chữ số 0; 1; 2; 3; 4; 5 có thể lập được bao nhiêu số tự nhiên có 5 chữ số và số đó chia hết cho 3? 
Câu 10 (1,0 điểm). Cho ba số thực thoả mãn: . Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức 
--------------------Hết--------------------
ĐÁP ÁN THI THỬ THPT QUỐC GIA II NĂM 2015
MÔN : TOÁN
CÂU
Ý
NỘI DUNG
ĐIỂM
1
1
1đ
+ TXĐ: 
+ Sự biến thiên:
Chiều biến thiên: . 
Vậy hàm số nghịch biến trên mỗi khoảng: và (0;1) ;
 đồng biến trên mỗi khoảng (-1;0) và .
Cực trị:
Hàm số đạt cực đại tại x = 0, ycđ = 0.
Hàm số đạt cực tiểu tại , yct = - 1.
Giới hạn : 
Bảng biến thiên : 
 x
 -1 0 1 
 y/ 
 - 0 + 0 - 0 +
 y
 0 
 -1 -1
+ Đồ thị: 
 - Giao điểm với Ox : (0; 0); 
 - Giao điểm với Oy : (0 ; 0)
Nhận xét : Đồ thị nhận trục Oy làm trục đối xứng.
0,25
0,25
0,25
2
1đ
Với x0 = , y0 = 0, 
Pttt là 
0,5
0,5
2
1
0,5đ
Với 
Với 
0.25
0.25
2
0,5đ
Gỉa sử suy ra 
Thế vào gt ta tìm được x= 3, y = 4.
Vậy z = 3 +4i. Do đó w = 3i
w có phần thực 0; phần ảo 3. 
0,25
0,25
3
0,5đ
 Gpt: (1) 
Đk: x>0. Pt (1) 
 KL: Vậy tập nghiệm pt (1) là 
0,25
0,25
4
1đ
ĐK:
 Thay y=x-2 vao (2) được
Xét f(x)=VT(*) trên [-2;21/3],có f’(x)>0 nên hàm số đồng biến. suy ra x=-1 là nghiệm duy nhất của (*)
KL: HPT có 2 nghiệm (2;0),(-1;-3) 
0,5
0,25
0,25
5
1đ
Tính M
 Đặt 
Tính N
 Đặt 
 Đổi cận 
Vậy 
0,25
0,25
0,25
6
1
1đ
Do là hình vuông cạnh nên .
 là hình chiếu vuông góc của trên mp
Mà: Nên 
Trong có: 
Thể tích của khối chóp là: (đvtt)
Trong mp kẻ tại ..
Trong có: Có : 
Trong có: 
 Vậy 
0,25
0,25
0,25
0,25
7
1đ
Ta có: 
Giả sử , là VTPT của đường thẳng .
Có: nên: 
Với , chọn 
 nằm trên đoạn (thỏa mãn)
Khi đó: 
Với , chọn .
 nằm ngoài đoạn (L) Vậy: 
0,25
0,25
0,25
0,25
8
1đ
+) d có 1 VTCP là 
+) (P) qua A(-1;0;0) và có VTPT có pt : x + 2y + z +1 = 0.
+) H là giao điểm của (d) và (P) nên tọa độ H là nghiệm của hệ pt
 Vậy H(1;-1;0).
 0,25
0,5
0,25
9
0,5đ
Số có 5 chữ số cần lập là (; a, b, c, d, e{0; 1; 2; 3; 4; 5})
- Nếu thì chọn e = 0 hoặc e = 3
- Nếu chia 3 dư 1 thì chọn e = 2 hoặc e = 5
- Nếu chia 3 dư 2 thì chọn e = 1 hoặc e = 4
Như vậy với mỗi số đều có 2 cách chọn e để được một số có 5 chữ số chia hết cho 3
Số các số dạng lập được từ tập A là: 5x6x6x6= 1080 số
Số các số cần tìm là 2 x 1080 = 2160 số
0,25
0,25
10
1đ
Trong không gian với hệ tọa độ . Xét mặt cầu:
. Có tâm ,bán kính .
Xét mp 
G/s . Từ có điểmnằm bên trong và kể cả trên mặt cầu 
Với thì là giao điểm của mp: 
 Và đường thẳng đi qua và .
Với . Tương tự 
Vậy khi khi 
0,25
0,25
0,25
0,25
* Chú ý: Mọi cách giải khác đúng đều đạt điểm tối đa.