Chuyên đề Lượng giác luyện thi THPT Quốc gia

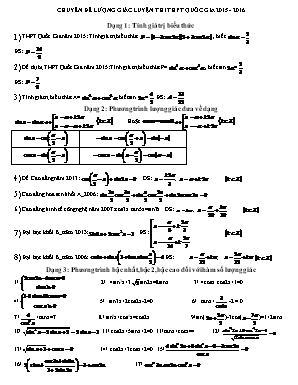
CHUYÊN ĐỀ LƯỢNG GIÁC LUYỆN THI THPT QUỐC GIA 2015 - 2016
Dạng 1: Tính giá trị biểu thức
THPT Quốc Gia năm 2015: Tính giá trị biểu thức , biết 
ĐS: 
Đề dự bị THPT Quốc Gia năm 2015: Tính giá trị biểu thức P=, biết sin=
ĐS: 
Tính giá trị biểu thức A= biết sin= ĐS: 
Dạng 2: Phương trình lượng giác đưa về dạng
 Hoặc 
Đề Cao đẳng năm 2013: ĐS: ; 	
Cao đẳng hoa sen khối A_2006: 
Cao đẳng kinh tế công nghệ năm 2007: cos3x.tan5x=sin7x ĐS: ; 	
Đại học khối B_năm 2013: ĐS: 	
Đại học khối B_năm 2006: ĐS:	; 	
Dạng 3: Phương trình bậc nhất,bậc 2, bậc cao đối với hàm số lượng giác
1/ 2/ 4sin3x+3sin2x=8sinx 3/ 4cosx.cos2x +1=0 
4/ 5/ sin3x+2cos2x-2=0 6/ tanx+ -2 = 0 
7 /+tanx=7 8 / sin6x+cos4x=cos2x 9/sin()-3cos()=1+2sinx 10/ 11/ cos2x+5sinx+2=0 11/ tanx+cotx=4 12/ 
13/ 14/ cos2x+3cosx+2=0 15/ 
16/ 17/ 
 18/ 19/
Cao đẳng năm 2011: ĐS: 	(kZ)
Cao đẳng năm 2010: ĐS: ; 	(kZ)
Cao đẳng Xây Dựng 2 năm 2007: ĐS: ; (kZ)
Cao đẳng Xây Dựng 2 năm 2005: ĐS: ; ; 
Cao đẳng kinh tế kỹ thuật cn2 năm 2005: ĐS: 	
Đại học khối A_năm 2006 ĐS: (m)
Đại học khối D_năm 2005: ĐS: 
Đại học khối B_năm 2004: ĐS: ; 	(kZ)
Đại học khối B_năm 2003: ĐS: 
Đại học khối A_năm 2002 Tìm nghiệm thuộc của phương trình 
ĐS: ; 
ĐH sài gòn khối A năm 2007: ĐS: 	(kZ)
ĐH sài gòn khối DM năm 2007: ĐS: 	(kZ)
Đại học thủy sản TPHCM 2001: ĐS: ; 	
Đại học thủy sản nha trang năm 2001: ĐS: 	
 Dạng 4: Phương trình bậc nhất đối với sinx và cosx: asinx+bcosx=c
Lưu ý:
 Điều kiện pt có nghiệm: 
Giải các pt sau:
1/ 2sin15x+cos5x+sin5x=k với k=0, k=4 2/ 3/ 4/ 
5/ tìm nghiệm 
6/( cos2x-sin2x)- sinx-cosx+4=0 7/ 
 ĐS: hoặc 	(kZ)
 ĐS: hoặc 	(kZ)
 ĐS: hoặc 	(kZ)
ĐS: 	(kZ)
3sinx-4cosx=6 ĐS: PTVN
Cao đẳng xây dựng 2 năm 2006: ĐS: ; (kZ)
CĐ gtvt3 năm 2006: ĐS: 	(kZ)
Cao đẳng kỹ thuật cần thơ năm 2006: ĐS: 	(kZ)
Đại học khối D_năm 2007 
ĐS: 	(kZ)
Đại học sư phạm TPHCM năm 2001: 
ĐS: 	(kZ)
Học viện bưu chính viễn thông năm 2001: 
ĐS: ;	(kZ)
Đại học khối B_năm 2012: 
ĐS: 	
Đại học khối A_năm 2009 ĐS: 	(kZ)
Cao đẳng năm 2008: ĐS: ; 	(kZ)
Cao đẳng giao thông vận tải 3 năm 2007: 
ĐS: 	(kZ)
Cao đẳng sư Phạm TPHCM năm 2005: 
ĐS: 	(kZ)
Cao đẳng công nghiệp 4 năm 2004: 
ĐS: 	(kZ)
Đại học khối B_năm 2009 
ĐS: 	(kZ)
Đại học khối D_năm 2009 
ĐS: 	(kZ)
Dạng 5: Phương trình đẳng cấp đối với sinx và cosx
1/a/ 3sin2x- sinxcosx+2cos2x cosx=2 b/ 4 sin2x+3sinxcosx-2cos2x=4
 c/3 sin2x+5 cos2x-2cos2x-4sin2x=0 d/ 2 sin2x+6sinxcosx+2(1+ )cos2x-5-=0
2/ sinx- 4sin3x+cosx=0 2 c¸ch +/ (tanx -1)(3tan2x+2tanx+1)=0 
3/ tanx sin2x-2sin2x=3(cos2x+sinxcosx) 4/ 3cos4x-4sin2xcos2x+sin4x=0 5/ 4cos3x+2sin3x-3sinx=0 
6/ 2 cos3x= sin3x 7/ cos3x- sin3x= cosx+ sinx 8/ sinx sin2x+ sin3x=6 cos3x 9/sin3(x-/4)=sinx 
Cao đẳng kỹ thuật cao thắng năm 2006: 
ĐS: ; 	(kZ)
Cao đẳng kỹ thuật cao thắng năm 2007: ĐS: 	(kZ)
Đại học bách khoa hà nội năm 2001: ĐS: 	(kZ)
Cao đẳng sư phạm TP HCM năm 2001:2sin2x=3tanx+1 ĐS: 	(kZ)
Dạng 6: Phương trình đối xứng và phản đối xứng
1/ a/1+tanx=2sinx + b/ sin x+cosx=- 2/ sin3x+cos3x=2sinxcosx+sin x+cosx 3/ 1- sin3x+cos3x= sin2x 4/ 2sinx+cotx=2 sin2x+1 5/sin2x(sin x+cosx)=2 
 6/ (1+sin x)(1+cosx)=2 7/(sin x+cosx)=tanx+cotx 8/1+sin3 2x+cos32 x=sin 4x 
9/* a* 3(cotx-cosx)-5(tanx-sin x)=2 9/b*: cos4x+sin4x-2(1-sin2xcos2x) sinxcosx-(sinx+cosx)=0
10/ 11/ cosx++sinx+= 12/ sinxcosx+=1 
Cao đẳng Sư Phạm TWTPHCM năm 2007: 
Đại học khối A_năm 2012: 
Đại học khối D_năm 2012: 
Đại học khối A_năm 2011: 
Đại học khối B_năm 2010:
Đại học khối D_năm 2010: 
Đại học nông nghiệp I năm 2001: 
Dạng 7: Phương trình lượng giác giải bằng phương pháp hạ bậc
1/ sin2 x+sin23x=cos22x+cos24x 2/ cos2x+cos22x+cos23x+cos24x=3/2
3/sin2x+ sin23x-3 cos22x=0 4/ cos3x+ sin7x=2sin2()-2cos2
5/ sin24 x+ sin23x= cos22x+ cos2x với 6/sin24x-cos26x=sin() với 7/ cos4x-5sin4x=1 8/4sin3x-1=3-cos3x 9/ sin22x+ sin24x= sin26x 10/ sin2x= cos22x+ cos23x 11/ (sin22x+cos42x-1):=0 12/ 4sin3xcos3x+4cos3x sin3x+3 cos4x=3 
13/ 2cos22x+ cos2x=4 sin22xcos2x 14/ cos4xsinx- sin22x=4sin2()-7/2 với <3 
15/ 2 cos32x-4cos3xcos3x+cos6x-4sin3xsin3x=0 16/ sin3xcos3x +cos3xsin3x=sin34x 
17/ * 8cos3(x+)=cos3x 18/cos10x+2cos24x+6cos3xcosx=cosx+8cosxcos23x 
19 / cos7x+ sin22x= cos22x- cosx 20/ sin2x+ sin22x+ sin23x=3/2 21/ 3cos4x-2 cos23x=1
Dạng 8: Phương trình lượng giác đưa về dạng tích A.B=0
1/ cos2x- cos8x+ cos4x=1 2/sinx+2cosx+cos2x-2sinxcosx=0 3/sin2x-cos2x=3sinx+cosx-2 4/sin3 x+2cosx-2+sin2 x=0 5/ 3sinx+2cosx=2+3tanx 6/ sin2x+cos2x+cosx=0 
7/ 2sin2x-cos2x=7sinx+2cosx-4 8/ 9/ 2cos2x-8cosx+7= 10/ cos8x+sin8x=2(cos10x+sin10x)+cos2x 11/ 1+ sinx+ cos3x= cosx+ sin2x+ cos2x 
12/ 1+sinx+cosx+sin2x+cos2x=0 13/ sin2 x(tanx+1)=3sinx(cosx-sinx)+3 14/ 2sin3x-=2cos3x+ 15/cos3x+cos2x+2sinx-2=0 16/cos2x-2cos3x+sinx=0 17/ tanx–sin2x-cos2x+2(2cosx-)=0 
18/sin2x=1+cosx+cos2x 19/1+cot2x= 20/ 2tanx+cot2x=2sin2x+ 21/cosx(cos4x+2)+ cos2x-cos3x=0 22/ 1+tanx=sinx+cosx 23/ (1-tanx)(1+sin2x)=1+tanx 
24/ 2= 25/ 2tanx+cotx= 26/ cotx-tanx=cosx+sinx 
Cao đẳng 2012: ĐS: ; 	
Cao đẳng năm 2009: ĐS: ; ;
Cao đẳng kinh tế TPHCM năm 2007: 
Cao đẳng công nghiệp thực phẩm_năm 2007: ĐS: 	
Cao đẳng công nghiệp thực phẩm_năm 2006: ; 	
CDSP TPHCM năm 2006: ĐS: 	
Cao đẳng ktcn1_năm 2006: 
Cao đẳng xây dựng số 3_năm 2006: ĐS: ; 	
Cao đẳng tài chính hải quan năm 2007: ĐS: ; 	(kZ)
Cao đẳng tài chính hải quan năm 2006: ĐS: ; 
Cao đẳng kinh tế kỹ thuật cn2 năm 2007: ĐS: 
Cao đẳng giao thông vận tải 3_năm 2005: ĐS: 	
Đại học khối A_năm 2014: sinx+4cosx=2+sin2x ĐS: 	
Đại học khối B_năm 2014: ĐS: 	
Đại học khối A_năm 2013: ĐS: ; 	
Đại học khối D_năm 2013: ĐS: , ; 
Đại học khối B_năm 2011: sin2x.cosx+sinx.cosx=cos2x+sinx+cosx ĐS: 
Đại học khối D_năm 2011: ĐS: 	(kZ)
Đại học khối A_năm 2010:
Đại học khối A_năm 2008 
Đại học khối D_năm 2008 
ĐS: 	(kZ)
Đại học khối B_năm 2007 
ĐS: 	(kZ)
Đại học khối B_năm 2005: ĐS: 	(kZ)
Đại học khối D_năm 2004: ĐS: ; 	
Đại học sài gòn khối B năm 2007: ĐS: 	(kZ)
Đại học sư phạm quy nhơn năm 2001: sin3x+sin5x=sin4x ĐS: ; 	(kZ)
Đại học kiến trúc TP HCM năm 2001: sinx+sin2x+sin3x=0 ĐS: ; 	(kZ)
Đại học thủy lợi năm 2001: Hướng dẫn đặt 
ĐS: ; ; 	(kZ)
Đại học khối A_năm 2007 
ĐS: 	(kZ)
Đại học khối D_năm 2003: ĐS:	; 	 
Đại học sư phạm kỹ thuật năm 2001: 
ĐS: ; ; 
Đại học khối D_năm 2006: ĐS: ; 	
Đại học khối B_năm 2002: ĐS:	 ; (kZ) 
Đại học nông lâm 2001: 
ĐS: , ; 	(kZ)
Đại học khối D_năm 2002:Tìm nghiệm x thuộc đoạn [0;14] nghiệm đúng phương trình ĐS: ; ; ; 
Dạng 9: Sử dụng hằng đẳng thức để giải pt
1/ sin4+cos4=1-2sinx 2/ cos3x-sin3x=cos2x-sin2x 3/ cos3x+ sin3x= cos2x 4/ 5/cos6x-sin6x=cos22x 6/sin4x+cos4x= 7/ cos6x+sin6x=2(cos8x+sin8x) 8/cos3x+sin3x=cosx-sinx 
9/ cos6x+sin6x=cos4x 10/ sinx+sin2x+sin3x+sin4x= cosx+cos2x+cos3x+cos4x 
11/ cos8x+sin8x= 12/ (sinx+3)sin4-(sinx+3) sin2+1=0 
Dạng 10: Sử dụng công thức lượng giác giải pt
1/ sin3xcosx=+ cos3xsinx 2/ cosxcos2xcos4xcos8x=1/16 3/tanx+2cot2x=sin2x 4/sin2x(cotx+tan2x)=4cos2x 5/ sin4x=tanx 6/ sin2x+2tanx=3 7/ sin2x+cos2x+tanx=2 
8/tanx+2cot2x=sin2x 9/ cotx=tanx+2cot2x 10/a* tan2x+sin2x=cotx b* (1+sinx)2= cosx 
11/ sin8x+ cos4x=1+2sin2xcos6x 12/cosx+cos2x+cos3x+cos4x=0 13/ 14/ sinx+sin2x+sin3x+sin4x=0 15/ sin5x+ sinx+2sin2x=1 1 6/ 
17/ tanx+ tan2x= tan3x 18/ sin()=sin() 19/ sin()=sin2x sin() 
20/(cos4x/3 – cos2x):=0 21/ cosx-2sin()=3 22/ cos()=sin(4x+3) 23/3cot2x+2sin2x=(2+3)cosx 24/2cot2x++5tanx+5cotx+4=0 25/ cos2x+=cosx+ 
26/sinx- cos2x++2=5 27/+2=3 
	Đừng bi quan khi mình không lối thoát,
	Đừng chán nản khi dồn dập khó khăn,
	Đừng thờ ơ khi mình mang tủi nhục,
	Cố gắng kiên trì tất cả sẽ thành công.
 .