Ôn tập môn Toán học - Bài tập về tứ giác nội tiếp

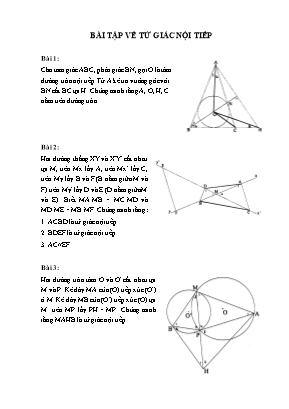
BÀI TẬP VỀ TỨ GIÁC NỘI TIẾP
Bài 1:
Cho tam giác ABC, phân giác BN, gọi O là tâm đường tròn nội tiếp. Từ A kẻ tia vuông góc với BN cắt BC tại H. Chứng minh rằng A, O, H, C nằm trên đường tròn.
Bài 2:
Hai đường thẳng XY và X’Y’ cắt nhau tại M, trên Mx lấy A, trên Mx’ lấy C, trên My lấy B và F (B nằm giữa M và F) trên My’ lấy D và E (D nằm giữa M và E). Biết MA.MB = MC.MD và MD.ME = MB.MF. Chứng minh rằng:
1. ACBD là tứ giác nội tiếp.
2. BDEF là tứ giác nội tiếp.
3. AC//EF
Bài 3:
Hai đường tròn tâm O và O’ cắt nhau tại M và P. Kẻ dây MA của (O) tiếp xúc (O’) ở M. Kẻ dây MB của (O’) tiếp xúc (O) tại M. trên MP lấy PH = MP. Chứng minh rằng MAHB là tứ giác nội tiếp.
Bài 4:
Hai đường tròn tâm O1 và O2 cắt nhau tại A và B. Một cát tuyến qua A cắt (O1) tại P và cắt (O2) tại Q. Vẽ tiếp tuyến Px với (O1), trên tiếp tuyến lấy T, kẻ TQ cắt (O2) tại R. Chứng minh rằng P, T, R, B cùng thuộc một đường tròn.
Bài 5:
Cho hình thang ABCD nội tiếp đường tròn tâm O (AB//CD). AC cắt BD tại E, AD cắt BC tại F. Chứng minh rằng:
1. A, D, O, E thuộc 1 đường tròn
2. AOCF nội tiếp
Bài 6:
Trong góc nhọn AOB lấy điểm C, kẻ CD ^ OA, CE ^ OB, từ D và E kẻ EM ^ OA, DN ^ OB. Chứng tỏ OC ^ MN.
Bài 7:
Trên đường thẳng XY lấy điểm C cố định, kẻ CZ ^ XY, trên CZ lấy A, B cố định sao cho A ở giữa C và B, M chạy trên XY. Hai tia At kẻ vuông góc với AM và Bm vuông góc với BM cắt nhau tại P. Chứng minh rằng:
1. MABP nội tiếp.
2. Tâm O của đường tròn ngoại tiếp MABP di động trên 1 đường thẳng cố định rồi suy ra hình chiếu vuông góc của P xuống CZ là 1 điểm cố định.
3. Tia BM cắt AP tại H. Tia PB cắt tia MA ở K. Chứng minh rằng KH ^ PM
4. Gọi N và E là trung điểm của KH và AB. Chứng minh rằng N, E, O thẳng hàng.
Bài 8:
Cho điểm A thuộc đường tròn (O) và tiếp tuyến Ax. Trên Ax lấy C. Gọi B là trung điểm của AC. Kẻ các cát tuyến BEF.CE và CF cắt (O) tại M và N.
1. Chứng tỏ tam giác AEB ~ FAB.
2. Vẽ hình bình hành AECD. Chứng minh AFCD là tứ giác nội tiếp.
3. Chứng minh MN ^ OA.
Bài 9:
Cho tam giác ABC có góc A bằng 600. Phân giác BE và CF cắt nhau tại D. Chứng minh rằng DE = DF.
Bài 10:
Cho 1 góc xOy, trên phân giác của góc lấy I và lấy A, B trên Ox. Các đường tròn qua O, I cắt Ox tại A và cắt Oy tại C, một đường tròn thứ 2 qua OI cắt Ox tại B và Oy tại D. Chứng minh CD = AB.
Bài 11:
Cho (O) có 2 đường kính AE ^ BF. Lấy C trên cung EF, CA và CB cắt BF và AE lần lượt tại P, Q, EF cắt AC tại D. Chứng minh QD//BF.
Bài 12:
Hai đường tròn (O1, R1) và (O2, R2) cắt nhau tại M và P, tiếp tuyến tại M của đường tròn (O1) cắt (O2) tại B, tiếp tuyến tại M của (O2) cắt (O1) tại A. Kéo dài MP thêm một đoạn PH = MP. Từ O1 kẻ đường thẳng ^ MA và từ O2 kẻ đường thẳng ^ MB, 2 đường thẳng này cắt nhau tại S. Chứng minh:
1. SP//O1O2
2. SM//SH
3. MAHB là tứ giác nội tiếp 
Bài 13:
Cho hai đường tròn (O1) và (O2) cắt nhau tại A và B, trên cung AB của (O1) lấy C, BC cắt (O2) tại D, AC cắt (O2) tại E, AD cắt (O1) tại F, FC cắt DE tại K. Chứng minh:
1. FAKE nội tiếp
2. FDKB nội tiếp
3. BCKE nội tiếp
Bài 14:
Cho góc vuông xOy, trên Ox lấy A, trên Oy lấy B sao cho OA = OB. Vẽ đường tròn tâm O1 tiếp xúc Ox tại A và cắt AB tại M. Vẽ đường tròn O2 đi qua B, M và tiếp xúc Oy tại B. Hai đường tròn (O1) và (O2) cắt nhau tại N. Chứng minh:
1. O1MO2N là tứ giác nội tiếp
2. OANB là tứ giác nội tiếp
3. O1A cắt O2B tại D. Chứng minh tứ giác ANDB nội tiếp
Bài 15:
Cho tam giác ABC nội tiếp đường tròn tâm O. Trên cung AC lấy M, kẻ MH, MK, MI lần lượt vuông góc với AB, AC, BC. Chứng minh rằng H, K, I thẳng hàng.
Bài 16:
Cho tam giác ABC nội tiếp đường tròn tâm O, đường thẳng ^ OA cắt AB và AC tại M, N. Chứng minh rằng BCNM là tứ giác nội tiếp.
Bài 17: 
Cho tam giác ABC có đường phân giác trong BE hợp với cạnh AC một góc 450 (góc BEA 450). Vẽ đường cao AD của tam giác ABC. Chứng minh góc EDC = 450.
Bài 18:
Cho đường tròn (O) đường kính BC, A là một điểm trên đường tròn kẻ AD vuông góc BC, gọi E, F là tâm đường tròn nội tiếp tam giác ADB và ADC. EF cắt AB và AC tại G và H. Chứng minh BGED, DFHC, EDHA, AFDG là tứ giác nội tiếp.
Bài 19: 
Cho tam giác ABC có O là tâm đường tròn nội tiếp, (O) tiếp xúc AB và AC lần lượt tại D và E, BO và CO cắt DE lần lượt tại M và N. Chứng minh CMEO, BNMC là tứ giác nội tiếp.
Bài 20:
Cho đường tròn tâm O dây AB, I là trung điểm của AB qua I kẻ 2 dây cung CD và EF (C và E thuộc cung AB nhỏ) CF và ED cắt AB lần lượt tại M và N. Chứng minh IM = IN.
Bài 21:
Cho tam giác ABC. Trên BC lấy D bất kỳ, vẽ đường tròn O1 tiếp xúc AB tại B và đi qua D, vẽ đường tròn O2 tiếp xúc AC tại C và đi qua D. Hai đường tròn cắt nhau tại D và E. Chứng minh: Khi D di động trên BC thì DE luôn đi qua một điểm cố định.
Bài 22:
Cho đường tròn tâm O và một điểm A bên ngoài đường tròn, vẽ 2 tiếp tuyến AB và AC (B, C là 2 tiếp điểm), BC cắt OA tại D, trên cung nhỏ BC lấy E, ED cắt (O) tại F. Chứng minh: .
Bài 23:
Cho đường tròn tâm O đường kính BC. Lấy A trên (O) sao cho AB > AC. Vẽ hình vuông ABDE bên ngoài D ABC. AD cắt đường tròn tại F. CF cắt DE tại K. Chứng minh BK là tiếp tuyến của (O).
Bài 24:
Tứ giác ABCD nội tiếp đường tròn (O). Gọi E, F, G, H lần lượt là tâm đường tròn nội tiếp các tam giác ABD, ACD, ABC, BCD. Chứng minh EFGH là hình chữ nhật.
Bài 25:
Cho tam giác cân ABC, O là tâm đường tròn nội tiếp tam giác. M, N là trung điểm của AB và AC. AO cắt MN tại H. P và I là tiếp điểm của đường tròn với cạnh AC, BC. Chứng minh P, H, I thẳng hàng.
Bài 26:
Từ điểm S bên ngoài đường tròn (O) vẽ các tiếp tuyến SA và SB. Vẽ cát tuyến SMN cắt (O) tại M và N (M nằm giữa S và N). Kẻ OI ^ MN. Chứng minh: . 
Bài 27:
Cho tam giác nhọn ABC, các đường cao AA’, BB’, CC’ cắt nhau tại H. Gọi K là trung điểm của AH. I là giao điểm của AH và B’C’. Chứng minh rằng I là trực tâm của tam giác KBC (Lấy L đối xứng H qua BC).
Bài 28: 
Cho tam giác ABC, bên ngoài tam giác, dựng các tam giác đều ABD, ACE, BCF, chứng tỏ BE, CD, AF đồng quy tại một điểm.
Bài 29:
Cho tứ giác ABCD nội tiếp đường tròn tâm O, (góc A>900). Từ A lần lượt kẻ đường thẳng vuông góc AB và AD cắt CD và CB tại M và N. Chứng minh M, N, O thẳng hàng.
Bài 30:
Cho đường tròn tâm O đường kính AB, lấy điểm M trên tiếp tuyến Ax. Qua M kẻ đường thẳng cắt đường tròn tại C và D, BC và BD cắt MO lần lượt tại E và F. Chứng minh OE = OF.
Bài 31:
Cho tam giác ABC nội tiếp đường tròn tâm O. Lấy M trên cung AC, kẻ MH và MK lần lượt vuông góc AC và BC. Gọi I và J lần lượt là trung điểm của AB và HK. Chứng minh IJ vuông góc MJ.
Bài 32:
Cho đường tròn tâm O đường kính AB và điểm C trên đường tròn. Gọi D là trung điểm cung BC. Lấy điểm E trên OB. DE cắt đường tròn tại F. Từ E kẻ đường thẳng song song AC cắt CF tại I. Chứng minh tam giác EBI cân.
Bài 33:
Cho tam giác ABC có ba góc nhọn. Kẻ AD vuông góc BC. Kẻ DE và DF lần lượt vuông góc AB và AC. Lấy E’ và F’ là điểm đối xứng của D qua AB và AC, E’F’ cắt AB và AC lần lượt tại G và H. Chứng minh AD, BH, GC đồng quy.
Bài 34:
Cho hai đường tròn (O) và (O’) cắt nhau tại A và B. Trên AB lấy D vẽ 2 dây EF của (O) và dây MN của (O’) cùng đi qua D. Chứng minh 4 điểm M, N, E, F cùng thuộc một đường tròn.
Bài 35: 
Cho đường tròn (O, R) đường kính AB. Trên AB lấy điểm O’. Vẽ đường tròn (O’, R’) tiếp xúc trong với (O) tại A. Vẽ tiếp tuyến qua B tiếp xúc (O’) tại C và cắt (O) tại E. Kẻ EH và CK vuông góc AB. Chứng minh EK là phân giác góc HEC.
Bài 36:
Cho đường tròn tâm O và O’ cắt nhau tại A và B với O thuộc đường tròn tâm O’. Vẽ cát tuyến cắt (O) và (O’) tại C và D. Chứng minh tam giác BCD cân.
Bài 37:
Cho tam giác vuông ABC (). M là trung điểm BC, trung trực của BC cắt C tại D. Lấy E đối xứng với D qua A, MA cắt BE tại N. Chứng minh tứ giác NEMC nội tiếp.
Bài 38:
Cho hình bình hành BCD có góc A nhọn, AB < AD. Tia phân giác góc BAD cắt BC tại M và cắt DC tại N. Gọi K là tâm đường tròn ngoại tiếp tam giác MCN.
1. Chứng minh DN = BC và CK ^ MN
2. Chứng minh BKCD là tứ giác nội tiếp
3. Đường thẳng (D BDC) cắt (K) ở H. Chứng minhn CH ^ AH
Bài 39:
Cho tam giác ABC nhọn có H là trực tâm, gọi M và N là trung điểm của AB và CH, phân giác góc CAH và phân giác góc CBH cắt nhau tại P. Chứng minh rằng M, N, P thẳng hàng.
Bài 40:
Cho tam giác ABC nhọn có góc A = 450 nội tiếp đường tròn O, BE và CF là 2 đường cao cắt nhau tại H, gọi M và K lần lượt là trung điểm của BC và AH.
1. Chứng minh MEKF là hình vuông.
2. Chứng minh MK cắt OH tại trung điểm.
3. Tính độ dài EF biết bán kính đường tròn tâm O là 1cm.
Bài 41:
Cho tam giác ABC, kéo dài AB thêm một đoạn BD = AC, kéo dài AC thêm một đoạn CE = AB, trung trực của BC cắt DE tại P. Chứng minh rằng: .
Bài 42:
Cho tam giác ABC cân tại A. Lấy D trên cạnh AC sao cho CD = 2AD. Lấy P trên đoạn thẳng BD sao cho góc APC = 900.
Chứng minh rằng: Ð ABP = Ð PCB.
Bài 43:
Cho tam giác đều BC. Một đường thẳng song song với AC cắt AB tại M và cắt BC tại P. Gọi D là tâm của tam giác đều BMP. E là trung điểm AP. Tính các góc của tam giác DEC.
Bài 44:
Cho tam giác ABC có góc B = 450, góc C = 300. Trên AC lấy điểm M sao cho góc MBC = 150. Chứng minh M là trung điểm AC.
Bài 45:
Cho tam giác ABC cân tại A. Qua A kẻ đường thẳng Ax song song BC. Lấy O trên Ax. Đường tròn tâm O tiếp xúc BC và cắt AB, AC tại D, E. Chứng minh tứ giác OADE nội tiếp.
Bài 46:
Cho tam giác ABM nội tiếp đường tròn tâm O có AB cố định và M di động. Hai đường cao BE và AF cắt nhau tại H. Lấy H làm tâm vẽ đường tròn tâm H bán kính HM cắt MB và MA lần lượt tại D và C.
1. Chứng minh B, D, C, A thuộc 1 đường tròn.
2. Chứng minh EF song song CD.