Ôn tập học kì II môn Vật lí lớp 8 - Phần III: Công - Công suất - định luật về công

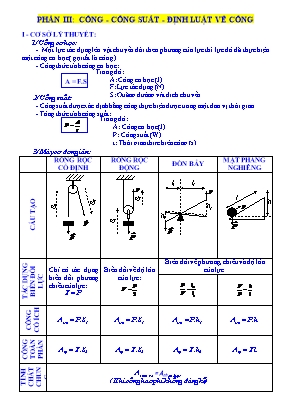
PHẦN III: CÔNG - CÔNG SUẤT - ĐỊNH LUẬT VỀ CÔNG
I - CƠ SỞ LÝ THUYẾT:
1/ Công cơ học:
- Một lực tác dụng lên vật chuyển dời theo phương của lực thì lực đó đã thực hiện một công cơ học ( gọi tắt là công).
Trong đó:
A: Công cơ học (J)
F: Lực tác dụng (N)
S: Quãng đường vật dich chuyển (m)
- Công thức tính công cơ học:
A = F.S
2/ Công suất:
- Công suất được xác định bằng công thực hiện được trong một đơn vị thời gian.
Trong đó:
A: Công cơ học (J)
P: Công suất (W)
t: Thời gian thực hiện công (s)
- Tông thức tính công suất:
3/ Máy cơ đơn giản:
RÒNG RỌC CỐ ĐỊNH
RÒNG RỌC ĐỘNG
ĐÒN BẢY
MẶT PHẲNG NGHIÊNG
CẤU TẠO
S2
S1
h1
S2
S1
l2
l1
h2
h
l
TÁC DỤNG
BIẾN ĐỔI LỰC
Chỉ có tác dụng biến đổi phương chiều của lực:
F = P
Biến đổi về độ lớn của lực:
Biến đổi về phương, chiều và độ lớn của lực.
CÔNG
CÓ ÍCH
Aich = P.S1
Aich = P.S1
Aich = P.h1
Aich = P.h
CÔNG TOÀN PHẦN
Atp = F.S2
Atp = F.S2
Atp = F.h2
Atp = Fl
TÍNH CHẤT CHUNG
Asinh ra = Anhận được
( Khi công hao phí không đáng kể)
HIỆU SUẤT
4/ Định luật về công:
Không một máy cơ đơn giản nào cho ta lợi về công. Được lợi bao nhiêu lần về lực thì thiệt bấy nhiêu lần về đường đi và ngược lại.
II/ BÀI TẬP ÁP DỤNG:
Bài 1: Một người kéo một gàu nước từ giếng sâu 10m. Công tối thiểu của người đó phải thực hiện là bao nhiêu? Biết gàu nước có khối lượnh là 1Kg và đựng thêm 5lít nước, khối lượng riêng của nước là 1000kg/m3.
Hướng dẫn giải:
Thể tích của nước: V = 5l = 0,005 m3
Khối lượng của nước: mn = V.D = 0,005 . 1000 = 5 (Kg)
Lực tối thiểu để kéo gàu nước lên là: F = P
Hay: F = 10(mn + mg) = 10(5 + 1) = 60(N)
Công tối thiểu của người đó phải thực hiện: A = F.S = 60. 10 = 600(J)
Bài 2: Người ta dùng một ròng rọc cố định để kéo một vật có khối lượng 10Kg lên cao 15m với lực kéo 120N.
a/ Tính công của lực kéo.
b/ Tính công hao phí để thắng lực cản.
Hướng dẫn giải:
a/ Công của lực kéo: A = F.S = 120.15 = 1800(J)
b/ Công có ích để kéo vật: Ai = P.S = 100.15 =1500(J)
Công hgao phí: Ahp = A - Ai = 1800- 1500 = 300 (J)
Bài 3: Để đưa một vật coa khối lượng 200Kg lên độ cao 10m người ta dùng một trong hai cách sau:
a/ Dùng hệ thống một ròng rọc cố định, một ròng rọc động. Lúc này lực kéo dây để nâng vật lên là F1 = 1200N.
Hãy tính:
- Hiệu suất của hệ thống.
- Khối lượng của ròng rọc động, Biết hao phí để nâng ròng rọc bằng hao phí tổng cộng do ma sát.
b/ Dùng mặt phẳng nghiêng dài l = 12m. Lực kéo lúc này là F2 = 1900N. Tính lực ma sát giữa vật và mặt phẳng nghiêng, hiệu suất của cơ hệ.
Hướng dẫn giải:
a/ Công dungd để nâng vật lên 10m:
A1 = 10.m.h = 20 000 (J)
- Khi dùng hệ thống ròng rọc trên thì khi vật lên cao một đoạn h thì phải kéo dây một đoạn S = 2h. Do đó công dùng để kéo vật:
A = F1 . S = F1 . 2h = 24000(J)
- Hiệu suất của hệ thống:
- Công hao phí: Ahp = A - A1 = 4000(J)
- Công hao phí để nâng ròng rọc động:
- Khối lượng của ròng rọc động: 
b/ Công có ích dùng để kéo vật là A1 = 20000(J)
- Công toàn phần kéo vật lúc nay:
A = F2. l = 22800(J)
- Công hao phí do ma sát: Ahp = A - A1 = 2800(J)
- Lực ma sát giữa vật và mặt phẳng nghiêng:
- Hiệu suất của mặt phẳng nghiêng:
Bài 4: Một đầu tàu kéo một toa tàu chuyển động từ ga A tới ga B trong 15phút với vận tốc 30Km/h. Tại ga B đoàn tàu được mắc thêm toa và do đó đoàn tàu đi từ ga B đến ga C với vận tốc nhỏ hơn 10Km/h. Thời gian đi từ ga B đến ga C là 30phút. Tính công của đầu tàu sinh ra biết rằng lực kéo của đầu tàu không đổi là 40000N.
Hướng dẫn giải:
- Quãng đường đi từ ga A đến ga B:
S1 = v1.t1 = 7,5 (Km) = 7500m
- Quãng đường đi từ ga B đến ga C:
S2 = v2.t2 = 10 (Km) = 10000m
- Công sinh ra: 
A = F (S1 + S2) = 700000000 (J) = 700000(KJ)
Bài 5: Người ta dùng một mặt phẳng ngiêng có chiều dài 3m để kéo một vật có khối lượng 300Kg với lực kéo 1200N . Hỏi vật có thể lên cao bao nhiêu? Biết hiệu suất của mặt phẳng nghiêng là 80%.
Hướng dẫn giải:
- Công của lự kéo vật:
A = F.l = 3600(J)
- Công có ích:
A1 = P.h = 10.m.h = 3000h (J)
- Độ cao vật có thể lên được:
Bài 6: 
Người ta dùng hệ thống ròng rọc để trục một vật cổ bằng đồng có trọng lượng
 P = 5340N từ đáy hồ sâu H = 10m lên (hình vẽ). Hãy tính:
Lực kéo khi:
Tượng ở phía trên mặt nước.
Tượng chìm hoàn toàn dưới nước.
Tính công tổng cộng của lực kéo tượng từ đáy hồ lên 
phía trên mặt nước h = 4m. Biết trọng lượng riêng của đồng và 
của nước lần lượt là 89000N/m3, 10000N/m3. Bỏ qua trọng lượng của các ròng rọc. 
Hướng dẫn giải:
1a/ Dùng ròng rọc động được lợi hai lần về lực, nên lực kéo khi vật đã lên khỏi mặt nước:
1b/ Khi vật còn ở dưới nước thì thể tích chiếm chỗ:
- Lực đẩy Acsimet tác dụng lên vật:
FA= V.d0 = 0,06.10000 = 600(N)
- Lực do dây treo tác dụng lên vật:
P1 = P - FA = 5340 - 600 = 4740 (N)
- Lực kéo vật khi còn trong nước:
2/ Do dùng ròng rọc động nên bị thiệt hai lần về đường đi nên công tổng cộng của lực kéo:
A =F1.2H + F. 2h = 68760 (J)
Bài 7: Người ta lăn 1 cái thùng theo một tấm ván nghiêng lên ôtô. Sàn xe ôtô cao 1,2m, ván dài 3m. Thùng có khối lượng 100Kg và lực đẩy thùng là 420N.
a/ Tình lực ma sát giữa tấm ván và thùng.
b/ Tình hiệu suất của mặt phẳng nghiêng.
Hướng dẫn giải: 
- Nếu không có ma sát thì lực đẩy thùng là:
- Thực tế phải đẩy thùng với 1 lực 420N vậy lực ma sát giữa ván và thùng:
Fms = F - F' = 20(N)
- Công có ích để đưa vật lên:
Ai = P . h = 1200(J)
- Công toàn phần để đưa vật lên:
A = F. S = 1260 (J)
- Hiệu suất mặt phẳng nghiêng:
Bài 8: Người ta dùng một palăng để đưa một kiện hàng lên cao 3m. Biết quãng đường dịch chuyển của lực kéo là 12m.
a/ Cho biết cấu tạo của palăng nói trên.
b/ Biết lực kéo có giá trị F = 156,25N. Tính khối lượng của kiện hàng nói trên.
c/ Tính công của lực kéo và công nâng vật không qua palăng. Từ đó rút ra kết luận gì?
Hướng dẫn giải:
a/ Số cặp ròng rọc: 
(Cặp)
Vậy palăng được cấu tạo bởi 2 ròng rọc cố định và 2 ròng rọc động.
b/ Ta có: 
- Trọng lượng của kiện hàng:
P = 4F = 4. 156,25 = 625(N)
- Khối lượng của kiện hàng:
c/ công của lực kéo:
Ak = FK.S' = 156,25.12 = 1875 (J)
- Công của lực nâng vật:
An = P.S = 625.3 = 1875(J)
- Hệ thống palăng không cho lợi về công.
Bài 9: Cho hệ giống như hình vẽ. vật m1 có khối lượng 10Kg, vật m2 có khối lượng 6Kg. Cho khoảng cách AB = 20cm. Tính chiều dài của thanh OB để hệ cân bằng. 
F'
A
O
B
m2
m1
P2 = F2
P1 = F1
Hướng dẫn giải:
- Trọng lượng của vật m1:
P1 = F1 = 10.m1 = 100N
- Trọng lượng của vật m2:
P2 = F2 = 10.m2 = 60N
- Do vật m1 nặng hơn m2 nên m1 đi xuống vậy đầu B có xu thế đi lên:
- Độ lớn lực tác dụng lên đầu B
- Áp dụng hệ thức cân bằng của đòn bảy ta có:
- Chiều dài thanh OB:
OB = OA + AB = 100 + 20 = 120 (cm)
Bài 10: Thanh AB dài 160cm, ở đầu A người ta treo một vật có khối lượng m1 = 9Kg, điểm tựa O nằm cách A một đoạn 40cm.
a/ Hỏi phải treo vào đầu b một vật m2 có khối lượng bao nhiêu để thanh cân bằng?
b/ Vật m2 giữ nguyên không đổi, bay giờ người ta dịch chuyển điểm O về phía đầu B và cách B một đoạn 60cm. Hỏi vật m1 phải thay đổi như thế nào để thanh vẫn ccân bằng?
Hướng dẫn giải:
a/ Ta có: OA = 40cm
Trọng lượng của vật m1:
P1 = F1 = 10.m1 = 90N
Áp dụng hệ thức cân bằng của đòn bảy:
Lực tác dụng vào đầu B:
Vậy để thanh AB cân bằng thì phải treo vào đầu B vật m2 = 3Kg.
b/ Ta có: OB = 60cm
Áp dụng hệ thức cân bằng của đòn bảy, để thanh AB cân bằng thì lực tác dụng vào đầu A:
Vậy vật m1 = 1,8Kg tức là vật m1 phải bớt đi 7,2Kg.
III/ BÀI TẬP TỰ GIẢI:
Bài 1: Một khối gỗ hình hộp chữ nhật có diện tích đáy là S = 150 cm2 cao h = 30cm, khối gỗ được thả nổi trong hồ nước sâu H = 0,8m sao cho khối gỗ thẳng đứng. Biết trọng lượng riêng của gỗ bằng 2/3 trọng lượng riêng của nước và = 10 000 N/m3. 
 Bỏ qua sự thay đổi mực nước của hồ, hãy :
a) Tính chiều cao phần chìm trong nước của khối gỗ ? 
b) Tính công của lực để nhấc khối gỗ ra khỏi nước H
 theo phương thẳng đứng ? 
c) Tính công của lực để nhấn chìm khối gỗ đến đáy
 hồ theo phương thẳng đứng ?
Bài 2: Dùng một mặt phẳng nghiêng để kéo một vật có khối lượng 200kg,trọng lượng riêng d=8800(N/m3) lên cao 4m với vận tốc 0,2m/s ,trong thời gian 1phút 40giây.Hiệu suất của mặt phẳng nghiêng 80%.
 a/Tính trọng lượng và thể tích của vật.
 b/Tính chiều dài và lực kéo trên mặt phẳng nghiêng. 
 c/Tính công suất nâng vật. 
Bài 3: Dùng mặt phẳng nghiêng đẩy một bao xi măng có khối lượng 50Kg lên sàn ô tô . Sàn ô tô cách mặt đất 1,2 m.
a/Tính chiều dài của mặt phẳng nghiêng sao cho người công nhân chỉ cần tạo lực đẩy bằng 200N để đưa bì xi măng lên ô tô . Giả sử ma sát giữa mặt phẳng nghiêng và bao xi măng không đáng kể .
b/ Nhưng thực tế không thêt bỏ qua ma sát nên hiệu suất của mặtphẳng nghiêng là 75% . Tính lực ma sát tác dụng vào bao xi măng.
Bài 4: Một thang máy có khối lượng m = 580kg, được kéo từ đáy hầm mỏ sâu 125m lên mặt đất bằng lực căng của một dây cáp do máy thực hiện.
	a) Tính công nhỏ nhất của lực căng để thực hiện việc đó.
	b) Biết hiệu suất của máy là 75%. Tính công do máy thực hiện và công hao phí do lục cản.
Bài 5: Người ta kéo một vật A, có khối lượng mA = 10g, chuyển động đều lên mặt phẳng nghiêng (như hình vẽ).
C
D
E
A
B
Biết CD = 4m; DE = 1m.
a/ Nếu bỏ qua ma sát thì vật B phải 
có khối lượng mB là bao nhiêu?
b/ Thực tế có ma sát nên để kéo vật
A đi lên đều người ta phải treovật B
có khối lượng m’B = 3kg. Tính hiệu 
suất của mặt phẳng nghiêng. Biết dây
nối có khối lượng không đáng kể.
Bài 6: Từ dưới đất kéo vật nặng lên cao người ta mắc một hệ thống gồm ròng rọc động và ròng rọc cố định. Vẽ hình mô tả cách mắc để được lợi:
a/ 2 lần về lực.
b/ 3 lần về lực.
Muốn đạt được điều đó ta phải chú ý đến những điều kiện gì?
Bài 7: Cho 1 hệ như hình vẽ ,thanh AB có khối lượng không đáng kể , ở hai đầu có treo hai quả cầu bằng nhôm có trọng lượng PA và PB.Thanh được treo nằm ngang bằng một sợi dây tại điểm O hơi lệch về phía A . Nếu nhúng hai quả cầu này vào nước thì thanh còn cân bằng nữa không? tại sao?
O
PB
PA
B
A
Bài 8: Người ta dùng một cái xà beng có dạng như hình vẽ (Hình2) để nhổ một cây đinh cắm sâu vào gỗ. 
a/ Khi tác dụng một lực F =100N vuông góc với OB tại đầu B ta sẽ nhổ được đinh. Tính lực giữ của đinh lúc này? Biết OB= 10.OA.(Có biểu diễn lực trong hình vẽ)
b/ Nếu lực tác dụng vào đầu B có hướng vuông góc với tấm gỗ thì phải có độ lớn là bao nhiêu mới nhổ được đinh.(Có biểu diễn lực trong hình vẽ).
Bài 9: Ô tô có khối lượng 1200 kg khi chạy trên đường nằm ngang với vận tốc V= 72 km/h thì tiêu hao 80g xăng trên đoạn đờng S = 1 km. Hiệu suất động cơ là 20%.
a/ Tính công suất của ô tô.
b/ Hỏi với những điều kiện như vậy thì ô tô đạt vận tốc bao nhiêu khi nó leo dốc ? Biết rằng cứ mỗi quãng đường l = 100m thì đọ cao tăng thêm h = 2 cm. Cho biết năng suất toả nhiệt của xăng là q = 45.106 J/kg.
Bài 10: Cho một hệ thống như hình vẽ.
Hai vật A và B đứng yên. Ma sát không đáng kể. Vật A và vật B có nặng bằng nhau không ?
Cho MN = 80 cm, NH = 5 cm. Tính tỷ số khối lượng của hai vật A và B
 N
 A
 B
 H M
Bài 11: Tính lực kéo F trong các trường hợp sau đây. Biết vật nặng có trọng lượng P = 120 N (Bỏ qua ma sát, khối lượng của các ròng rọc và dây ).
F
F
F
F
F
F
P
·
·
·
·
·
4F
F
F
F
2F
2F
4F
P
·
·
·
·
F
F
F
F
F
F
F
P
·
·
·
·
·
·
Bài 12: Trong bình đựng hai chất lỏng không trộn lẫn có trọng lượng riêng d1=12000N/m3; d2=8000N/m3. Một khối gỗ hình lập phương cạnh a = 20cm có trọng lượng riêng d = 9000N/m3được thả vào chất lỏng.
a/ Tìm chiều cao của phần khối gỗ trong chất lỏng d1?
	 b/ Tính công để nhấn chìm khối gỗ hoàn toàn trong chất lỏng d1? Bỏ qua sự thay đổi mực nước.
Bài 13:Ô tô có khối lượng 1200 kg khi chạy trên đường nằm ngang với vận tốc V= 72 km/h thì tiêu hao 80g xăng trên đoạn đường S = 1 km. Hiệu suất động cơ là 20%.
a/ Tính công suất của ô tô.
b/ Hỏi với những điều kiện như vậy thì ô tô đạt vận tốc bao nhiêu khi nó leo dốc ? Biết rằng cứ mỗi quãng đường l = 100m thì độ cao tăng thêm h = 2 cm. Cho biết năng suất toả nhiệt của xăng là q = 45.106 J/kg.
A
Bài 14: Vật A ở hình bên có khối lượng 2kg. Hỏi lực kế chỉ bao nhiêu ?
 Muốn vật A đi lên được 2cm, ta phải kéo lực kế đi xuống bao nhiêu cm ?
Bài 15: Một xe cút kít chở một vật nặng 1500N. Khi người công nhân đẩy cho xe chuyển động đều phương của trọng lượng cắt mặt xe ở một điểm cách trục bánh xe 80cm.
a/ Tìm lực tác dụng thẳng đứng của mỗi tay vào càng xe, biết rằng mỗi tay cách càng xe một đoạn là 1,6m.
b/ Tìm lực đè của bánh xe lên mặt đường.
Bài 16: Công suất trung bình của động cơ kéo tời là 73,5W và hiệu suất của tời là 0,9. Hãy tính:
a/ Độ cao mà động cơ kéo vật nặng 588N lên được trong một phút.
b/ Số vòng quay của tời trong một phút. Biết bán kính của tời là 5cm.
c/ Độ lớn của lực tác dụng vuông góc vào tay quay, cho biết chiều dài tay quay là 30cm.
Bài 17: Một bể nước hình trụ thẳng đứng cao 3m đường kính 0,7m. Người ta bơm nước cho đầy bể từ một mực nước thấp hơn đáy bể 8m.
a/ Tính công thực hiệnđể bơm nước đầy bbẻ vaói giả thiết ma sát giữa nước và ống dẫn không đáng kể.
b/ Tính công suất máy bơm biết rằng cần 20phút để bơm đầy bể.
Bài 18: Một trục kéo với tay quay dài 60cm và hình tru có bán kính 15cm, được dùng để lấy nướcở một giếng sau 10m. Thùng chứa nước có dung tích 10lít.
a/ Tính lực tác dụng vào tay quay khi kéo một thùng nước lên.
b/ Tính công cần dùng để kéo 100lít nước lên.
c/ Tính quãng đường đi của đầu tay quay và số vòng quay khi kéo lên được một thùng nước.
d/ Tính công suất trung binh khi kéo được 100lit mỗi giờ.
Bài 19: Một xe lữa có răng cưa đi trên một đoạn đường dốc dài 5Km. Khoảng cách thẳng đứng giữa hai điểm đầu của dốc là 1,5Km. mỗi toa xe kể cả hành khách nặng 5tấn.
a/ Tính lực kéo của động cơ để lôi một toa xe lên theo đường dốc.
b/ Tính công cần dùng để kéo toa xe lên.
c/ Xe lữa lên dốc với vận tốc trung bình là 12Km/h. Tính công suất của động cơ dùng để kéo hai toa xe lên.
d/ Dùng năng lượng một thác nước cao 10m. Biết công hao phí là 25% công phát động. Tính lượng nước cần dùng mỗi giờ để làm chuyển vận động cơ kéo hai toa xe lên.
Bài 20: Một người đi xe đạp có khối lượng cả người lẫn xe là 80Kg chuyển động trên một đường bằng với vận tốc 18Km/h. Các lực ma sát nghịch chiều với chuyển động là 7N và lực cản của không khí là 5N. tính:
a/ Công tạo nên bởi người xe đạp khi đi 1Km trên đường bằng.
b/ công suất của người xe đạp trong điều kiện ở câu a.
c/ Công suất của người xe đạp trong trường hợp người này phải chuyển động trên một đường dốc nhưng muốn giữ vận tốc trên đường bằng. Dốc là đốc cao 2m lúc đường đi dài 100m.
Bài 21: Công đưa một vật lên cao 4m bằng mặt phẳng nghiêng là 6000J.
a/ Tính trọng lượng của vật. Biết mặt phẳng nghiêng có hiệu suất 80%.
b/ Tính công để thắng lực ma sát khi kéo vật lên và xác định lực ma sát đó, biết mặt phẳng nghiêng có chiều dài l = 20m.
c/ Để đưa vật lại xuống đất phải tác dụng vào vật một lực như thế nào? Tính độ lớn của lực đó.
PHẦN IV: ÁP SUẤT - ÁP SUẤT CHẤT LỎNG - ÁP SUẤT KHÍ QUYỂN - LỰC ĐẨY AC-SI-MET
I - CƠ SỞ LÝ THUYẾT:
1/ Áp suất:
- Công thức tính áp suất: 	
- Đơn vị áp suất là paxcan(Pa): 
2/ Áp suất chất lỏng:
- Chất lỏng đựng trong bình sẽ gây áp suất theo mọi phương lên đáy bình, thành bình và mọi vật đặt trong nó.
- Công thức tính áp suất chất lỏng: P = d.h	( Với d là trọng lượng riêng của chất lỏng; h là chiều cao (độ sâu) của cột chất lỏng tính từ mặt thoáng chất lỏng)
Chú ý: 
Trong cột chất lỏng đứng yên, áp suất của mọi điểm trên cùng mặt phẳng nằm ngang có độ lớn như nhau (cùng độ sâu)
Một vật nằm trong lòng chất lỏng, thì ngoài áp suất chất lỏng, vật còn chịu thêm áp suất khí quyển do chất lỏng truyền tới.
3/ Bình thông nhau:
- Trong bình thông nhau chứa cùng chất lỏng đứng yên, các mặt thoáng của chất lỏng ở các nhánh khác nhau đều ở một độ cao.
- Trong bình thông nhau chứa hai hay nhiều chất lỏng không hòa tan, thì mực mặt thoáng không bằng nhau, trong trường hợp này áp suất tại mọi điểm trên cùng mặt phẳng nằm ngang có giá trị bằng nhau.
- Bài toán máy dùng chất lỏng: Áp suất tác dụng lên chất lỏng được chất lỏng truyền đi nguyên vẹn theo mọi hướng.
+ Xác định độ lớn của lực: Xác định diện tích của pittông lớn, pittông nhỏ.
+ Đổi đơn vị thích hợp.
4/ Áp suất khí quyển:
- Do không khí có trọng lượng nên Trái Đất và mọi vật trên Trái Đất chịu tác dụng của áp suất khí quyển. Giống như áp suất chất lỏng áp suất này tác dụng theo mọi phương.
- Áp suất khí quyển được xác định bằng áp suất cột thủy ngân trong ống Tô-ri-xe-li.
- Đơn vị của áp suất khí quyển là mmHg (760mmHg = 1,03.105Pa)
- Càng lên cao áp suất khí quyển càng giảm ( cứ lên cao 12m thì giảm 1mmHg).
5/ Lực đẩy Acsimet:
- Mọi vật nhúng trong chất lỏng đều bị chất lỏng đẩy thẳng đứng từ dưới lên với một lực có độ lớn bằng trọng lượng của phần chất lỏng mà vật chiếm chỗ. Lực này được gọi là lực đẩy Acsimet.
- Công thức tính: FA = d.V
- Điều kiện vật nổi, chìm, lơ lửng: 
+ FA > P Vật nổi
+ FA = P Vật lơ lửng
+ FA < P Vật chìm
Phần IV: NHIỆT HỌC
I - CƠ SỞ LÝ THUYẾT:
1/ Nguyên lý truyền nhiệt: 
Nếu chỉ có hai vật trao đổi nhiệt thì:
- Nhiệt tự truyền từ vật có nhiệt độ cao hơn sang vật có nhiệt độ thấp hơn.
- Sự truyền nhiệt xảy ra cho đến khi nhiệt độ của hai vật bằng nhau thì dừng lại.
-Nhiệt lượng của vật này tỏa ra bằng nhiệt lượng của vật khi thu vào.
2/ Công thức nhiệt lượng:
- Nhiệt lượng của một vật thu vào để nóng lên: Q = mc∆t (với ∆t = t2 - t1. Nhiệt độ cuối trừ nhiệt độ đầu)
- Nhiệt lượng của một vật tỏa ra để lạnh đi: Q = mc∆t (với ∆t = t1 - t2. Nhiệt độ đầu trừ nhiệt độ cuối)
- Nhiệt lượng tỏa ra và thu của các chất khi chuyển thể:
	+ Sự nóng chảy - Đông đặc: Q = mλ (λ là nhiệt nóng chảy)
	+ Sự hóa hơi - Ngưng tụ: Q = mL (L là nhiệt hóa hơi)
- Nhiệt lượng tỏa ra khi nhiên liệu bị đốt cháy: 
	Q = mq (q năng suất tỏa nhiệt của nhiên liệu)
- Nhiệt lượng tỏa ra trên dây dẫn khi có dòng điện chạy qua: 
Q = I2Rt
3/ Phương trình cân bằng nhiệt: 
Qtỏa ra = Qthu vào
4/ Hiệu suất của động cơ nhiệt: 
H = 
5/ Một số biểu thức liên quan:
- Khối lượng riêng: D = 
- Trọng lượng riêng: d = 
- Biểu thức liên hệ giữa khối lượng và trọng lượng: P = 10m
- Biểu thức liên hệ giữa khối lượng riêng và trọng lượng riêng: d = 10D
II - BÀI TẬP VẬN DỤNG
Bài 1: Người ta thả một thỏi đồng 0,4kg ở nhiệt độ 800C vào 0,25kg nước ở nhiệt độ 180C. Hãy xác định nhiệt độ khi cân bằng nhiệt. Cho biết nhiệt dung riêng của đồng là 380J/kg.k của nước là 4200J/Kg.K.
Hướng dẫn giải:
- Nhiệt lượng do miếng đồng tỏa ra để nguội đi từ 800C xuống t0C:
Q1 = m1.C1.(t1 - t) = 0,4. 380. (80 - t) (J)
- Nhiệt lượng nước thu vào để nóng lên từ 180C đến t0C:
Q2 = m2.C2.(t - t2) = 0,25. 4200. (t - 18) (J)
Theo phương trình cân bằng nhiệt: 
Q1 = Q2
0,4. 380. (80 - t) = 0,25. 4200. (t - 18)
t ≈ 260C
Vậy nhiệt độ xảy ra cân bằng là 260C.
Bài 2: Trộn lẫn rượu và nước người ta thu được hỗn hợp nặng 140g ở nhiệt độ 360C. Tính khối lượng của nước và khối lượng của rượu đã trộn. Biết rằng ban đầu rượu có nhiệt độ 190C và nước có nhiệt độ 1000C, cho biết nhiệt dung riêng của nước là 4200J/Kg.K, của rượu là 2500J/Kg.k.
Hướng dẫn giải:
- Theo bài ra ta biết tổng khối lượng của nước và rượu là 140
m1 + m2 = m m1 = m - m2 (1)
- Nhiệt lượng do nước tỏa ra: Q1 = m1. C1 (t1 - t)
- Nhiệt lượng rượu thu vào: Q2 = m2. C2 (t - t2)
- Theo PTCB nhiệt: Q1 = Q2
m1. C1 (t1 - t) = m2. C2 (t - t2)
m14200(100 - 36) = m22500 (36 - 19)
268800 m1 = 42500 m2
 (2)
- Thay (1) vào (2) ta được:
268800 (m - m2) = 42500 m2
37632 - 268800 m2 = 42500 m2
311300 m2 = 37632
m2 = 0,12 (Kg)
- Thay m2 vào pt (1) ta được:
(1) m1 = 0,14 - 0,12 = 0,02 (Kg)
Vậy ta phải pha trộn là 0,02Kg nước vào 0,12Kg. rượu để thu được hỗn hợp nặng 0,14Kg ở 360C.
Bài 3: Người ta đổ m1(Kg) nước ở nhiệt độ 600C vào m2(Kg) nước đá ở nhiệt độ -50C. Khi có cân bằng nhiệt lượng nước thu được là 50Kg và có nhiệt độ là 250C . Tính khối lượng của nước đá và nước ban đầu. Cho nhiệt dung riêng của nước đá là 2100J/Kg.k. (Giải tương tự bài số 2)
Bài 4: Người ta dẫn 0,2 Kg hơi nước ở nhiệt độ 1000C vào một bình chứa 1,5 Kg nước đang ở nhiệt độ 150C. Tính nhiệt độ cuối cùng của hỗn hợp và tổng khối lượng khi xảy ra cân bằng nhiệt.
Hướng dẫn giải: 
Nhiệt lượng tỏa ra khi 0,2 Kg hơi nước ở 1000C ngưng tụ thành nước ở 1000C
Q1 = m1. L = 0,2 . 2,3.106 = 460000 (J)
Nhiệt lượng tỏa ra khi 0,2Kg nước ở 1000C thành nước ở t0C
Q2 = m1.C. (t1 - t) = 0,2. 4200 (100 - t)
Nhiệt lượng thu vào khi 1,5Kg nước ở 150C thành nước ở t0C
Q3 = m2.C. (t - t2) = 1,5. 4200 (t - 15)
Áp dụng phương trình cân bằng nhiệt:
Q1 + Q2 = Q3
460000 + 0,2. 4200 (100 - t) = 1,5. 4200 (t - 15)
6780t = 638500
t ≈ 940C
Tổng khối lượng khi xảy ra cân bằng nhiệt.
m = m1 + m2 = 0,2 + 1,5 = 1,7(Kg)
Bài 5: Có ba chất lỏng không tác dụng hóa học với nhau và được trộn lẫn vào nhau trong một nhiệt lượng kế. chúng có khối lượng lần lượt là m1=1kg, m2= 10kg, m3=5kg, có nhiệt dung riêng lần lượt là C1 = 2000J/Kg.K, C2 = 4000J/Kg.K, C3 = 2000J/Kg.K và có nhiệt độ là t1 = 60C, t2 = -400C, t3 = 600C.
a/ Hãy xác định nhiệt độ của hỗn hợp khi xãy ra cân bằng.
b/ Tính nhiệt lượng cần thiết để hỗn hợp được nóng lên thêm 60C. Biết rằng khi trao đổi nhiệt không có chất nào bị hóa hơi hay đông đặc.
Hướng dẫn giải:
a/ Giả sử rằng, thoạt đầu ta trộn hai chất có nhiệt độ thấp hơn với nhau ta thu được một hỗn hợp ở nhiệt độ t < t3 ta có pt cân bằng nhiệt:
m1C1(t1 - t) = m2C2(t - t2)
	(1)
Sau đó ta đem hỗn hgợp trên trôn với chất thứ 3 ta thu được hỗn hợp 3 chất ở nhiệt độ t' (t < t' < t3) ta có phương trình cân bằng nhiệt:
(m1C1 + m2C2)(t' - t) = m3C3(t3 - t')	(2)
Từ (1) và (2) ta có:
Thay số vào ta tính được t' ≈ -190C
b/ Nhiệt lượng cần thiết để nâng nhiệt độ của hỗn hợp lên 60C:
Q = (m1C1 + m2C2 + m3C3) (t4 - t') = 1300000(J)
Bài 6: Một thỏi nước đá có khối lượng 200g ở -100C.
a/ Tính nhiệt lượng cần cung cấp để nước đá biến thành hơi hoàn toàn ở 1000C.
b/ Nếu bỏ thỏi nước đá trên vào một xô nước bằng nhôm ở 200C. Sau khi cân bằng nhiệt ta thấy trong xô còn lại một cục nước đá coa khối lượng 50g. tính lượng nước đã có trong xô lúc đầu. Biết xô có khối lượng 100g.
Hướng dẫn giải:
a/ Nhiệt lượng nước đá thu vào để tăng nhiệt độ từ -100C đến 00C
Q1 = m1C1(t2 - t1) = 3600(J)
Nhiệt lượng nước đá thu vào để nóng chảy hoàn toàn ở 00C
Q2 = m1.λ = 68000 (J)
Nhiệt lượng nước thu vào để tăng nhiệt độ từ 00C đến 1000C
Q3 = m3C2(t3 - t2) = 84000(J)
Nhiệt lượng nước thu vào để hóa hơi hoàn toàn ở 1000C
Q4 = m1.L = 460000(J)
Nhiệt lượng cần cung cấp trong suốt quá trình:
Q = Q1 + Q2 + Q3 + Q4 = 615600(J)
b/ Gọi m' là lượng nước đá đã tan: m' = 200 - 50 = 150g = 0,15Kg
Do nước đá tan không hết nên nhiệt độ cuối cùng của hỗn hợp là 00C. 
Nhiệt lượng mà m' (Kg) nước đá thu vào để nóng chảy:
Q' = m'λ = 51000 (J)
Nhiệt lượng do m'' Kg nước và xô nhôm tỏa ra để giảm xuống từ 200C đến 00C
Q" = (m"C2 + mnhCnh)(20 - 0)
Áp dụng phương trình cân bằng nhiệt:
Q" = Q' + Q1 hay:
(m"C2 + mnhCnh)(20 - 0) = 51000 + 3600
m" = 0,629 (Kg)
Bài 7: Khi thực hành trong phòng thí nghiệm, một học sinh cho một luồng hơi nước ở 1000C ngưng tụ trong một nhiệt lượng kếchứa 0,35kg nước ở 100C. Kết quả là nhiệt độ của nước tăng lên 420C và khối lượng nước trong nhhiệt kế tăng thêm 0,020kg. Hãy tính nhiệt hóa hơi của nước trong thí nghiệm này?
Hướng dẫn giải:
Nhiệt lượng mà 0,35kg nước thu vào:
Q Thu vào = m.C.(t2 - t1) ≈ 46900(J)
Nhiệt lượng mà 0,020Kg hơi nước ở 1000C ngưng tụ thành nước
Q1 = m.L = 0,020L
Nhiệt lượng mà 0,020Kg nước ở 1000C tỏa ra khi hạ xuống còn 420C
Q 2 = m'.C.(t3 - t2) ≈ 4860(J)
Theo phương trình cân bằng nhiệt:
Q Thu vào = Q1 + Q 2 hay:
46900 = 0,020L + 4860
L = 21.105 (J/Kg)
Bài 8: Có hai bình cách nhiệt, bình thứ nhất chứa 2Kg nước ở 200C, bình thứ hai chứa 4Kg nước ở 600C. Người ta rót một ca nước từ bình 1 vào bình 2. Khi bình 2 đã cân bằng nhiệt thì người ta lại rót một ca nước từ bình 2 sang bình 1 để lượng nước trong hai bình như lúc đầu. Nhiệt độ ở bình 1 sau khi cân bằng là 21,950C. 
a/ Xác định lượng nước đã rót ở mỗi lần và nhiệt độ cân bằng ở bình 2.
b/ Nếu tiếp tục thực hiện lần thứ hai, tìm nhiệt độ cân bằng ở mỗi bình.
Hướng dẫn giải:
a/ Giả sử khi rót lượng nước m từ bình 1 sang bình 2, nhiệt độ cân bằng của bình 2 là t nên ta có phương trình cân bằng:
m.(t - t1) = m2.(t2 - t) 	(1)
Tương tự lần rót tiếp theo nhiệt độ cân bằng ở bình 1 là t' = 21,950C và lượng nước trong bình 1 lúc này chỉ còn (m1 - m) nên ta có phương trình cân bằng:
m.(t - t') = (m1 - m).(t' - t1) 	(2)
Từ (1) và (2) ta có pt sau:
m2.(t2 - t) = m1.(t' - t1)
	(3)
Thay (3) vào (2) tính toán ta rút phương trình sau:
	(4)
Thay số vào (3) và (4) ta tìm được: t = 590C và m = 0,1 Kg.
b/ Lúc này nhiệt độ của bình 1 và bình 2 lần lượt là 21,950C và 590C bây giờ ta thực hiện rót 0,1Kg nước từ bình 1 sang bình 2 thì ta có thể viết được phương trình sau:
m.(T2 - t') = m2.(t - T2)
Bây giờ ta tiếp tục rơt từ bình 2 sang bình 1 ta cũng dễ dàng viết được phương trình sau:
m.(T1 - T2) = (m1 - m).(t - T1)
Bài 9: Bếp điện có ghi 220V-800W được nối với hiệu điện thế 220V được dùng để đun sôi 2lít nước ở 200C. Biết hiệu suất của bếp H = 80% và nhiệt dung riêng của nước là 4200J/kg.K.
a/ Tính thời gian đun sôi nước và điện năng tiêu thụ của bếp ra Kwh.
b/ Biết cuộn dây có đường kính d = 0,2mm, điện trở suất được quấn trên một lõi bằng sứ cách điện hình trụ tròn có đường kính D = 2cm. Tính số vòng dây của bếp điện trên.
Hướng dẫn giải:
a/ Gọi Q là nhiệt lượng mà nước thu vào để nóng lên từ 200C đến 1000:
Q = m.C.∆t
Gọi Q' là nhiệt lượng do dòng điện tỏa ra trên dây đốt nóng
Q' = R.I2.t = P. t
Theo bài ra ta có: 
Điện năng tiêu thụ của bếp:
A = P. t = 233,33 (Wh) = 0,233 (Kwh)
b/ Điện trở của dây: 
 (1)
Mặt khác: (2)
Từ (1) và (2) ta có:
Bài 10: Cầu chì trong mạch điện có tiết diện S = 0,1mm2, ở nhiệt độ 270C. Biết rằng khi đoản mạch thì cường độ dòng điện qua dây chì là I = 10A. Hỏi sau bao lâu thì dây chì đứt? Bỏ qua sụ tỏa nhiệt ra môi trường xung quanh và sự thay đổi điện trở, kích thước dây chì theo nhiệt độ. cho biết nhiệt dung riêng, điện trỏe suất, khối lượng riêng, nhiệt nóng chảy và nhiệt độ nóng chảy của chì lần lượt là: C = 120J/kg.K; ; D = 11300kg/m3; ; tc=3270C.
Hướng dẫn giải:
Gọi Q là nhiệt lượng do dòng điện I tỏa ra trong thời gian t, ta có:
Q = R.I2.t = ( Với l là chiều dài dây chì)
Gọi Q' là nhiệt lượng do dây chì thu vào để tăng nhiệt độ từ 270C đến nhiệt độ nóng chảy tc = 3270C và nóng chảy hoàn toàn ở nhiệt độ nóng chảy, ta có
Q' = m.C.∆t + mλ = m(C.∆t + λ) = DlS(C.∆t + λ) với (m = D.V = DlS)
 Do không có sự mất mát nhiệt nên:
Q = Q' hay: = DlS(C.∆t + λ)
III - BÀI TẬP TỰ GIẢI
Bài 1: Một nhiệt lượng kế bằng đồng có khối lượng 200g đựng 1,6 Kg nước ở 800C, người ta thả 1,6Kg nước đá ở -100C vào nhiệt lượng kế.
a/ Nước đá có tan hết không?
b/ Nhiệt độ cuối cùng của nhiệt lượng kế là bao nhiêu? Cho biết nhiệt dung riêng của đồng 380J/kg.K; của nước đá là 2100J/kg.K; của nước là 4190J/kg.K; Nhiệt nóng chảy của nước đá là 336.103 J/Kg.
Bài 2: Phải trộn bao nhiêu nước ở nhiệt độ 800C vào nước ở 200C để được 90Kg nước ở 600C. Cho biết nhiệt dung riêng của nước là 4200/kg.K.
Bài 3: Người ta bỏ một cục nước đá có khối lượng 100g vào một nhiệt lượng kế bằng đồng có khối lượng 125g, thì nhiệt độ của nhiệt lượng kế và nước đá là -200C. Hỏi cần phải thêm vào nhiệt lượng kế bao nhiêu nước ở 200C để làm tan được một nửa lượng nước đá trên? Cho biết nhiệt dung riêng của đồng 380J/kg.K; của nước đá là 2100J/kg.K; của nước là 4200J/kg.K; Nhiệt nóng chảy của nước đá là 3,4.105 J/Kg.
Bài 4: Có hai bình cách nhiệt, bình thứ nhất chứa 4lít nước ở 800C, bình thứ hai chứa 2lít nước ở 200C. Người ta rót một ca nước từ bình 1 vào bình 2. Khi bình 2 đã cân bằng nhiệt thì người ta lại rót một ca nước từ bình 2 sang bình 1 để lượng nước trong hai bình như lúc đầu. Nhiệt độ ở bình 1 sau khi cân bằng là 740C. Xác định lượng nước đã rót ở mỗi lần.
Bài 5: Có hai bình cách nhiệt, bình A chứa 4kg nước ở 200C, bình B chứa 8kg nước ở 400C. Người ta rót một lượng nước có khối lượng m từ bình B sang bình A. Khi bình A đã cân bằng nhiệt thì người ta lại rót một lượng nước như lúc đầu từ bình A sang bình B. Nhiệt độ ở bình B sau khi cân bằng là 380C. Xác định lượng nước m đã rót và nhiệt độ cân bằng ở bình A.
Bài 6: Bỏ 25g nước đá ở 00C vào một cái cốc chứa 0,5kg nước ở 400C. Hỏi nhiệt độ cuối cùng của cốc là bao nhiêu? Biết nhiệt dung riêng của nước là C = 4190J/Kg.K; Nhiệt nóng chảy của nước đá là 
Bài 7: Trộn lẫn ba phần nước có khối lượng lần lượt là m1 = 50kg, m2 = 30kg, m3 = 20kg. có nhiệt độ lần lượt là t1 = 600C, t2 = 400C, t3 = 200C; Cho rằng m1 truyền nhiệt cho m2 và m3. Bỏ qua sự mất mát nhiệt, tín nhiệt độ của hỗn hợp. Biết nhiệt dung riêng của nước là 4200J/Kg.K. ( Giải tương tự bài số 5)
Bài 8: Một phích nước nóng có nhiệt độ không đổi, một cái cốc và một nhiệt kế. Ban đầu cốc và nhiệt kế có nhiệt độ t = 250C. Người ta rót nước từ phích vào đầy cốc và thả nhiệt kế vào cốc, nhiệt kế chỉ t1 = 600C. Đổ nước cũ đi thì nhiệt độ của cốc và nhiệt kế là t' = 550C, lại rót từ phích vào đầy cốc, nhiệt kế chỉ t2 = 750C. Cho rằng thời gian từ lúc rót nước vào cốc đến lúc đọc nhiệt độ là rất nhỏ. Cho nhiệt dung riêng của nước là C, của cốc và nhiệt kế là C1. hỏi nhiệt độ của nước trong phích là bao nhiêu?
Bài 9: Rót nước ở nhiệt độ 200C vào một nhiệt lượng kế. Thả trong nước một cục nước đá có khối lượng 0,5kg và ở nhiệt độ -150C. Hãy tính nhiệt độ của hỗn hợp sau khi cân bằng nhiệt. Biết khối lượng của nước rót vào bằng khối lượng của nước đá.
Bài 10: Để xác định nhiệt hóa hơi của nước người ta thực hiện thí nghiệm như sau:
Lấy 0,02kg hơi nước ở 1000C cho ngưng tụ trong ống nhiệt lượng kế chứa 0,35kg nước ở 100C. Nhiệt độ cuối cùng đo được là 420C. Hãy dựa vào các số liệu trên tính lại nhiệt hóa hơi của nước. 
Bài 11: Người ta bỏ một cục sắt khối lượng m1 = 100g có nhiệt độ t1 = 5270C vào một bình chứa m2 = 1kg nước ở nhiệt độ t2 = 200C. Hỏi đã có bao nhiêu gam nước kịp hóa hơi ở nhiệt độ 1000C, biết rằng nhiệt độ cuối cùng của hỗn hợp là t = 240C. Nhiệt dung riêng