Ôn tập hình học lớp 9 chương III năm học 2015 - 2016

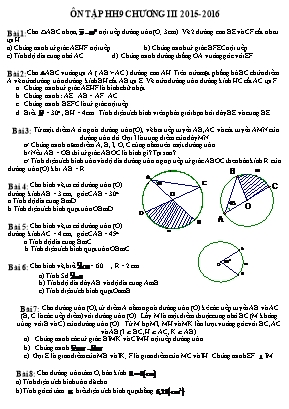
ÔN TẬP HH9 CHƯƠNG III 2015- 2016
Bài 1:Cho rABC nhọn, nội tiếp đường tròn (O; 3cm). Vẽ 2 đường cao BE và CF cắt nhau tại H.
a) Chứng minh tứ giác AEHF nội tiếp b) Chứng minh tứ giác BFEC nội tiếp
c) Tính độ dài cung nhỏ AC d). Chứng minh đường thẳng OA vuông góc với EF.
Bài 2:Cho ABC vuông tại A ( AB > AC ) đường cao AH. Trên nửa mặt phẳng bờ BC chứa điểm A vẽ nửa đường tròn đường kính BH cắt AB tại E. Vẽ nửa đường tròn đường kính HC cắt AC tại F.
Chứng minh tứ giác AEHF là hình chữ nhật.
Chứng minh : AE . AB = AF . AC.
Chứng minh BEFC là tứ giác nội tiếp.
Biết = 300 , BH = 4cm . Tính diện tích hình viên phân giới hạn bởi dây BE và cung BE
Bài 3: Từ một điểm A ở ngoài đường tròn (O), vẽ hai tiếp tuyến AB,AC và cát tuyến AMN của đường tròn đó. Gọi I là trung điểm của dây MN.
	a/ Chứng minh năm điểm A, B, I, O, C cùng nằm trên một đường tròn. 
	b/ Nếu AB = OB thì tứ giác ABOC là hình gì? Tại sao? 
	c/ Tính diện tích hình tròn và độ dài đường tròn ngoại tiếp tứ giác ABOC theo bán kính R của đường tròn (O) khi AB = R . 
Bài 4: Cho hình vẽ, ta có đường tròn (O) 
đường kính AB = 3 cm, góc CAB = 300.
a.Tính độ dài cung BmD.
b.Tính diện tích hình quạt tròn OBmD.
Bài 5: Cho hình vẽ, ta có đường tròn (O) 
đường kính AC = 4 cm, góc CAB = 450. 
	a.Tính độ dài cung BmC.
 b.Tính diện tích hình quạt tròn OBmC. 
Bài 6: Cho hình vẽ,biết = 60 , R = 2 cm. 
 a) Tính Sđ 
 b) Tính độ dài dây AB và độ dài cung AmB
 c) Tính diện tích hình quạt OamB
Bài 7: Cho đường tròn (O), từ điểm A nằm ngoài đường tròn (O) kẻ các tiếp tuyến AB và AC (B, C là các tiếp điểm) với đường tròn (O) . Lấy M là một điểm thuộc cung nhỏ BC (M không trùng với B và C) của đường tròn (O) . Từ M hạ MI, MH và MK lần lượt vuông góc với BC, AC và AB (I BC, H AC, K AB).
 Chứng minh các tứ giác BIMK và CIMH nội tiếp đường tròn.
 Chứng minh .
Gọi E là giao điểm của MB và IK; F là giao điểm của MC và IH. Chứng minh EF IM.
Bài 8: Cho đường tròn tâm O, bán kính 
a) Tính diện tích hình tròn đã cho	 
b) Tính góc ở tâm , biết diện tích hình quạt bằng 
c) Tính độ dài cung tròn l, biết diện tích hình quạt bằng 
Bài 9: Cho tam giác ABC vuông tại A. Trên AC lấy điểm M và vẽ đường tròn đường kính MC. Kẻ BM cắt đường tròn tại D. Đường thẳng DA cắt đường tròn tại S. Chứng minh rằng:
ABCD là tứ giác nội tiếp.
CA là tia phân giác của .
Chứng minh : DSMC DABC
Bài 10: Cho hình vẽ 
a) Tính số đo .
b) Tính độ dài cung AmB, cung ApB.
H2
H1
c) Tính diện tích hình quạt tròn AOBm
Bài 11: Cho tam giác ABC cân tại A. Các đường cao AG, BE, CF gặp nhau tại H.
a) Chứng minh tứ giác AEHF là tứ giác nội tiếp. Xác định tâm I của đường tròn ngoại tiếp tứ giác đó.
b) Chứng minh AF.AC = AH. AG
c) Chứng minh GE là tiếp tuyến của đường tròn tâm I.
Bài 12: Cho đường tròn (O), PA là tiếp tuyến của (O) tai A,B là giao của đoạn PO với đường tròn , sđ = 500. Tính số đo của góc PAB ?
Bài 13: Cho hình vẽ . 
Tính diện tích hình quạt tròn OAB có bán kính 5cm
Bài 14 : Cho DABC nhọn nội tiếp đường tròn (O), hai đường cao 
BM, CN của DABC cắt nhau tại H. Chứng minh:
	a) Tứ giác BCMN nội tiếp. Xác định tâm E của đường tròn ngoại tiếp tứ giác BCMN.
	b) DAMN ∽DABC
	c) Tia AO cắt d (O) tại K, cắt MN tại I. Chứng minh : Tứ giác BHCK là hình bình hành.
	d) Chứng minh: AK ^ MN
Bài 15: Cho đường tròn (O;R) và điểm S bên ngoài đường tròn sao cho SO = 2R. Vẽ các tiếp tuyến SA, SB của đường tròn (O;R) (A, B là các tiếp điểm), và cát uyến SMN (không qua O). Gọi I là trung điểm của MN.
 a) Chứng minh 5 điểm S, A, O, I, B cùng thuộc một đường tròn.
 b) Chứng minh : SA2 = SM . SN. 
 c)Tính SM, SN theo R khi MN = SA.
 d) Tính chu vi và diện tích hình phẳng giới hạn bởi SA, SB, .
 e) Kẻ MH OA, MH cắt AN, AB tại D và E. Chứng minh rằng E là trung điểm của MD.
Bài 16: Cho (O;R) và điểm S sao cho SO = 2R. Vẽ các tiếp tuyến SA, SB với (O) 
(A,B là các tiếp điểm) và cát tuyến SDE.
a/ Chứng minh: Tứ giác SAOB nội tiếp. Xác định tâm của đường tròn ngoại tiếp tứ giác đó 
b/ Chứng minh: góc SAD = góc SEA. 
c/ Chứng minh: SA2=SD.SE 
d/ Với R= 6cm. Tính số đo cung AB và diện tích hình quạt tròn OAB. 
e/ Tính diện tích hinh phẳng giới hạn bới SA, SB và cung ADB