Kỳ thi vào 10 năm học 2015 - 2016 môn toán thời gian làm bài 120 phút (không kể thời gian giao đề)

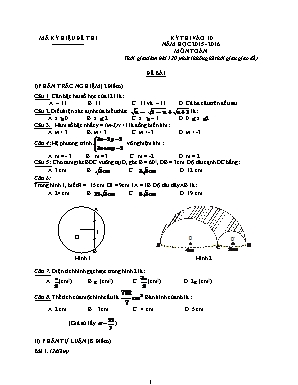
MÃ KÝ HIỆU ĐỀ THI
----------------
 KỲ THI VÀO 10 
NĂM HỌC 2015 - 2016
MÔN TOÁN
Thời gian làm bài 120 phút (không kể thời gian giao đề)
ĐỀ BÀI
I)PHẦN TRẮC NGHIỆM ( 2Điểm)
Câu 1. Căn bậc hai số học của 121 là:
 A. – 11 B. 11 C. 11 và – 11 D. Cả ba câu trên đều sai
Câu 2.Điều kiện xác định của biểu thức là : 
 A. x 0 B. x 2 C. x – 1 D. 0 x 2
 Câu 3. Hàm số bậc nhất y = (m-3)x +1 là đồng biến khi: 
 A. m > 3	 B. m - 3 	 D. m < -3 
Câu 4: Hệ phương trình vô nghiệm khi :
 A. m = - 3 B. m = 3 C. m = -2 D. m = 2
Câu 5: Cho tam giác BDC vuông tại D, góc B = 600, DB = 3cm. Độ dài cạnh DC bằng:
 A. 3 cm	 B. C . D. 12 cm
Câu 6: 
Trong hình 1, biết R = 15 cm. OI = 9cm. IA = IB. Độ dài dây AB là:
 A. 24 cm	 B. C . 	 D. 19 cm
I
B
A
O
 Hình 1 Hình 2
Câu 7. Diện tích hình gạch sọc trong hình 2 là:
 A. (cm2) B. p (cm2) C. (cm2) D. 2p (cm2)
Câu 8. Thể tích của một hình cầu là . Bán kính của nó là :
 A. 2 cm	 B. 3cm C . 4 cm	 D. 5 cm
	(Giả sử lấy )
II) PHẦN TỰ LUẬN (8 Điểm)
Bài 1. (2điểm)
1. Cho biểu thức : 
 a) Rút gọn A
 b) Tính A khi 
 2 .Giải bất phương trình sau: .
 3. Viết phương trình đường thẳng (d) : biết (d) đi qua điểm và vuông góc với đường thẳng 
Bài 2. (2 điểm)
1. Cho phương trình 
a) Giải phương trình khi m = 1
b) Tìm m để phương trình có 2 nghiệm thoả mãn : 
2. Một khu vườn hình chữ nhật có chu vi 40 mét, nếu tăng chiều dài 3 mét và giảm chiều rộng 2 mét thì chiều dài gấp 2 lần chiều rộng . Hỏi kích thước khu vườn đó là bao nhiêu ?
Bài 3: (3 điểm)
Cho (O;R) và điểm A nằm bên ngoài đường tròn. Kẻ các tiếp tuyến AB, AC với đường tròn (B, C là các tiếp điểm).
1) Chứng minh ABOC là tứ giác nội tiếp.
2) Gọi E là giao điểm của BC và OA. Chứng minh BE vuông góc với OA và OE.OA = R2
3) Trên cung nhỏ BC của (O;R) lấy điểm K bất kì (K khác B và C). Tiếp tuyến tại K của (O;R) cắt AB, AC theo thứ tự tại P và Q. Chứng minh tam giác APQ có chu vi không đổi khi K chuyển động trên cung nhỏ BC.
Bài 4: (1 điểm)
Chứng minh rằng: với mọi x, y >0 
 Cho a,b,c, là độ dài 3 cạnh của một tam giác. CMR: 
..................HẾT......................
PHẦN XÁC NHẬN
TÊN FILE: ĐỀ THI MÔN TOÁN VÀO LỚP 10 THPT
MÃ ĐỀ THI:.........................
TỔNG SỐ TRANG (ĐỀ THI VÀ HƯỚNG DẪN) LÀ 6 TRANG
NGƯỜI RA ĐỀ
(Ký, ghi rõ họ tên)
TỔ, NHÓM TRƯỞNG
(Ký, ghi rõ họ tên)
XÁC NHẬN CỦA BGH
(Ký, ghi rõ họ tên)
ĐÁP ÁN – THANG ĐIỂM
I. Trắc nghiệm: (2 điểm) Mỗi câu đúng được 0.25 điểm
Câu
1
2
3
4
5
6
7
8
Đáp án
B
D
A
C
C
A
D
B
II. Tự luận: ( 8 điểm)
Bài
ý
Nội dung
Điểm
1(2đ)
1
A
0,25
0,25
0,25
0,25
2
BPT tương đương với
Vậy PT có nghiệm là: 
0,25
0,25
3
Từ giả thiết ta có hệ PT: 
. 
Vậy đường thẳng cần tìm là: 
0,25
0,25
2(2đ)
1
a) với m = 1 phương trình có dạng 
PT có 2 nghiệm phân biệt: 
b) Pt đã cho có hai nghiệm phân biệt , thỏa mãn đề bài 
(I)
(I) 
 KL: m=7
0,25đ
0,25đ
0,25đ
0,25đ
0,25
2
 Gọi x, y (m) lần lượt là chiều rộng, chiều dài khu vườn hình chữ nhật (ĐK: 0 < x; y ) 
Theo đề bài ta có hệ phương trình:
 ( thoả mãn điều kiện)
 Vậy chiều rộng khu vườn là 9 (m); chiều dài là 11 (m).
0,25
0,25
0,25
3(3 đ)
 Hình vẽ
0,25
a.
Xét tứ giác ABOC có:
 = 900 (vì AB ^ OB do AB là tiếp tuyến của (O))
 = 900 (vì AC ^ OC do AC là tiếp tuyến của (O))
Þ ABOC là tứ giác nội tiếp ( tổng 2 góc đối bằng 1800 ) 
0,25
0,25
0,25
b.
DABC là tam giác cân tại A (vì AB, AC là hai tiếp tuyến của (O))
AO là phân giác (t/c hai tiếp tuyến cắt nhau)
ÞAO^ BC (t/c tam giác cân) Û AO ^ BE
0,25
0,25
0,25
Xét tam giác OBA vuông tại B:
Có : AO ^ BE (cmt)
ÞOE.OA = OB2 (hệ thức lượng trong tam giác vuông)
ÛOE.OA = R2
0,25
c
Xét (O):
PK = PB (t/c hai tiếp tuyến cắt nhau: PB, PK)
QK = QC(t/c hai tiếp tuyến cắt nhau: QK,QC)
 AP + PQ + QA = AP +( PK + KQ)+ QA
Þ AP + PB + AQ + QC= AB + AC luôn không đổi khi K di động trên cung nhỏ AC do AB, AC cố định
0,5
0,25
0,25
4( 1 đ)
a. 
Áp dụng BĐT côsi với 2 số dương x, y ta có: hay (1)
0,25
b.
do a + b – c > 0,......Áp dụng bất đẳng thức (1) ta có:
tương tự
Cộng 3 bất đẳng thức trên và suy ra đpcm
0,25
0,25
0,25
.....HẾT......................
PHẦN XÁC NHẬN
TÊN FILE: ĐỀ THI MÔN TOÁN VÀO LỚP 10 THPT
MÃ ĐỀ THI:.........................
TỔNG SỐ TRANG (ĐỀ THI VÀ HƯỚNG DẪN) LÀ 6 TRANG
NGƯỜI RA ĐỀ
(Ký, ghi rõ họ tên)
TỔ, NHÓM TRƯỞNG
(Ký, ghi rõ họ tên)
XÁC NHẬN CỦA BGH
(Ký, ghi rõ họ tên)