Kiểm tra học kỳ I năm 2015 - 2016 môn : Toán 8 thời gian: 90 phút ( không kể thời gian phát đề )

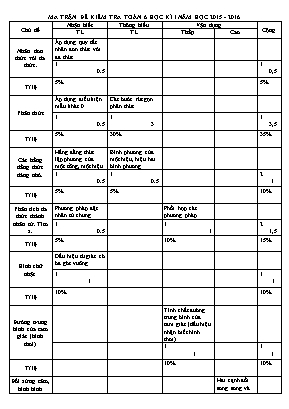
MA TRẬN ĐỀ KIỂM TRA TOÁN 6 HỌC KÌ I NĂM HỌC 2015 - 2016
Chủ đề
Nhận biết
Thông hiểu
Vận dụng
Cộng
TL
TL
Thấp
Cao
Nhân đơn thức với đa thức.
Áp dụng quy tắc nhân đơn thức với đa thức
1
0.5
1
 0,5
Tỉ lệ
5%
5%
Phân thức
Áp dụng điều kiện mẫu khác 0
Các bước rút gọn phân thức
1
0.5
1
 3
1
 3,5
Tỉ lệ
5%
30%
35%
Các hằng đẳng thức đáng nhớ.
Hằng đẳng thức lập phương của một tổng, một hiệu
Bình phương của một hiệu, hiệu hai bình phương
1
0.5
1
0.5
2
 1
Tỉ lệ
5%
5%
10%
Phân tích đa thức thành nhân tử. Tìm x.
Phương pháp đặt nhân tử chung
Phối hợp các phương pháp
1
0.5
1
1
2
 1,5
Tỉ lệ
5%
10%
15%
Hình chữ nhật
Dấu hiệu tứ giác có ba góc vuông
1
 1
1
 1
Tỉ lệ
10%
10%
Đường trung bình của tam giác (hình thoi)
Tính chất đường trung bình của tam giác (dấu hiệu nhận biết hình thoi)
1
 1
1
 1
Tỉ lệ
10%
10%
Đối xứng tâm, hình bình hành
Hai cạnh đối song song và bằng nhau
1
 1
1
 1
Tỉ lệ
10%
10%
Chia đa thức cho đơn thức.
Quy tắc chia đa thức cho đơn thức
1
 0.5
1
 0,5
Tỉ lệ
5%
5%
Cộng:
6
 3,5
2
 3,5
2
 2
1
 1
10
 10
Tỉ lệ: 35%
 35%
 20%
 10%
PHÒNG GD-ĐT MANG THÍT	 KIỂM TRA HỌC KỲ I NĂM 2015-2016
TRƯỜNG THCS CHÁNH AN 	 MÔN : TOÁN 8
 THỜI GIAN: 90 PHÚT ( Không kể thời gian phát đề ) 
Bài 1: (2đ) Thực hiện phép tính 
 	a) 2x2(3x2 + 5x + 7) 	b) (2x – 5)3	
c) 	d) (2x3y2 – 6x2y2 + 8x4y) : 2xy
Bài 2: (1đ) Phân tích đa thức thành nhân tử 
	a) x3y – x2y + xy2	b) x2 – 2x + 1 – 4y2 
Bài 3: (1đ): Tìm x, biết : x(x – 2009) + x – 2009 = 0	 
Bài 4: (3đ) Cho phân thức 
a) Tìm điều kiện của x để A là một phân thức
b) Rút gọn A.
Bài 5: (3đ) Cho tam giác ABC vuông tại A, đường cao AH. Gọi N là điểm đối xứng với H qua AB, P là giao điểm của NH và AB, M là điểm đối xứng của H qua AC, Q là giao điểm của MH và AC.
a) Chứng minh APHQ là hình chữ nhật. 
b) Chứng minh: AH =. 
c) Chứng minh 3 điểm M, A, N thẳng hàng.
 Hết
PHÒNG GD-ĐT MANG THÍT	 KIỂM TRA HỌC KỲ I NĂM 2015-2016
TRƯỜNG THCS CHÁNH AN 	 MÔN : TOÁN 8
 THỜI GIAN: 90 PHÚT ( Không kể thời gian phát đề ) 
Bài 1: (2đ) Thực hiện phép tính 
 	a) 2x2(3x2 + 5x + 7) 	b) (2x – 5)3	
c) 	d) (2x3y2 – 6x2y2 + 8x4y) : 2xy
Bài 2: (1đ) Phân tích đa thức thành nhân tử 
	a) x3y – x2y + xy2	b) x2 – 2x + 1 – 4y2 
Bài 3: (1đ): Tìm x, biết : x(x – 2009) + x – 2009 = 0	 
Bài 4: (3đ) Cho phân thức 
a) Tìm điều kiện của x để A là một phân thức
b) Rút gọn A.
Bài 5: (3đ) Cho tam giác ABC vuông tại A, đường cao AH. Gọi N là điểm đối xứng với H qua AB, P là giao điểm của NH và AB, M là điểm đối xứng của H qua AC, Q là giao điểm của MH và AC.
a) Chứng minh APHQ là hình chữ nhật. 
b) Chứng minh: AH =. 
c) Chứng minh 3 điểm M, A, N thẳng hàng.
 Hết
HƯỚNG DẪN CHẤM ĐIỂM
MÔN: TOÁN 8
Bài 1: (2đ) Thực hiện phép tính: 
 a) 2x2(3x2 + 5x + 7) = 6x4 + 10x3 + 14x2 ( 0,5đ)	
b) (2x - 5)3 = 8x3 - 60x2 + 150x - 125 	 (0,5đ)	
c) = (0,25đ)
= = 	(0,25đ)
d/ (2x3y2 – 6x2y2 + 8x4y) : 2xy = x2y – 3xy + 4x3 (0,5đ)
Bài 2 : (1đ) Phân tích đa thức thành nhân tử 
	a) x3y – x2y + xy2 = xy( x2 – x + y) 	(0,5đ)
	b)x2 – 2x + 1 – 4y2 = (x2 – 2x + 1) – (2y)2	(0,25đ)
 = (x – 1)2 – (2y)2 = ( x – 1 – 2y)(x – 1 + 2y)	(0,25đ)
Bài 3 : (1đ): Tìm x, biết : x(x – 2009) + x – 2009 = 0
	x(x – 2009) + ( x – 2009) = 0	
 (x – 2009)(x + 1) = 0 	(0,25đ)
Bài 4: (3đ) Cho phân thức: 
a) x3 – x 0 ó hoặc x 	(1,5đ)
b) A = 	(1,5đ)
Bài 5: 
a) Xét tứ giác APHQ, có:
 = 900 (do ∆ABC vuông tại A)	 	(0,25)	
= 900 (do HP AB)	(0,25)
 = 900 (do HQ AC)	(0,25)
=> Tứ giác APHQ là hình chữ nhật.	(0,25)
b) Xét ∆MHN, có:
NP = PH, HQ = QM (cmt) => PQ là đường trung bình 
=> PQ = 	(0,5)
Mà: APHQ là hình chữ nhật (cmt) => AH = PQ
Suy ra: AH = 	 	(0,5) 	
c) Có APHQ là hình chữ nhật (cmt)
+ PH = AQ, PH // AQ và AP = QH, AP //QH.
Mà N đối xứng với H qua AB (gt) => PH = NP
+ NP = AQ, NP // AQ => ANPQ là hình bình hành
+ AN // PQ (1)	(0,5)
Lại có: M đối xứng H qua AC (gt) => QH = QM 
 và AP = QH, AP //QH (cmt) => AMQP là hình bình hành
+ AM // QP (2)
Từ (1) và (2) => N, A, M thẳng hàng (Theo tiên đề Ơclit)	(0,5)