Kiểm tra học kì II năm học 2015 - 2016 môn: Toán 8 thời gian: 90 phút (không kể thời gian giao đề)

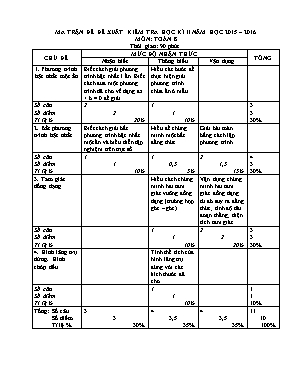
MA TRẬN ĐỀ ĐỀ XUẤT KIỂM TRA HỌC KÌ II NĂM HỌC 2015 – 2016
MÔN: TOÁN 8
Thời gian: 90 phút
CHỦ ĐỀ
MỨC ĐỘ NHẬN THỨC
TỔNG
Nhận biết
Thông hiểu
Vận dụng
1. Phương trình bậc nhất một ẩn
Biết cách giải phương trình bậc nhất 1 ẩn. Biết cách đưa một phương trình dã cho về dạng ax + b = 0 để giải
Hiểu các bước để thực hiện giải phương trình chứa ẩn ở mẫu
Số câu
Số điểm
Tỉ lệ %
2
2
20%
1
1
10%
3
3
30%
2. Bất phương trình bậc nhất
Biết cách giải bất phương trình bậc nhất một ẩn và biểu diễn tập nghiệm trên trục số
Hiểu để chứng minh một bất đẳng thức.
Giải bài toán bằng cách lập phương trình
Số câu
Số điểm
Tỉ lệ %
1
1
10%
1
0,5
5%
2
1,5
15%
4
3
30%
3. Tam giác đồng dạng
Hiểu cách chứng minh hai tam giác vuông đồng dạng (trường hợp góc – góc)
Vận dụng chứng minh hai tam giác đồng dạng từ đó suy ra đẳng thức; tính độ dài đoạn thẳng; diện tích tam giác
Số câu
Số điểm
Tỉ lệ %
1
1
10%
2
2
20%
3
3
30%
4. Hình lăng trụ đứng. Hình chóp đều
Tính thể tích của hình lăng trụ đứng với các kích thước đã cho
Số câu
Số điểm
Tỉ lệ %
1
1
10%
1
1
10%
Tổng: Số câu
 Số điểm
 Tỉ lệ %
3
3
30%
4
3,5
35%
4
3,5
35%
11
10
100%
KIỂM TRA HỌC KÌ II NĂM HỌC 2015-2016
MÔN: TOÁN 8
THỜI GIAN: 90 Phút (Không kể thời gian giao đề)
Câu 1: (3 điểm) Giải các phương trình sau: 
a) 3x - 9 = 0	
b) 3x + 2(x + 1) = 6x - 7	
c) 	
Câu 2: (1,5 điểm) Giải toán bằng cách lập phương trình:
Lúc 6 giờ sáng một ôtô khởi thành từ A để đi đến B. Đến 7 giờ 30 phút một ôtô thứ hai cũng khởi hành từ A để đi đến B với vận tốc lớn hơn vận tốc ôtô thứ nhất là 20km/h và hai xe gặp nhau lúc 10 giờ 30. Tính vận tốc mỗi ôtô? (ô tô không bị hư hỏng hay dừng lại dọc đường)
Câu 3: (1,5 điểm) 
a) Giải bất phương trình 7x + 4 ≥ 5x - 8 và biểu diễn tập hợp nghiệm trên trục số.
b) Chứng minh rằng nếu: a + b = 1 thì a2 + b2 
Câu 4: (1 điểm) 
Cho hình lăng trụ đứng ABC.A’B’C’ có chiều cao AA’ = 6cm, đáy là tam giác vuông có hai cạnh góc vuông AB = 4cm và AC = 5cm. Tính thể tích của hình lăng trụ.
Câu 5: (3 điểm) 
Cho tam giác ABC vuông ở A. Vẽ đường thẳng (d) đi qua A và song song với đường thẳng BC, BH vuông góc với (d) tại H .
a) Chứng minh ∆ABC ∆HAB.
b) Gọi K là hình chiếu của C trên (d). Chứng minh AH.AK = BH.CK
c) Gọi M là giao điểm của hai đoạn thẳng AB và HC. Tính độ dài đoạn thẳng HA và diện tích ∆MBC, khi AB = 3cm, AC = 4cm, BC = 5cm.
HẾT
(Cán bộ coi thi không giải thích gì thêm)
HƯỚNG DẪN CHẤM
Câu
Tóm tắt giải
Điểm
Câu 1: (3điểm)
a) Giải phương trình.
3x - 9 = 0 3x = 9 x = 3 
=> Tập nghiệm của phương trình là {3}
0,75
0,25
b) 3x + 2(x + 1) = 6x - 7 3x + 2x + 2 = 6x - 7 
 2 + 7 = 6x – 3x – 2x 9 = x x = 9
0,5
0,5
c) 	ĐK: x ≠ -1 và x ≠ 4
với x ≠ -1 và x ≠ 4 thì 
 => 5(x - 4) + 2x = 2(x + 1)
 5x = 22 x = 
Tập hợp nghiệm của phương trình là {}
0,25
0,25
0,25
0,25
Câu 2: (1,5điểm) 
- Gọi vận tốc (km/h) của ô tô thứ 1 là x (x > 0)
- Vận tốc của ô tô thứ 2 là: x + 20
- Đến khi hai xe gặp nhau (10 giờ 30 phút):
 + Thời gian đi của ô tô thứ 1: 4 giờ 30 phút = giờ
 + Thời gian đi của ô tô thứ 2: 3 giờ
- Quãng đường ô tô thứ 1 đi được: x
- Quãng đường ô tô thứ 2 đi được: 3(x + 20)
- Theo đề bài ta có phương trình: x = 3(x + 20)
- Giải ra ta được x = 40
- Trả lời: Vận tốc của ô tô thứ 1 là 40 (km/h)
 Vận tốc của ô tô thứ 2 là 60 (km/h)
0,25
0,5
0,5
0,25
Câu 3: (1,5 điểm) 
a) 7x + 4 ≥ 5x - 8 7x - 5x ≥ -8 - 4 2x ≥ -12 x ≥ - 6
tập hợp nghiệm của bất phương trình là {x/ x ≥ - 6}
- Biểu diễn đúng
0,5
0,25
0,25
b) Chứng minh rằng nếu: a + b = 1 thì a2 + b2 
Ta có: a + b = 1 => b = 1 - a => a2 + b2 = a2 + (1 - a)2 = 2a2 - 2a + 1
= 2(a - )2 + ≥ 
0,25
0,25
Câu 4: (1 điểm) 
+ ∆ABC vuông tại => diện tích ∆ABC là S = AB.AC 
=> S =4.5 = 10 (cm2) 
+ Thể tích lăng trụ đứng là V = S.h
=> V = 10.6 = 60 (cm3)
0,5
0,5
Câu 5: (3 điểm)
a) Xét 2∆: ABC và HAB có
+ = 900(gt); = 900 (AH ^ BH) => = 
+ = (so le)
=> ∆ABC ∆HAB
1
b) Xét 2∆: HAB và KCA có:
+ = 900 (CK ^ AK) => = 
+ + = 900(do = 900), + = 900 (∆HAB vuông ở H) => = 
=> ∆HAB ∆KCA
=> => AH.AK = BH.CK
1
c) có: ∆ABC ∆HAB (c/m a)
=> => => HA = cm
Có: 
+ AH // BC => => MA = => MA = MB
+ MA + MB = AB => MA + MB = 3cm
=> MB = 3 => MB = cm
+ Diện tích ∆MBC là S =AC.MB => S = .4. = (cm2)
0,5
0,5