Kiểm tra học kì II môn: Toán – Lớp 9 thời gian: 90 phút (không kể phát đề)

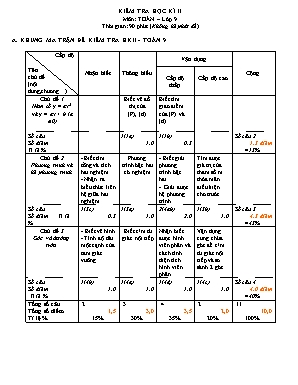
KIỂM TRA HỌC KÌ II
Môn: TOÁN – Lớp 9
Thời gian: 90 phút (Không kể phát đề)
A. KHUNG MA TRẬN ĐỀ KIỂM TRA HKII - TOÁN 9 
 Cấp độ
Tên 
chủ đề 
(nội dung,chương)
Nhận biết
Thông hiểu
Vận dụng
Cộng
Cấp độ thấp
Cấp độ cao
Chủ đề 1
Hàm số y = ax2 
 và y = ax + b (a0)
Biết vẽ đồ thị của 
(P), (d)
Biết tìm giao điểm của (P) và (d)
Số câu 
Số điểm 
Tỉ lệ %
1(1a)
1,0
1(1b)
0,5
Số câu 2
1,5 điểm
=15% 
Chủ đề 2
Phương trình và hệ phương trình
- Biết tìm tổng và tích hai nghiệm
- Nhận ra biểu thức liên hệ giữa hai nghiệm
Phương trình bậc hai có nghiệm
- Biết giải phương trình bậc hai.
- Giải được hệ phương trình
Tìm được giá trị của tham số m thỏa mãn điều kiện cho trước
Số câu 
Số điểm Tỉ lệ %
1(3c)
0,5
1(3a)
1,0
2(4ab)
2,0
1(3b)
1,0
Số câu 5
4,5 điểm
=45% 
Chủ đề 3
Góc và đường tròn
- Biết vẽ hình
- Tính độ dài một cạnh của tam giác vuông
Biết c/m tứ giác nội tiếp 
Nhận biết được hình viên phân và cách tính diện tích hình viên phân
Vận dụng cung chứa góc để c/m tứ giác nội tiếp và so sánh 2 góc 
Số câu 
Số điểm 
 Tỉ lệ %
1(4b)
1,0
1(4a)
1,0
1(4d)
1,0
1(4c)
1,0
Số câu 4
4,0 điểm
=40%
Tổng số câu 
Tổng số điểm
Tỉ lệ %
 2
 1,5
15%
 3
 3,0
30%
 4
 3,5
35%
 2
 2,0
20%
 11
10,0
100%
KIỂM TRA HỌC KÌ II
Môn: TOÁN – Lớp 9
Thời gian: 90 phút (Không kể phát đề)
Bài 1(1,5đ) 
a) Vẽ đồ thị của các hàm số sau trên cùng một mặt phẳng tọa độ :
; 
b) Tìm tọa độ giao điểm (nếu có) của (d) và (P).
Bài 2(2,0đ)
a) Giải phương trình 
Giải hệ phương trình 
Bài 3 (2,5đ) Cho phương trình: x2 – mx – 4 = 0 (m là tham số) (1)
Chứng minh phương trình (1) luôn có hai nghiệm phân biệt x1, x2 với mọi giá trị của m.
Tìm giá trị của m để phương trình (1) có hai nghiệm x1, x2 thỏa mãn điều kiện: 
Tìm hệ thức liên hệ giữa x1, x2 không phụ thuộc giá trị của m.
Bài 4 (4,0đ)
Từ một điểm M ở bên ngoài đường tròn (O ; 6cm); kẻ hai tiếp tuyến MN; MP với đường tròn (N ; P (O)) và cát tuyến MAB của (O) sao cho AB = 6 cm.
a) Chứng minh: OPMN là tứ giác nội tiếp
b) Tính độ dài đoạn thẳng MN biết MO = 10 cm
c) Gọi H là trung điểm đoạn thẳng AB. So sánh góc với góc 
d) Tính diện tích hình viên phân giới hạn bởi cung nhỏ AB và dây AB của hình tròn tâm O đã cho.
--------Hết--------
KIỂM TRA HỌC KÌ II
Môn: TOÁN – Lớp 9
Thời gian: 90 phút (Không kể phát đề)
C. HƯỚNG DẪN CHẤM: 
ĐÁP ÁN
BIỂU ĐIỂM
Bài 1: 
a)Vẽ đồ thị
Tọa độ điểm của đồ thị 
x
-2
-1
0
1
2
4
1
0
1
4
Tọa độ điểm của đồ thị 
x
0
3
0
(1,5điểm)
0,25
0,25
0,5
b)Phương trình hoành độ giao điểm của (P) và (d)
Có dạng a – b + c = 1 – (-2) + (-3) = 0
 từ (P) 
Vậy : Tọa độ giao điểm của (P) và (d) là 
0,25
0,25
Bài 2: 
a) 
D = (-5)2 – 4.3 = 25 – 12 = 13 > 0 
Vì D > 0 nên phương trình có 2 nghiệm phân biệt
(2,0điểm)
0,5
0,25
0,25
b) 
1,0
Bài 3: Cho phương trình: x2 – mx + m – 1 = 0 (m là tham số) (1)
a) C/m: Phương trình (1) luôn có nghiệm với mọi giá trị của m.
=> Phương trình (1) luôn có nghiệm với mọi giá trị của m
(2,5điểm)
0,25
0,25
0,25
0,25
b) Tìm giá trị của m để phương trình (1) có hai nghiệm x1, x2 thỏa mãn điều kiện: 
+ Theo Viet: x1 + x2 = = m ; x1.x2 = = m – 1 
+ 
 m2 – 2.(m – 1) = 5 
 m2 – 2m + 2 = 5
 m2 – 2m – 3 = 0 
Phương trình có dạng: a – b + c = 1 – (- 2) + (-3) = 0 
Nên: m1 = -1; m2 = 3 
Vậy: m1 = -1 hoặc m2 = 3 thì phương trình (1) có hai nghiệm x1, x2 thỏa mãn điều kiện: 
0,25
0,25
0,25
0,25
c) Tìm hệ thức liên hệ giữa x1, x2 không phụ thuộc giá trị của m.
Ta có: x1 + x2 – 1 = x1.x2 x1 + x2 – x1.x2 = 1 
Vậy: Hệ thức liên hệ giữa x1, x2 không phụ thuộc giá trị của m là: x1 + x2 – x1.x2 = 1
0,25
0,25
Bài 4:
Vẽ hình đúng
(4,0điểm)
0,5
a) Tứ giác PMNO có = 900 và = 900 (Tính chất tiếp tuyến)
 + = 1800 Tứ giác PMNO nội tiếp 
0,5
0,5
b) Tính độ dài đoạn MN: 
Áp dụng định lí Py-Ta –go vào tam giác vuông MON ta có 
 MN = = = 8 cm
0,5
c) Vì: H là trung điểm của AB, nên: OH AB 
= = 900 
 và cùng nhìn đoạn OM một góc 900
 Tứ giác MNHO nội tiếp 
 = ( vì cùng chắn cungMN)
0,25
0,25
0,25
0,25
d) Gọi diện tích cần tính là SVP
	SVP = 
+ Ta có: 0A = OB = AB = 6cm => đều => = 915,59 + = 
	=>SVP = = 6 - 9 = 3(2 - 3) 18,84 - 15,59 3,25 (cm2) 
0,25
0,25
0,25
0,25
* Học sinh có thể giải cách khác, nếu đúng vẫn cho điểm tối đa
--------Hết--------