Kiểm tra 1 tiết lần 1 học kì II năm học 2015 - 2016 môn: Đại số – lớp 11 – Thời gian: 45 phút

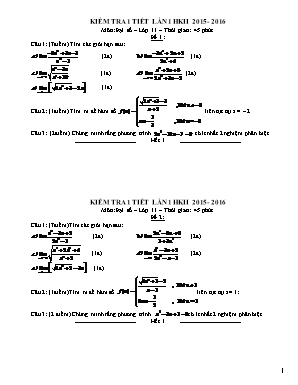
KIỂM TRA 1 TIẾT LẦN 1 HKII 2015 - 2016 
Môn:Đại số – Lớp 11 – Thời gian: 45 phút
Đề 1:
Câu 1: (7điểm) Tìm các giới hạn sau:
	 (2đ)	 (1đ)
	 (1đ)	 (2đ)
 (1đ)
Câu 2: (1điểm) Tìm m để hàm số liên tục tại x = – 2 
Câu 3: (2điểm) Chứng minh rằng phương trình có ít nhất 2 nghiệm phân biệt	
Hết !
KIỂM TRA 1 TIẾT LẦN 1 HKII 2015 - 2016 
Môn:Đại số – Lớp 11 – Thời gian: 45 phút
Đề 2:
Câu 1: (7điểm)Tìm các giới hạn sau:
	 (2đ)	 (2đ)
 (1đ) 	 (2đ)
 (1đ)	 
Câu 2: (1điểm)Tìm m để hàm số liên tục tại x= 1:
Câu 3: (2 điểm) Chứng minh rằng phương trình 	 có ít nhất 2 nghiệm phân biệt
Hết !
ĐÁP ÁN KIỂM TRA 1 TIẾT LẦN 1 HKII MÔN TOÁN 11 - ĐỀ 1 / 2016
CÂU 
NỘI DUNG + ĐÁP ÁN 
ĐIỂM
1
2,0
 (HS có thể chia cả tử và mẫu cho )
1.0
1.0
1,0
0.5
Do và 
0.5
1,0
0.5
0.5
2,0
1.0
1.0
1,0
0.25
0.25
0.5
2
Tìm m để hàm số liên tục tại x = – 2
1,0
TXĐ: D = R
Ta có: 
0.25
Và 
0.5
Để hàm số f(x) liên tục tại x = – 2 thì 
0.25
Vậy 	
3
Chứng minh rằng phương trình có ít nhất 2 nghiệm phân biệt trên 
2,0
Xét hàm số 
0.25
Ta có : 
0.5
Do đó, và 
0.5
y = f(x) là hàm đa thức nên liên tục trên .
 Do đó f(x) liên tục trên các đoạn 
0.25
Từ đó suy ra phương trình f(x) = 0 có ít nhất 1 nghiệm và 1 nghiệm .
0.25
Vậy phương trình có ít nhất 2 nghiệm phân biệt
0.25
10,0
ĐÁP ÁN KIỂM TRA 1 TIẾT LẦN 1 HKII MÔN TOÁN 11 - ĐỀ 2/2016
CÂU 
NỘI DUNG + ĐÁP ÁN 
ĐIỂM
1
2,0
0.5
0.5
1,0
0.5
Do và 
0.5
1,0
0.25
0.5
2,0
1.0
0.5
0.5
0.25
0.25
0.5
2
Tìm m để hàm số liên tục tại x= 1
1,0
TXĐ: D = R
0.25
Ta có: 
Và 
0.5
Để hàm số f(x) liên tục tại x = 1 thì 
0.25
Vậy 	
3
Chứng minh rằng phương trình có ít nhất 2 nghiệm phân biệt trên 
2,0
Xét hàm số 
0.25
Ta có : 
0.5
Do đó, và 
0.5
y = f(x) là hàm đa thức nên liên tục trên .
 Do đó f(x) liên tục trên các đoạn 
0.25
Từ đó suy ra phương trình f(x) = 0 có ít nhất 1 nghiệm và 1 nghiệm .
0.25
Vậy phương trình có ít nhất 2 nghiệm phân biệt trên 
0.25
10,0