Kiểm tra 1 tiết Hình 7 (tiết 46)

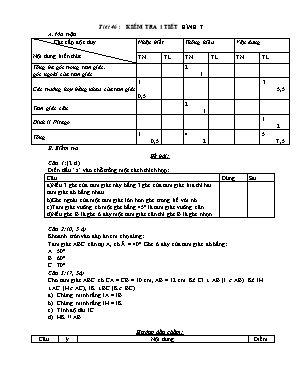
TiÕt 46 : KiÓm tra 1 tiÕt HÌNH 7
A. Ma trận
 Các cấp độ t duy
Nội dung kiến thức
Nhận biết
Thông hiểu
Vận dụng
TN
TL
TN
TL
TN
TL
Tổng ba góc trong tam giác, 
góc ngoài của tam giác
2
 1
Các trường hợp bằng nhau của tam giác
1
 0,5
 3
 5,5
Tam giác cân
2
 1
Định lí Pitago
1
 2
Tổng
1
 0,5 
4
 2
5
 7 ,5
B. Kiểm tra
Đề bài:
Câu 1: (2 đ)
Điền dấu “x” vào chỗ trống một cách thích hợp:
Câu
Đúng
Sai
a)Nếu 3 góc của tam giác này bằng 3 góc của tam giác kia thì hai tam giác đó bằng nhau
b)Góc ngoài của một tam giác lớn hơn góc trong kề với nó
c)Tam giác vuông có một góc bằng 450 là tam giác vuông cân
d)Nếu góc B là góc ở đáy một tam giác cân thì góc B là góc nhọn
..............
..............
..............
..............
..............
..............
..............
..............
Câu 2: (0, 5 đ)
Khoanh tròn vào đáp án em chọ đúng:
Tam giác ABC cân tại A, có Â = 400. Góc ở đáy của tam giác đó bằng:
500 
600
700
Câu 3: (7, 5đ) 
Cho tam giác ABC có CA = CB = 10 cm, AB = 12 cm. Kẻ CI ^ AB (I Î AB). Kẻ IH ^AC (HÎ AC), IK ^BC (KÎ BC).
Chứng minh rằng IA = IB
Chứng minh rằng IH = IK
Tính độ dài IC
HK // AB
Hướng dẫn chấm:
Câu
ý
Nội dung
Điểm
1
a)
b)
c)
d)
Sai
Sai
Đúng
Đúng
0,5
0,5
0,5
0,5
2
C
0,5
3
a)
b)
c)
d)
Vẽ hình, ghi GT, KL đúng 
Xét ∆AIC và ∆BIC có
CI cạnh chung
Þ∆AIC = ∆BIC(cạnh huyền – cạnh góc vuông)
ÞIA = IB (cạnh tương ứng)
Xét ∆IHC và ∆IKC có:
CI là cạnh chung
Þ∆IHC = ∆IKC (cạnh huyền – góc nhọn)
ÞIH = IK (cạnh tương ứng)
Từ IA = IB (chứng minh trên)
Mà AB = 12 cm
ÞIA = IB = 6cm
áp dụng định lí Pitago vào tam giác vuông AIC, ta có
IA2 + IC2 = AC2
ÞIC2 = AC2 - IA2 = 102 – 62 = 100 – 36 = 64
ÞIC = 8 cm
Chứng minh được CI ^AB
Chứng minh được CI ^AB
Kết luận HK// AB
Chú ý: HS có thể làm theo cách khác
0,5
1,0
0,5
0,5
1,0
0,5
0,5
0,5
0,5
1,0
0,5
0,5