Kì thi chọn học sinh giỏi lớp 11 thpt năm học 2010-2011 đề thi môn: Vật lý (dành cho học sinh thpt chuyên ) thời gian làm bài: 180 phút, không kể thời gian giao đề

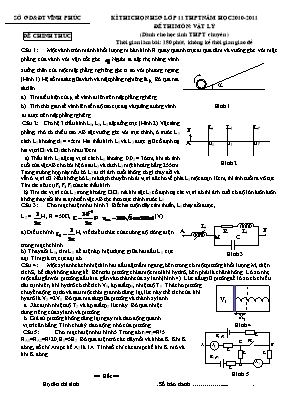
Së gd&®t vÜnh phóc
§Ò CHÝNH THøC
K× THI CHäN HSG LíP 11 THPT N¡M HäC 2010-2011
§Ò THI M¤N: VËT Lý 
(Dµnh cho häc sinh THPT chuyªn )
Thêi gian lµm bµi: 180 phót, kh«ng kÓ thêi gian giao ®Ò
a
Câu 1: Một vành tròn mảnh khối lượng m bán kính R quay quanh trục đi qua tâm và vuông góc với mặt phẳng của vành với vận tốc góc .Người ta đặt nhẹ nhàng vành xuống chân của một mặt phẳng nghiêng góc a so với phương ngang (Hình 1). Hệ số ma sát giữa vành và mặt phẳng nghiêng là m. Bỏ qua ma sát lăn.
Tìm điều kiện của m để vành đi lên trên mặt phẳng nghiêng.
Tính thời gian để vành lên đến độ cao cực đại và quãng đường vành Hình 1
 đi được trên mặt phẳng nghiêng. 
 B
A
L1
L2
L3
O1
O2
O3
Hình 2
Câu 2: Cho hệ 3 thấu kính L1, L2, L3 đặt đồng trục (Hình 2). Vật sáng phẳng, nhỏ có chiều cao AB đặt vuông góc với trục chính, ở trước L1 cách L1 khoảng d1 = 45cm. Hai thấu kính L1 và L3 được giữ cố định tại hai vị trí O1 và O3 cách nhau 70cm.
 a) Thấu kính L2 đặt tại vị trí cách L1 khoảng 0102 = 36cm, khi đó ảnh cuối của vật AB cho bởi hệ ở sau L3 và cách L3 một khoảng bằng 255cm. Trong trường hợp này nếu bỏ L2 đi thì ảnh cuối không có gì thay đổi và vẫn ở vị trí cũ. Nếu không bỏ L2 mà dịch chuyển nó từ vị trí đã cho về phía L3 một đoạn 10cm, thì ảnh cuối ra vô cực. Tìm các tiêu cự f1, f2, f3 của các thấu kính.
 b) Tìm các vị trí của L2 trong khoảng O1O3 mà khi đặt L2 cố định tại các vị trí đó thì ảnh cuối có độ lớn luôn luôn không thay đổi khi ta tịnh tiến vật AB dọc theo trục chính trước L1.
Câu 3: A
B
R
L1
C
L2
M
Hình 3
Cho mạch điện như hình 3. Biết hai cuộn dây cảm thuần, L1 thay đổi được, 
L2 = H, R = 50Ω, , (V). 
a) Điều chỉnh H, viết biểu thức của cường độ dòng điện trong mạch chính.
b) Thay đổi L1, tìm L1 để điện áp hiệu dụng giữa hai đầu L1 cực đại. Tìm giá trị cực đại đó.
Câu 4:Hình 4
l0
X0
V1
 Một xylanh cách nhiệt kín hai đầu đặt nằm ngang, bên trong có một pittông khối lượng M, diện tích S, bề dày không đáng kể. Bên trái pittông chứa một mol khí hydrô, bên phải là chân không. Lò xo nhẹ một đầu gắn với pittông, đầu kia gắn vào thành của xy lanh (hình 4). Lúc đầu giữ pitông để lò xo có chiều dài tự nhiên, khí hydrô có thể tích V1, áp suất p1, nhiệt độ T1. Thả cho pittông chuyển động tự do và sau một thời gian nó dừng lại, lúc này thể tích của khí hyđrô là V2 =2V1. Bỏ qua ma sát giữa pittông và thành xylanh. 
 a. Xác định nhiệt độ T2 và áp suất p2 lúc này. Bỏ qua nhiệt 
dung riêng của xylanh và pittông.
 b. Giả sử pittông không dừng lại ngay mà dao động quanh
R
E2,r2
E1,r1
A
K
D
A1
A2
B
C
R
R
R
R
 vị trí cân bằng. Tính chu kỳ dao động nhỏ của pittông.
 Câu 5: Cho mạch điện như hình 5 Trong đó r1=r2=R/5 RA1=RA2=R/20; E1=5E2. Bỏ qua điện trở các dây nối và khóa K. Khi K đóng, số chỉ Ampe kế A2 là 1A. Tính số chỉ các ampe kế khi K mở và khi K đóng. 
Hình 5
== Hết ==
Họ tên thí sinh . Số báo danh ......................
ĐÁP ÁN ĐỀ CHÍNH THỨC KÌ THI HSG LỚP 11 (CHUYÊN )NĂM 2011
MÔN VẬT LÝ
Câu 1: (2 điểm)
a) Do vận tốc đầu của khối tâm bằng không nên khi vừa đặt xuống vành vừa quay vừa trượt trên mặt phẳng nghiêng. Phương trình động lực học cho khối tâm là
Fms-mgsia =ma => mmgcosa-mgsina =ma => a=g(mcosa-sina) 
Để vành đi lên mặt phẳng nghiêng thì a>0 do đó m >tana (0,5 đ)
N
P
Fms
b) Vận tốc khối tâm tăng dần trong khi vận tốc góc giảm dần, đến thời điểm v=ωR thì vành sẽ lăn không trượt. Do đó ta xét vành đi lên gồm hai giai đoạn:
* Giai đoạn vừa quay vừa trượt:
- Phương trình chuyển động là: -FmsR=mR2.g => g=-mgcosa/R 
Đến thời điểm t1 vành kết thúc trượt thì vận tốc khối tâm và vận tốc góc bằng nhau: 
v1=at1=g(mcosa-sina)t1; 
ω1= ω0+ gt1= ω0 –mgcosa.t1/R (0,25 đ)
Do v1=ω1R suy ra t1=; v1=at1=(mcosa-sina)
ω1 =(mcosa-sina) 
Quãng đường mà vành đi lên được trong giai đoạn này là
S1=v12/2a = (0,5 đ)
* Giai đoạn vành lăn không trượt: Lực ma sát nghỉ hướng lên trên:
Phương trình động lực học cho khối tâm và phương trình quay quanh tâm tức thời: 
-mgRsina =2mR2.g => g =-gsina /2R
Gia tốc khối tâm của vành là a=gR=-gsina /2
Thời gian chuyển động lên trong giai đoạn này xác định từ phương trình 0=v1+a’t2
=> t2=(mcosa-sina) (0,5 đ)
Quãng đường vành lên được trong giai đoạn này là
S2= -v12/2a’ = (mcosa-sina)2 
=> Thời gian và quãng đường đi lên là t=t1+t2 và s=s1+s2 (0,25 đ)
Câu 2(2 điểm): 
a) Tìm các tiêu cự f , f, f của các thấu kính.
- Ta có:
+ Sơ đồ tạo ảnh với hệ ba thấu kính:
+ Sơ đồ tạo ảnh với hệ hai thấu kính (L), ( L):
Vì: 	=; d = d nên: d= d d= d= 0
Ta có: 	d= O1O2- d d = O1O2= 36(cm)
	 	d = O2O3 - d d= O2O3 = 34(cm) (0,25đ)
Tiêu cự của thấu kính (L):
	f1== = 20(cm) (0,25đ)
Tiêu cự của thấu kính (L):
f3 = = =30(cm) (0,25đ)
Khi dịch chuyển (L) ta có sơ đồ tạo ảnh bởi (L) (vị trí mới) và ( L) như sau:
Vì dd33= f3= 30(cm)
Mà: 	d33 = OO3 - dd= OO - d= 24 - 30 = - 6(cm)
	d= OO- d = 46 - 36 = 10(cm)
Tiêu cự của thấu kính (L):
	f2 == = - 15(cm) (0,25đ)
b) Tìm các vị trí của (L) trong khoảng O1O3 :
- Khi tịnh tiến vật AB trước thấu kính (L1), tia tới từ B song song với trục chính không đổi. Có thể coi là tia này do một điểm vật ở vô cực trên trục chính phát ra.
Nếu ảnh sau cùng có độ lớn không đổi, ta có một tia ló khỏi ( L3) song song với trục chính cố định. Có thể coi tia này tạo điểm ảnh ở vô cực trên trục chính. Hai tia này tương ứng với nhau qua hệ thấu kính.
Ta có: 	d d= f1 = 20(cm)
d d= f3 = 30(cm) (0,25đ)
Gọi x là khoảng cách từ (L1) đến (L2) thỏa yêu cầu đề bài, ta có:
	d2 = x -d = x - 20	(1)	
 	d3 = 70 – x - d = 30	(2) (0,25đ)
Từ (1) và (2) ta được: 	70 - x - = 30
70x - 350 - x + 5x + 15x - 300 = 30x - 150x- 60x + 500 = 0 (*) (0,25đ)
Phương trình (*) cho ta 2 giá trị: x = 50 (cm), x = 10 (cm) (0,25đ)
Câu 3 (2 điểm):
a) ; ; . (0,25đ)
* UMB sớm pha so với iR góc j1 = .
* Gọi jMB là độ lệch pha giữa i và uMB:
® i sớm pha 0,25p so với uMB. (0,25đ)
* Từ giản đồ: ® ® 
* UAB = = I.
® I = 
 = = 2A (0,25đ)
Gọi j là độ lệch pha giữa uAB và i:
tanj = = = 0 ® j = 0
Vậy phương trình dòng điện trong mạch chính: i = 2cos100pt (A). (0,25đ)
b) Độ lệch pha giữa uMB và i không phụ thuộc vào L1 và luôn bằng 0,25p.
Ta có giản đồ véc tơ như hình vẽ.
Từ giản đồ, áp dụng định lí sin: (0,25đ)
® 
Dễ thấy UL1 lớn nhất « sina lớn nhất « a = 900. (0,25đ)
DOMN vuông cân ® UL1max = UMB= UAB = 100 (V) (0,25đ)
I = A ® ZL1 = 100W ® L1 = H (0,25đ)
Câu 4(2 điểm): 
a) * Trạng thái khí ban đầu khi pittông bắt đầu CĐ: V1, p1,T1
* Trạng thái khí khi pittông dừng lại: V2 = 2V1, p2, T2
 + Do xylanh cách nhiệt : Q = A+ ΔU = 0 (1) 
Trong đó (2) 	
+ VTCB, lò xo bị nén một đoạn X0 = h/2 
 lực đàn hồi tác dụng lên pittông : (0,25đ)	
+ Áp lực của khí trong xy lanh tác dụng lên pittông: 
 F2 = p2 .S
+ Phương trình trạng thái cho một mol khí hydrô: 
 p2V2 = R.T2 với V2 = 2V1 = 2S.X0 
Suy ra (0,25đ)	
+ Pittông đứng yên : F1= F2 
+ Công khí thực hiện lên pittông bằng công của Fđh (AFdh=A) 
 (3) 	 
+ Thay (2) ,(3) vào (1) được : T2 = T1 (0,25đ)	 
+ Phương trình cho 2 trạng thái : p1.V1 = R.T1 
 và p2.V2 = p2.2V1 = RT2 
x
0
h
x
Fđh
F
 Suy ra : (0,25đ)	
b) Tại vị trí cân bằng: 
 p2 S = k.X0 và V2 = Sh (4)
 + Tại li độ x<<h  : F – Fđh = M.x’’ 
 hay pS – k(X0 + x) =M.x’’ (5) 	 
Quá trình đoạn nhiệt: 
 (0,25đ) 	 
+ Do x << h nên (6) (0,25đ)	
Thay (4),(6) vào (5) ta có: (0,25đ)	
Vậy khi li độ x << h, Pittông dao động gần điều hòa với chu kì 
 = (0,25đ)	
Câu 5 (2 điểm): 
R
I1
E2,r2
E1,r1
A
D
A1
A2
B
C
R
I2
IA1
IA2
R
I3
R
R
* Khi K đóng các dòng điện có chiều như hình vẽ. Ta có:
I3=UDB/R => I3=IA2.(RA+R)/R=21/20A
I2=I3+IA2=41/20 A 
UAB=3,51R-E2 (1) 
=> IA1=UAB/(R+RA) =70,2/21 -20E2/21R (2)
=> I1=I2+IA1=2265/420-20E2/21R (0,5đ)
Mặt khác UAB=E1-I1(r1+R) =5E2 -453R/70 -120E2/105 	(3) 
R
I1
E2,r2
E1,r1
A
A1
D
I2
IA1
2R
2R
A2
Từ (1) và (3) rút ra: E2/R =2,055 	(4) 
Từ (4) và (2) ta có: IA1=1,386 A (0,5đ)
* Khi K mở, điện trở của các đoạn mạch AE1BD; AE2D và ACD lần lượt là:
R1=2R+r1+RA =45R/20 
R2=R+r2+RA =6R/5 
R3=2R+RA =41R/20 	(0,5đ)
Chú ý đến (4) và E1=5E2, áp dụng định luật Ôm tổng quát cho các đoạn mạch ta suy ra:
UAD=(E1/R1-E2/R2) / (1/R1+1/R2+1/R3) =1,539/R
=> IA1=UAD/R3=0,75A; IA2=I1=(E1-UAD)/R1=3,88A 	(0,5đ)
-------------------------------------------------------------------
*-Nếu thí sinh làm cách khác vẫn đúng thì cho điểm tối đa tương ứng.
 *-Thí sinh không viết hoặc viết sai đơn vị từ hai lần trở lên thì trừ 0,25 điểm cho toàn bài.