Giáo án lớp 12 môn Toán - Tuần 2: Khảo sát hàm số trùng phương và bài toán liên quan

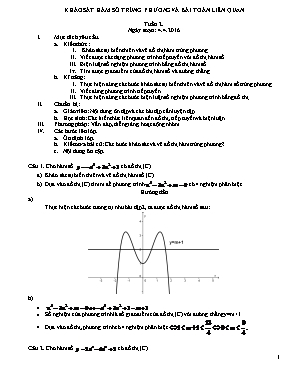
KHẢO SÁT HÀM SỐ TRÙNG PHƯƠNG VÀ BÀI TOÁN LIÊN QUAN
Tuần 2. 
Ngày soạn: 4.4.2016. 
Mục đích yêu cầu. 
Kiến thức:
 Khảo sát sự biến thiên và vẽ đồ thị hàm trùng phương. 
Viết được các dạng phương trình tiếp tuyến với đồ thị hàm số. 
Biện luận số nghiệm phương trình bằng đồ thị hàm số. 
Tìm được giao điểm của đồ thị hàm số và đường thẳng.
Kĩ năng: 
Thực hiện đúng các bước khảo sát sự biến thiên và vẽ đồ thị hàm số trùng phương.
Viết đúng phương trình tiếp tuyến. 
Thực hiện đúng các bước biện luận số nghiệm phương trình bằng đồ thị.
Chuẩn bị: 
Giáo viên: Nội dung ôn tập và các bài tập cần luyện tập. 
Học sinh: Các kiến thức liên quan đến đồ thị, tiếp tuyến và biện luận. 
Phương pháp: Vấn đáp, diễn giảng, hoạt động nhóm.
Các bước lên lớp.
Ổn định lớp. 
Kiểm tra bài cũ: Các bước khảo sát và vẽ đồ thị hàm trùng phương?
Nội dung ôn tập.
Câu 1. Cho hàm số có đồ thị (C)
Khảo sát sự biến thiên và vẽ đồ thị hàm số (C).
Dựa vào đồ thị (C) tìm m để phương trình có 4 nghiệm phân biệt.
Hướng dẫn
a)
	Thực hiện các bước tương tự như bài tập 2, ta được đồ thị hàm số sau:
b)
Số nghiệm của phương trình là số giao điểm của đồ thị (C) với đường thẳng y=m+1.
Dựa vào đồ thị, phương trình có 4 nghiệm phân biệt 
Câu 2. Cho hàm số có đồ thị (C). 
Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số. 
Tìm số thực m để phương trình có bốn nghiệm phân biệt.
Hướng dẫn
Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số. 
Tập xác định: 
Hàm số đồng biến trên khoảng (-1;0) và (1;+). 
Hàm số nghịch biến trên khoảng (-;-1) và (0;1).
Hàm số đạt cực đại tạo x=0, y=2. 
Hàm số đạt cực tiểu tại , y=0. 
Bảng biến thiên: 
Đồ thị.
Tìm số thực m để phương trình có bốn nghiệm phân biệt.
Ta có: 
Số nghiệm phương trình (*) bằng với số giao điểm của đồ thị (C) và đường thẳng d: y=-2m+2. 
Để phương trình (*) có bốn nghiệm phân biệt khi và chỉ khi đường thẳng d cắt đồ thị (C) tại bốn điểm phân biệt. 
Khi và chỉ khi 
Câu 3. Cho hàm số 
Khảo sát sự biến thiên và vẽ đồ thị hàm số (1) khi m = 2.
Tìm tất cả các giá trị m để hàm số có cực đại và cực tiểu.
Hướng dẫn
Khảo sát sự biến thiên và vẽ đồ thị hàm số (1) khi m = 2.
Với m = 2, 
TXĐ: D = 
; 
Hàm số đồng biến trên các khoảng (-1; 0) và (1; )
Hàm số nghịch biến trên các khoảng (-; -1) và (0; 1)
Hàm số đạt cực đại tại x = 0; ycđ = y(0) = 0
Hàm số đạt cực tiểu tại x = 1; yct = y(1) = -2.
-Giới hạn tại vô cực:+.
Tìm tất cả các giá trị m để hàm số có cực đại và cực tiểu.
Để hàm số có cực đại và cực tiểu khi và chỉ khi m>1. 
Câu 4. Cho hàm số , với m là tham số thực. Tìm m để đồ thị hàm số (1) có hai điểm cực trị. 
	Hướng dẫn
Để hàm số có cực đại và cực tiểu 
Câu 5. Tìm giao điểm của đồ thị hàm số và đường thẳng.
Hướng dẫn
Phương trình hoành độ giao điểm của đồ thị hàm số và đường thẳng là: 
 Với x=2 suy ra y=1. 
 Giao điểm cần tìm là: A(2;1).
Viết tiếp tuyến của đồ thi hàm số (C) khi biết trước hệ số góc của nó.
+ Gọi là tiếp điểm, giải phương trình , 
+ Đến đây trở về dạng 1,ta dễ dàng lập được tiếp tuyến của đồ thị: 
*) Tiếp tuyến song song với đường thẳng (d): y = ax + b. Khi đó hệ số góc k = a.
*) Tiếp tuyến vuông góc với đường thẳng (d): y = ax + b.
*) Tiếp tuyến tạo với đường thẳng (d): y = ax + b một góc . Khi đó, .
Câu 6. Cho hàm số (C). Viết phương trình tiếp tuyến của đồ thị (C) biết hệ số góc của tiếp tuyến k = -3.
Giải:
Ta có: 
Gọi là tiếp điểm Tiếp tuyến tại M có hệ số góc 
Theo giả thiết, hệ số góc của tiếp tuyến k = - 3 nên: 
Vì .
Phương trình tiếp tuyến cần tìm là .
Câu 7. Viết phương trình tiếp tuyến của đồ thị hàm số (C). Biết tiếp tuyến đó song song với đường thẳng y = 9x + 6.
Giải:
Ta có: 
Gọi là tiếp điểm Tiếp tuyến tại M có hệ số góc 
Theo giả thiết, tiếp tuyến đó song song với đường thẳng y = 9x + +6 tiếp tuyến có hệ số góc k = 9 
Phương trình tiếp tuyến của (C) tại M(-1;-3) là: (loại)
Phương trình tiếp tuyến của (C) tại M(3;1) là: 
Câu 8. Cho hàm số (C). Viết phương trình tiếp tuyến của (C) biết tiếp tuyến đó vuông góc với đường thẳng .
Giải:
Ta có . Do tiếp tuyến của (C) biết tiếp tuyến đó vuông góc với đường thẳng nên hệ số góc của tiếp tuyến k = 9.
 Do đó 
+) Với x = 2 . Pttt tại điểm có hoành độ x = 2 là: 
+) Với . Pttt tại điểm có hoành độ x = - 2 là: .
 Vậy có hai tiếp tuyến củả (C) vuông góc với đường thẳng là: y =9x - 14 và y = 9x + 18.
Câu 9. Lập phương trình tiếp tuyến với đồ thị (C) của hàm số: , biết tiếp tuyến vuông góc với đường thẳng (d): .
Giải:
	(d) có phương trình: nên (d) có hệ số góc là -.
Gọi là tiếp tuyến cần tìm có hệ số góc k thì .
Ta có: nên hoành độ tiếp điểm là nghiệm phương trình: 
Vậy tiếp điểm M có tọa độ là 
Tiếp tuyến có phương trình: 
Vậy tiếp tuyến cần tìm có phương trình: . 
Câu 10. Cho hàm số (C). Viết phương trình tiếp tuyến với (C) biết rằng tiếp tuyến cắt trục hoành tại A, trục tung tại B sao cho tam giác OAB vuông cân tại O, ở đây O là góc tọa độ.
Giải
Ta có: 
Vì tiếp tuyến tạo với hai trục tọa độ một tam giác vuông cân nên hệ số góc của tiếp tuyến là: 
Khi đó gọi là tiếp điểm của tiếp tuyến với đồ thị (C) ta có 
Với thì lúc đó tiếp tuyến có dạng (trường hợp này loại vì tiếp tuyến đi qua góc tọa độ, nên không tạo thành tam giác OAB)
Với thì lúc đó tiếp tuyến có dạng 
Vậy tiếp tuyến cần tìm là 
Câu 11. Cho hàm số y = có đồ thị (C).
 Lập phương trình tiếp tuyến của đồ thị (C) sao cho tiếp tuyến này cắt các trục Ox, Oy lần lượt tại các điểm A và B thỏa mãn OA = 4OB.
Giải
 	Giả sử tiếp tuyến d của (C) tại cắt Ox tại A, Oy tại B sao cho .
Do DOAB vuông tại O nên Þ Hệ số góc của d bằng hoặc .
Hệ số góc của d là Û 
Khi đó có 2 tiếp tuyến thỏa mãn là: .
Tiếp tuyến đi qua điểm 
	Cho đồ thị (C): y = f(x). Viết phương trình tiếp tuyến với (C) biết tiếp tuyến đi qua điểm .
Cách giải
	+ Tiếp tuyến có phương trình dạng: , (với x0 là hoành độ tiếp điểm).
	+ Tiếp tuyến qua nên 
 + Giải phương trình (*) để tìm x0 rồi suy ra phương trình tiếp tuyến.
Câu 12. Cho đồ thị (C): , viết phương trình tiếp tuyến với (C) biết tiếp tuyến đi qua điểm A(-2; -1).
Giải:
	Ta có: 
Gọi M là tiếp điểm. Hệ số góc của tiếp tuyến là .
Phương trình tiếp tuyến với (C) tại M là : 
 qua A(-2;-1) nên ta có: 
Vậy có hai tiếp tuyến cần tìm có phương trình là: 
Củng cố: Các bước khảo sát vẽ đồ thị hàm số, các bước viết phương trình tiếp tuyến, các bước biện luận nghiệm phương trình bằng đồ thị? 
Dặn dò: 
Học các bước khảo sát vẽ đồ thị hàm trùng phương, học các bước viết phương trình tiếp tuyến, các bước biện luận nghiệm phương trình bằng đồ thị? 
Chuẩn bị tiết sao ôn tập phương trình mũ và phương trình lôgarit: Học trước các công thức lũy thừa và cách giải phương trình mũ. 
Bài tập tự luyện 
Cho hàm số . Viết phương trình tiếp tuyến tại điểm có hoành độ x = 1 
Cho hàm số , viết phương trình tiếp tuyến biết tiếp tuyến vuông góc với đường thẳng 
Cho hàm số . trong tất cả các tiếp tuyến của (C ) tìm tiếp tuyến có hệ số góc nhỏ nhất 
Cho hàm số: (C). Tính diện tích hình phẳng giới hạn bởi (C), trục Oy và tiếp tuyến của (C) tại điểm có hoành độ x = 3.
Cho hàm số . Viết phương trình tiếp tuyến của đồ thị (C) biết tiếp tuyến đó vuông góc với đường thẳng d: 
Lập phương trình tiếp tuyến với đồ thị (C) của hàm số . Biết tiếp tuyến đi qua điểm A(-1; 3).
Cho hàm số: y = có đồ thị (C). Viết phương trình tiếp tuyến của (C) đi qua A(-6,5) 
Lập phương trình tiếp tuyến của đồ thị (C) của hàm số y = 2x3 + 3x2 - 12x - 1 kẻ từ điểm 
Cho hàm số có đồ thị (C).
a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số (C) 
b) Tìm trên (C) những điểm M sao cho tiếp tuyến tại M của (C) cắt hai tiệm cận của (C) tại A, B sao cho AB ngắn nhất
Cho hàm số: . CMR: 
	a) Nếu tiếp tuyến của đths cắt hai đường tiệm cận tại A và B thì tiếp điểm là trung điểm của AB.
 	b) Mọi tiếp tuyến của đồ thị đều tạo với hai đường tiệm cận một tam giác có diện 
tích không đổi. 
 	c) Tìm tất cả các điểm thuộc đồ thị hàm số sao cho tiếp tuyến tại đó tạo với hai đường tiệm cận một tam giác có chu vi nhỏ nhất.
Cho hàm số .Tìm m để tiếp tuyến của tại giao điểm của nó với trục tung tạo với hai trục tọa độ một tam giác có diện tích bằng 8.
Cho hàm số: 
a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số.
	b) Tìm những điểm M trên (C) sao cho tiếp tuyến với (C) tại M tạo với hai trục tọa độ một tam giác có trọng tâm nằm trên đường thẳng 4x + y = 0.