Đề thi thử tốt nghiệp thpt quốc gia năm học: 2014 - 2015 môn: Toán - Đề 2 thời gian làm bài : 180 phút

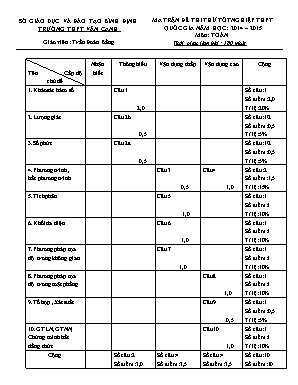
SỞ GIÁO DỤC VÀ ĐÀO TẠO BÌNH ĐỊNH 
TRƯỜNG THPT VÂN CANH
Giáo viên : Trần Đồn Bằng
MA TRẬN ĐỀ THI THỬ TỐT NGHIỆP THPT QUỐC GIA NĂM HỌC: 2014 – 2015
Mơn: TỐN
 Thời gian làm bài : 180 phút
Tên Cấp độ
chủ đề
Nhận biết
Thơng hiểu
Vận dụng thấp
Vận dụng cao
Cộng
1.Khảo sát hàm số
Câu 1
 2,0
Số câu:1
Số điểm:2,0 
Tỉ lệ:20%
2.Lượng giác
Câu 2b 
 0,5
Số câu:1/2
Số điểm:0,5 
Tỉ lệ:5%
3.Số phức
Câu 2a
 0,5
Số câu:1/2
Số điểm:0,5 
Tỉ lệ:5%
4.Phương trình ,
bất phương trình
Câu 3
 0,5
Câu 4
 1,0
Số câu:2
Số điểm:1,5 
Tỉ lệ:15%
5.Tích phân
Câu 5
 1,0
Số câu:1
Số điểm:1 
Tỉ lệ:10%
6.Khối đa diện
Câu 6
 1,0
Số câu:1
Số điểm:1 
Tỉ lệ:10%
7.Phương pháp tọa độ trong khơng gian
Câu 7
 1,0
Số câu:1
Số điểm:1 
Tỉ lệ:10%
8.Phương pháp tọa độ trong mặt phẳng
Câu 8
 1,0
Số câu:1
Số điểm:1 
Tỉ lệ:10%
9.Tổ hợp ,Xác suất
Câu 9
 0,5
Số câu:1
Số điểm:0,5 
Tỉ lệ:5%
10.GTLN,GTNN,
Chứng minh bất đẳng thức
Câu 10
 1,0
Số câu:1
Số điểm:1 
Tỉ lệ:10%
Cộng
Số câu:2
Số điểm:3,0 
Tỉ lệ:30%
Số câu:4
Số điểm:3,5
Tỉ lệ:35%
Số câu:4
Số điểm:3,5
Tỉ lệ:35%
Số câu:10
Số điểm:10
Tỉ lệ:100%
SỞ GIÁO DỤC VÀ ĐÀO TẠO BÌNH ĐỊNH 
TRƯỜNG THPT VÂN CANH
Giáo viên : Trần Đồn Bằng
ĐỀ THI THỬ TỐT NGHIỆP THPT QUỐC GIA 
NĂM HỌC: 2014 - 2015
Mơn: TỐN-ĐỀ 2
 Thời gian làm bài : 180 phút
Câu 1 (2,0 điểm)Cho hàm số 
a. Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số.
b. Lập phương trình đường thẳng đi qua điểm cực đại của đồ thị (C) và vuơng gĩc với tiếp tuyến của đồ thị (C) tại gốc tọa độ.
Câu 2 (1, 0 điểm)
a. Tìm phần thực và phần ảo của số phức z thoả mãn điều kiện 
b. Cho là gĩc mà tan=2. Tính 
Câu 3 (0,5 điểm) Giải phương trình: 
Câu 4 (1, 0 điểm) Giải bất phương trình 
Câu 5 (1, 0 điểm) Tính: 
Câu 6 (1,0 điểm)Cho khối chĩp S.ABC cĩ cạnh bên SA vuơng gĩc với đáy. Mặt bên (SBC) tạo với đáy gĩc 600. Biết SB = SC = BC = a. Tính thể tích khối chĩp S.ABC theo a.
Câu 7 (1,0 điểm)Trong khơng gian với hệ tọa độ Oxyz, cho mặt cầu (S): x2 + y2 + z2 - 4x + 2y + 4z - 7 = 0 và 
mặt phẳng (α) : x - 2y + 2z + 3 = 0 
a. Tính khoảng cách từ tâm I của mặt cầu (S) tới mặt phẳng (α). 
b. Viết phương trình mặt phẳng (β) song song với mặt phẳng (α) và tiếp xúc với mặt cầu (S).
Câu 8(1,0 điểm)Trong mặt phẳng với hệ tọa độ Oxy,cho hình vuơng ABCD cĩ M(1;2) là trung điểm AB, N(-2;1) là điểm thuộc đoạn AC sao cho AN=3NC.Viết phương trình của đường thẳng CD
Câu 9(0,5 điểm) Đề cương ơn tập cuối năm mơn Tốn lớp 12 cĩ 40 câu hỏi.Đề thi cuối năm gồm 3 câu hỏi trong số 40 câu đĩ.Một học sinh chỉ ơn 20 câu trong đề cương.Giả sử các câu hỏi trong đề cương đều cĩ khả năng được chọn làm câu hỏi thi như nhau.Hãy tính xác suất để cĩ ít nhất 2 câu hỏi của đề thi cuối năm nằm trong số 20 câu hỏi mà học sinh nĩi trên đã ơn.
Câu 10(1,0 điểm)Cho các số thực khơng âm a,b,c thõa mãn a+b+c =1.Tìm giá trị nhỏ nhất của biểu thức
------------------------------------Hết----------------------------
ĐÁP ÁN VÀ BIỂU ĐIỂM ĐỀ 1
Nội dung
Điểm
Câu 1(2,0điểm)
a.
(1,0
điểm)
+Tập xác định 
+Chiều biến thiên -----------------------------------------------------------------------
+Cực trị 
+Giới hạn --------------------------------------------------------------------------
+BBT ----------------------------------------------------------------------------
+Đồ thị -------------------------------------------------------------------------------
0,25
0,25
0,25
0,25
b
(1,0 điểm)
+ Điểm Cực đại của ( C ) là M(1;4/3)--------------------------------------------------
+T.T của ( C ) tại gốc toạ độ cĩ hệ số gĩc k= y’(0)=3--------------------------------
+Đường thẳng cần tìm đi qua điểm M và cĩ hệ số gĩc k’= -1/3 nên cĩ pt:
 y= - 1/3(x-1)+4/3=-1/3x+5/3------------------------------------------------
0,25
0,25
0,5
Câu 2(1,0 điểm)
a
(0,5 điểm)
Giả sử ,z=x+yi(x,y ).Ta cĩ 
 ĩx+yi +(2+i)(x-yi)=3+5i
 ĩ3x+y+(x-y)i=3+5i
 ĩ ------------------------------------------
Vậy phần thực và phần ảo của số phức z lần lượt bằng 2,-3--------------------------------
0,25
0,25
b.
(0,5 điểm)
-------------------------------------------------------------
 =-----------------------------------
0,25
0,25
Câu 3(0,5 điểm)
ĩ
ĩ
ĩ----------------------------------------------------------------------
ĩ----------------------------------------------------------
0,25
0,25
Câu 4(1,0 điểm)
ĐK: 
 ĩ
 ĩ(vì>0)----------------
 ĩ
 ĩ
 ĩ---------------------------------------------------
 ------------------------------------------------
So sánh với điều kiện , ta cĩ nghiệm của bất phương trình là--------
0,25
0,25
0,25
0,25
Câu 5(1,0 điểm)
Đặt .
Khi đĩ I=.
 =.
0,25
0,25
0,5
Câu 6(1,0 điểm)
(Hình vẽ)
Vẽ đường cao AH của tam giác ABC.
Khi đĩ BC SC (định lí 3 đường vuơng gĩc)
Và gĩc SHA là gĩc giữa mặt bên (SBC) và mặt đáy.
Từ gt,ta cĩ gĩc SHA bằng 600------------------------------------------------------------------------------------------------
Vì tam giác SBC là tam giác đều cạnh a nên SH =
Ta lại cĩ AH =SH cos600=,SA=SH sin600= ---------------------------------------
Vậy thể tích của khối chĩp S.ABC
 V=1/3 SA.SABC=1/6.SA.AH.BC= --------------------------------
0,25
0,25
0,5
Câu 7(1,0 điểm)
 a.
(S) cĩ tâm I(2;-1;-2) và bán kính R=4 ----------------------------------------------------------
Do đĩ d(I,())=1 -----------------------------------------------------------------------------
0,25
0,25
b.
Viết phương trinh mặt phẳng (β) song song với mặt phẳng (α) và tiếp xúc với mặt cầu (S).
Vì mặt phẳng (β) song song với mặt phẳng (α) nên pt của (β) cĩ dạng 
 x-2y+2z+D=0 --------------------------------------------------
Ta cĩ d(I, (β))=R
ĩ ĩ
Vậy (β) cĩ pt là x-2y+2z+12=0 hoặc x-2y+2z-12=0 -----------------------------------------
0,25
0,25
Câu 8(1,0 điểm)
Ta cĩ MN= ,AN=3AC/4= 
MN2=AM2+AN2-2AM.AN.cos450= 
=>a=4---------------------------------------------------------------------------------------------
Gọi I(x;y) là trung điểm của CD.Ta cĩ 
 ------------------------------------------------------
+Đường thẳng CD đi qua I(1;-2) cĩ pt : y+2=0------------------------------------------
+ Đường thẳng CD đi qua I(17/5;-6/5) cĩ pt : 3x-4y-15=0-----------------------------
0,25
0,25
0,25
0,25
Câu 9(0,5 điểm)
Khơng gian mẫu cĩ
 n()= (phần tử)
Gọi A là biến cố “cĩ ít nhất 2 câu hỏi của đề thi nằm trong số 20 câu đã ơn”.Ta thấy xảy ra một trong hai TH sau
TH1: Trong đề thi cĩ đúng 2 câu hỏi trong 20 câu đã ơn
TH2: Trong đề thi cĩ đúng 3 câu hỏi trong 20 câu đã ơn
Do đĩ n(X)= (phần tử)-------------------------------------------------
Vậy xác suất cần tìm: P(X)=
0,25
0,25
Câu 10(1,0 điểm)
Đặt t=ab+bc+ca ( ),ta cĩ
a2+b2+c2 ab+bc+ca
=>1=(a+b+c)2= a2+b2+c2+2(ab+bc+ca) 3(ab+bc+ca)=3t
=> a2+b2+c2=1-2t với 
Theo bất đẳng thức Cơ-si
T2=(ab+bc+ca)2 3(a2b2+b2c2+c2a2)
Do đĩ M t2+3t+2 ---------------------------------------------------------------
Xét hàm số f(t)= t2+3t+2 trên tập ,
f’(t)= 
f’’(t)= 
=>f’(t) nghịch biến trên D
=>f’(t)f’(1/3)= => f(t)đồng biến trên D
=>f(t) f(0)=2 ---------------------------------------------------------------------------------
Vậy minM =2 đạt được khi t=0,tức là với a,b,c khơng âm thõa mãn
a,b,c là một trong các bộ số (0;0;1),(0;1;0),(1;0;0)---------------------------------
0,25
0,5
0,25
SỞ GIÁO DỤC VÀ ĐÀO TẠO BÌNH ĐỊNH 
TRƯỜNG THPT VÂN CANH
Giáo viên : Trần Đồn Bằng
ĐỀ THI THỬ TỐT NGHIỆP THPT QUỐC GIA 
NĂM HỌC: 2014 - 2015
Mơn: TỐN-ĐỀ 2
 Thời gian làm bài : 180 phút
Câu 1 (2,0 điểm)Cho hàm số 
a. Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số.
b.Tìm k để đường thẳng (d) : y=kx+2k+1 cắt (C) tại 2 điểm phân biệt.
Câu 2 (1, 0 điểm)
a. Cho gĩc thõa mãn : và . Tính 
b. Tìm mơđun của số phức z thoả mãn điều kiện 
Câu 3 (0,5 điểm) Giải phương trình: 
Câu 4 (1, 0 điểm) Giải bất phương trình 
Câu 5 (1, 0 điểm) Tính: 
Câu 6 (1,0 điểm)Cho khối chĩp S.ABCD cĩ đáy ABCD là hình vuơng cạnh a , SA=a.Hình chiếu vơng gĩc của đỉnh S trên mặt phẳng (ABCD) là điểm H thuộc đoạn AC , .Gọi CM là đường cao của Chứng minh M là trung điểm của SA và thể tích khối tứ diện SMBC theo a.
Câu 7 (1,0 điểm) Trong khơng gian với hệ tọa độ Oxyz, cho mặt cầu 
(S): x2 + y2 + z2 - 4x + 2y + 4z - 7 = 0 , đường thẳng d : 
a. Viết phương trình mặt phẳng (P) vuơng gĩc với đường thẳng d và tiếp xúc với mặt cầu (S).
b. Viết phương trình đường thẳng đi qua tâm của mặt cầu (S), cắt và vuơng gĩc với đường thẳng d.
Câu 8(1,0 điểm)
Trong mặt phẳng với hệ tọa độ Oxy,cho 2 đường thẳng d: x+y=0 và d’: x-y=0.Gọi (C) là đường trịn tiếp xúc với d tại A,cắt d’ tại 2 điểm B,C sao cho tam giác ABC vuơng tại B.Viết phương trình của (C) biết diện tích tam giác ABC bằng và A cĩ hành độ dương.
Câu 9(0,5 điểm) Cho số nguyên dương n thõa điều kiện .
Tìm hệ số của x13 trong khai triển (x+3)3n
Câu 10(1,0 điểm)Cho các số thực khơng âm a,b,c thõa mãn a+b+c =1.Tìm giá trị nhỏ nhất của biểu thức
------------------------------------Hết----------------------------
ĐÁP ÁN VÀ BIỂU ĐIỂM ĐỀ 2
Nội dung
Điểm
Câu 1(2,0điểm)
a.
(1,0
điểm)
+Tập xác định 
+Chiều biến thiên -----------------------------------------------------------------------
+Cực trị -------------------------------------------------------------------------
+Giới hạn , tiệm cận --------------------------------------------------------------
+BBT ----------------------------------------------------------------------------
+Đồ thị -------------------------------------------------------------------------------
0,25
0,25
0,25
0,25
b
(1,0 điểm)
Xét pt =kx+k+1
 kx2+(3k-1)x+2k=0(x-1)
 kx2+(3k-1)x+2k=0 ( vì x=-1 khơng phải là nghiệm của pt với mọi k)
Do đĩ d cắt ( C ) tại 2 điểm phân biệt -------------------------
 ĩ-------------------------------
Vậy với k thõa (*) thì thõa yêu cầu bài tốn
0,25
0,25
0,5
Câu 2(1,0 điểm)
a
(0,5 điểm)
Giả sử ,z=x+yi(x,y ).Ta cĩ 
 ĩx+yi +(2+i)(x-yi)=3+5i
 ĩ3x+y+(x-y)i=3+5i
 ĩ ------------------------------------------
Vậy z=2-3i
 Do đĩ mơđun của số phức z lần lượt bằng --------------------------------
0,25
0,25
b.
(0,5 điểm)
Ta cĩ 
 Vì nên sin <0
Do đĩ --------------------------------------------------------------------------
Vậy =------------------------------
0,25
0,25
Câu 3(0,5 điểm)
ĩ
ĩ-----------------------------------------------------------------
ĩ
ĩ----------------------------------------------------------------------------------
0,25
0,25
Câu 4(1,0 điểm)
ĐK: 
 ĩ
 ĩ(vì>0)----------------
 ĩ
 ĩ
 ĩ---------------------------------------------------
 ------------------------------------------------
So sánh với điều kiện , ta cĩ nghiệm của bất phương trình là--------
0,25
0,25
0,25
0,25
Câu 5(1,0 điểm)
Đặt u= =>u2= 1+3lnx
2udu= -------------------------------------------------------
Đổi cận : x=e => u=2
 x=1 => u=1
Khi đĩ I=.
 =.
0,25
0,25
0,5
Câu 6(1,0 điểm)
(Hình vẽ )
+ C/m M là trung điểm của SA. 
Ta tính được
 SH= 
 SC=
Do đĩ tam giác SCA cân tại C nên M là trung điểm của SA
+ Tính thể tích khối tứ diện SMBC theo a
Ta vẽ MK vuơng gĩc với AC tại K,khi đĩ KM=SH/2
 VS.ABC=1/3 SH.SABC= --------------------------------
Khi đĩ
VMSBC =VMABC=1/2 VS.ABC=
0,25
0,25
0,5
Câu 7(1,0 điểm)
 a.
d cĩ một vtcp , (S) cĩ tâm I(2;-1;-2) và bán kính R=4
Vì (P) vuơng gĩc với d nên (P) nhận làm vtpt .Do đĩ pt của (P) cĩ dạng
x+2y-z+D=0----------------------------------------------------------------
Mặt khác (P) tiếp xúc với (S) nên ta cĩ 
d(I,(P))=Rĩĩ
Vậy pt của (P) là x+2y-z-2+=0 hoặc x+2y-z-2-=0-----------------------------
0,25
0,25
b.
Pt của d được viết dưới dạng tham số
Gọi d’ là đt cần tìm,và H(t ;1+2t ;2-t) là giao điểm của d và d’
Ta cĩ 
Và ĩt-2+2(2+2t)-(4-t)=0ĩt=1/3
Vậy H(1/3 ;5/3 ;5/3) ------------------------------------------------------------------------------
Do đĩ d’ đi qua 2 điểm I(2;-1;2) và H(1/3 ;5/3 ;5/3)
Vậy pt đt cần tìm -----------------------------------------------------------------
0,25
0,25
Câu 8(1,0 điểm)
Ta thấy đường trịn (C ) là đường trịn ngoại tiếp tam giác vơng ABC,cĩ đường kính AC
Điểm A thuộc d nên A(a;-a ) (a>0).
+Đường thẳng AB đi qua A và vuơng gĩc với d’ cĩ pt: x+y+2a=0
Do đĩ B là giao điểm của AB với d’ .khi đĩ B 
+ Đường thẳng AC đi qua A và vuơng gĩc với d cĩ pt: x-y-4a=0
Do đĩ C là giao điểm của AC với d’ .khi đĩ C ------------------------------
Ta lại cĩ S = =>a= 
Vậy -------------------------------------------------------------
Do đĩ đường trịn (C ) cĩ tâm là trung điểm của AC và bán kính R=IA=1
Vậy pt của( C): -----------------------------------------------
0,25
0,25
0,5
Câu 9(0,5 điểm)
Đặt S = 
Ta cĩ 
Do đĩ 
=> 
Vậy ---------------------------
Với n=5 , ta cĩ (x+3)3n=(x+3)15 .
Vậy hệ số của x13 trong khai triển (x+3)15 là ----------------------------------
0,25
0,25
Câu 10(1,0 điểm)
Đặt t=ab+bc+ca ( ),ta cĩ
a2+b2+c2 ab+bc+ca
=>1=(a+b+c)2= a2+b2+c2+2(ab+bc+ca) 3(ab+bc+ca)=3t
=> a2+b2+c2=1-2t với 
Theo bất đẳng thức Cơ-si
T2=(ab+bc+ca)2 3(a2b2+b2c2+c2a2)
Do đĩ M t2+3t+2 ---------------------------------------------------------------------
Xét hàm số f(t)= t2+3t+2 trên tập ,
f’(t)= 
f’’(t)= 
=>f’(t) nghịch biến trên D
=>f’(t)f’(1/3)= => f(t)đồng biến trên D
=>f(t) f(0)=2-----------------------------------------------------------------------------------
Vậy minM =2 đạt được khi t=0,tức là với a,b,c khơng âm thõa mãn
a,b,c là một trong các bộ số (0;0;1),(0;1;0),(1;0;0)------------------------------------
0,25
0,5
0,25