Đề thi thử kỳ thi thpt quốc gia môn : Toán thời gian làm bài 180 phút

NMHIEUPDP.WORDPRESS.COM ĐỀ THI THỬ KỲ THI THPT QUỐC GIA
———————— Môn : TOÁN
Đáp án đề số 01 Thời gian làm bài 180 phút
————
Câu 1a (1,0 điểm).
Với m = 1 hàm số trở thành y = −x3 + 3x2 − 1.
• Tập xác định : D = R.
• Sự biến thiên :
+ Giới hạn tại vô cực :
lim
x→+∞
y = −∞; lim
x→−∞
y = +∞.
+ Bảng biến thiên :
y′ = −3x2 + 6x = −3x(x− 2); y′ = 0⇔
[
x = 0
x = 2
.
x − ∞ 0 2 + ∞
y′ − 0 + 0 −
y
+ ∞
−1
3
− ∞
Hàm số đồng biến trên khoảng (0; 2).
Hàm số nghịch biến trên (−∞; 0) và (2; +∞).
Hàm số đạt cực đại tại x = 2; yCĐ = 3.
Hàm số đạt cực tiểu tại x = 0; yCT = −1.
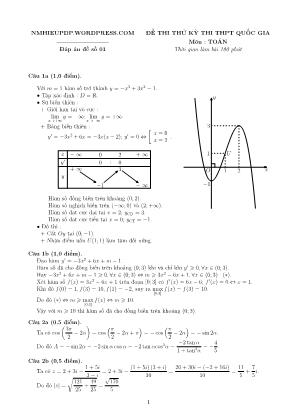
• Đồ thị :
+ Cắt Oy tại (0;−1).
+ Nhận điểm uốn U(1; 1) làm tâm đối xứng.
y
xO
−1
1
3
1 2
U
Câu 1b (1,0 điểm).
Đạo hàm y′ = −3x2 + 6x+m− 1.
Hàm số đã cho đồng biến trên khoảng (0; 3) khi và chỉ khi y′ > 0,∀x ∈ (0; 3).
Hay −3x2 + 6x+m− 1 > 0,∀x ∈ (0; 3)⇔ m > 3x2 − 6x+ 1,∀x ∈ (0; 3) (∗).
Xét hàm số f(x) = 3x2 − 6x+ 1 trên đoạn [0; 3] có f ′(x) = 6x− 6; f ′(x) = 0⇔ x = 1.
Khi đó f(0) = 1, f(3) = 10, f(1) = −2, suy ra max
[0;3]
f(x) = f(3) = 10.
Do đó (∗)⇔ m > max
[0;3]
f(x)⇔ m > 10.
Vậy với m > 10 thì hàm số đã cho đồng biến trên khoảng (0; 3).
Câu 2a (0,5 điểm).
Ta có cos
(
3pi
2
− 2α
)
= cos
(pi
2
− 2α + pi
)
= − cos
(pi
2
− 2α
)
= − sin 2α.
Do đó A = − sin 2α = −2 sinα cosα = −2 tanαcos2α = −2 tanα
1 + tan2α
= −4
5
.
Câu 2b (0,5 điểm).
Ta có z = 2 + 3i− 1 + 5i
3− i = 2 + 3i−
(1 + 5i) (3 + i)
10
=
20 + 30i− (−2 + 16i)
10
=
11
5
+
7
5
i.
Do đó |z| =
√
121
25
+
49
25
=
√
170
5
.
1
Câu 3 (0,5 điểm).
Phương trình đã cho tương đương với :
(2 + log2x)
2 − 6log2x− 7 = 0⇔ log22 x− 2log2x− 3 = 0⇔
[
log2x = −1
log2x = 3
⇔
[
x =
1
2
x = 8
Vậy phương trình đã cho có hai nghiệm x =
1
2
; x = 8.
Câu 4 (1,0 điểm).
Xét hệ

2x+
1
x
+ y +
2
y
= 6 (1)
(x2 + y2)
(
1 +
1
xy
)2
= 8 (2)
.
Điều kiện x 6= 0; y 6= 0.
Ta có (1)⇔ 2x+ y + 2x+ y
xy
= 6⇔ (2x+ y)
(
1 +
1
xy
)
= 6⇔ 1 + 1
xy
=
1
2x+ y
.
Thay vào (2) được 36 (x2 + y2) = 8(2x+ y)2 ⇔ 4x2 − 32xy + 28y2 = 0⇔
[
x = y
x = 7y
.
Với x = y thay vào (1) được 3x+
3
x
= 6⇔ x2 − 2x+ 1 = 0⇔ x = 1⇒ y = 1 (thỏa mãn).
Với x = 7y thay vào (1) được 15y +
15
7y
= 6⇔ 35y2 − 14y + 5 = 0 (vô nghiệm).
Vậy hệ có nghiệm duy nhất (x; y) = (1; 1).
Câu 5 (1,0 điểm).
Ta có I =
2∫
1
x+ 2 lnx
(x+ 2)2
dx =
2∫
1
x
(x+ 2)2
dx+
2∫
1
2 lnx
(x+ 2)2
dx = I1 + I2.
Trong đó
I1 =
2∫
1
x
(x+ 2)2
dx =
2∫
1
(
1
x+ 2
− 2
(x+ 2)2
)
dx =
(
ln |x+ 2|+ 2
x+ 2
)∣∣∣∣2
1
= ln
4
3
− 1
6
Đặt
u = lnxdv = 2
(x+ 2)2
dx
⇒

du =
1
x
dx
v = − 2
x+ 2
, ta có
I2 = −2 lnx
x+ 2
∣∣∣∣2
1
+
2∫
1
2
x (x+ 2)
dx = −1
2
ln 2 +
2∫
1
(
1
x
− 1
x+ 2
)
dx
= −1
2
ln 2 + (ln |x| − ln |x+ 2|)|21 = ln 3−
3
2
ln 2
Vậy I = I1 + I2 = ln
4
3
− 1
6
+ ln 3− 3
2
ln 2 =
1
2
ln 2− 1
6
.
Câu 6 (1,0 điểm).
Đáy ABCD là hình thoi nên có diện tích SABCD =
1
2
AC.BD =
1
2
.2a.4a = 4a2.
Gọi H là trung điểm AB, tam giác SAB đều nên SH⊥AB.
Lại có (SAB)⊥(ABCD) suy ra SH⊥(ABCD).
2
Gọi O là giao điểm của AC và BD, ta có OA = a,OB = 2a⇒ AB = √OA2 +OB2 = a√5.
Tam giác SAB đều cạnh a
√
5 nên đường cao SH = a
√
5.
√
3
2
=
a
√
15
2
.
Do đó thể tích khối chóp S.ABCD là VS.ABCD =
1
3
.SABCD.SH =
1
3
.4a2.
a
√
15
2
=
2a3
√
15
3
.
A B
CD
S
H
K
I
O
Ta có AD||BC ⇒ AD||(SBC).
Do đó d (AD,SC) = d (AD, (SBC)) = d (A, (SBC)) = 2d (H, (SBC)).
Gọi K là hình chiếu của H trên BC, ta có BC⊥HK và BC⊥SH nên BC⊥(SHK).
Gọi I là hình chiếu của H trên SK, ta có HI⊥SK và HI⊥BC nên HI⊥(SBC).
Từ đó suy ra d (AD,SC) = 2d (H, (SBC)) = 2HI.
Ta có HK =
2S∆HBC
BC
=
S∆ABC
BC
=
SABCD
2BC
=
4a2
2a
√
5
=
2a√
5
.
Tam giác SHK vuông tại H nên HI =
HS.HK√
HS2 +HK2
=
2a
√
15√
91
.
Vậy d (AD,SC) = 2HI =
4a
√
15√
91
.
Câu 7 (1,0 điểm).
A
B C
H
M
A′
d1 d2
Gọi d1 : 2x− y + 5 = 0 và d2 : 7x− y + 15 = 0.
Tọa độ B là nghiệm của hệ
{
2x− y = −5
7x− y = −15 ⇔
{
x = −2
y = 1
⇒ B(−2; 1).
Gọi H là hình chiếu của A trên d1 ⇒ H (t; 2t+ 5)⇒ −−→AH = (t− 1; 2t+ 3).
Khi đó
−−→
AH.−→ud1 = 0⇔ t− 1 + 4t+ 6 = 0⇔ t = −1⇒ H(−1; 3).
Gọi A′ là điểm đối xứng với A qua d1 ⇒ A′(−3; 4).
Khi đó A′ ∈ BC ⇒ −−→uBC =
−−→
BA′ = (−1; 3)⇒ BC có phương trình
{
x = −2− t
y = 1 + 3t
.
Vì C ∈ BC ⇒ C(−2− t; 1 + 3t). Gọi M trung điểm AC ⇒M
(−t− 1
2
;
3t+ 3
2
)
.
Khi đó M ∈ d2 nên 7(−t− 1)− (3t+ 3) + 30 = 0⇔ t = 2⇒ C(−4; 7).
Ta có AB =
√
10;AC = 5
√
2;BC = 2
√
10⇒ tam giác ABC vuông tại B.
Vậy tam giác ABC có diện tích là S∆ABC = 10.
3
Câu 8 (1,0 điểm).
Tọa độ giao điểm M của d và (P ) là nghiệm hệ
3x+ 5y − z − 2 = 0x− 12
4
=
y − 9
3
=
z − 1
1
.
Giải hệ ta được tọa độ giao điểm của d và (P ) là M(0; 0;−2).
Mặt phẳng (P ) có vectơ pháp tuyến −−→n(P ) = (3; 5;−1).
Đường thẳng d có vectơ chỉ phương −→ud = (4; 3; 1).
Mặt phẳng (Q) chứa d nên qua M(0; 0;−2).
Hơn nữa (Q) vuông góc với (P ) nên nhận
[−−→n(P ),−→ud] = (8;−7;−11) làm vectơ pháp tuyến.
Vậy (Q) có phương trình 8x− 7y − 11z − 22 = 0.
Câu 9 (0,5 điểm).
Phép thử là lấy cùng lúc từ mỗi hộp một cây viết nên |Ω| = C111.C115 = 165.
Gọi A là biến cố "hai cây viết được lấy ra có cùng màu", ta có |ΩA| = C15 .C17 + C16 .C18 = 83.
Vậy xác suất cần tìm là P (A) =
|ΩA|
|Ω| =
83
165
.
Câu 10 (1,0 điểm).
Trước hết chứng minh rằng với mọi số thực dương x ta có 14x+ 2 > 25x2 − 9x4 (∗).
Thật vậy (∗)⇔ 9x4 − 25x2 + 14x+ 2 > 0⇔ (x− 1)2 (9x2 + 18x+ 2) > 0 (luôn đúng).
Dấu bằng của (∗) xảy ra khi x = 1.
Thay x bởi a, b, c được 14a+ 2 > 25a2 − 9a4; 14b+ 2 > 25b2 − 9b4; 14c+ 2 > 25c2 − 9c4.
Từ đó suy ra 14(a+ b+ c) > 25 (a2 + b2 + c2)− 9 (a4 + b4 + c4)⇔ a+ b+ c > 3.
Do đó theo bất đẳng thức Cauchy − Schawrz dạng Engel ta có :
P =
a2
b+ 2c
+
b2
c+ 2a
+
c2
a+ 2b
> (a+ b+ c)
2
3 (a+ b+ c)
=
a+ b+ c
3
> 1
Dấu bằng xảy ra khi a = b = c = 1.
Vậy giá trị nhỏ nhất của P bằng 1 khi a = b = c = 1.
——— Hết ———
4