Đề thi tham khảo kiểm tra học kỳ II môn toán lớp 9 năm học 2015 - 2016

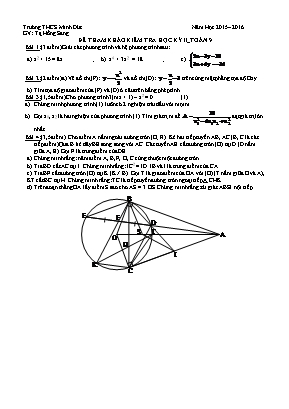
Trường THCS Minh Đức	Năm Học 2015– 2016
GV: Tạ Hồng Sang
ĐỀ THAM KHẢO KIỂM TRA HỌC KỲ II_TOÁN 9
(3 điểm) Giải các phương trình và hệ phương trình sau:
x2 + 15 = 8x	; b) x4 + 3x2 = 18	;	c) 
(2 điểm) a) Vẽ đồ thị (P): và đồ thị (D): trên cùng mặt phẳng tọa độ Oxy.
Tìm tọa độ giao điểm của (P) và (D) ở câu trên bằng phép tính.
(1,5 điểm) Cho phương trình 3(mx + 1) – x2 = 0	(1)
Chứng minh phương trình (1) luôn có 2 nghiệm trái dấu với mọi m
Gọi x1, x2 là hai nghiệm của phương trình (1). Tìm giá trị m để đạt giá trị lớn nhất
(3,5 điểm) Cho điểm A nằm ngoài đường tròn (O; R). Kẻ hai tiếp tuyến AB, AC (B, C là các tiếp điểm) Qua B kẻ dây BE song song với AC. Cát tuyến AE cắt đường tròn (O) tại D (D nằm giữa A, E). Gọi F là trung điểm của DE
Chứng minh rằng: năm điểm A, B, F, O, C cùng thuộc một đường tròn.
Tia BD cắt AC tại I. Chứng minh rằng: IC2 = ID. IB và I là trung điểm của CA. 	
Tia BF cắt đường tròn (O) tại K (K ≠ B). Gọi T là giao điểm của OA với (O) (T nằm giữa O và A), KT cắt BC tại H. Chứng minh rằng: TC là tiếp tuyến đường tròn ngoại tiếp rCHK.	
Trên đoạn thẳng OA lấy điểm S sao cho AS = 3.OS. Chứng minh rằng: tứ giác ABSI nội tiếp.
Gợi ý và đáp án
(3 điểm) Giải các phương trình và hệ phương trình sau:
x2 + 15 = 8x Û x2 – 8x + 15 =	0 . r’ = b’2 – ac = 16 – 15 = 1 	(0,25đ + 0,25đ)
Þ x1 = 5 ; x2 = 3	(0,25đ + 0,25đ)
	x4 + 3x2 = 18	Û x4 + 3x2 – 18 = 0. Đặt t = x2 > 0 Pt thành t2 + 3t – 18 = 0	(0,25đ)
r = b2 – 4ac = 81 > 0 Þ 	(0,25đ)
(nhận)	; (loại)	(0,25đ + 0,25đ)
	t = 3 Þ x2 = 3 Û 	(0,25đ)	
	(0,25đ x 3)
a) BGT đúng (0,25đ x 2) ;	Vẽ đúng (0,25đ x 2) 
Û x2 + x – 6 = 0 Û  Û x1 = 2 ; x2 = – 3(0,25đ x 3)
Þ (2 ; –2) ; ( –3 ; –4,5) là các giao điểm cần tìm 	(0,25đ)
 a) a = –1 ; c = 3 là hai số luôn trái dấu "m và P = ac = – 3 
Þ Pt luôn có hai nghiệm trái dấu	(0,25đ x 3)
b) S = 3m ; P = – 3 Þ A ≤ 1	(0,25đ x 3)
Cmđ: năm điểm A, B, F, O, C thuộc một đường tròn đường kính OA 	(0,25đ x 4)
Cmđ: rCBIrDCI Þ IC2 = ID. IB và cmđ IA2 = ID. IB Þ I là trung điểm của CA.(0,25đ x 4)
Cmđ: Þ CT là tiếp tuyến đường tròn ngoại tiếp rCHK (định lý đảo về tiếp tuyến). 	(0,25đ x 3)
Cmđ S là tâm đường tròn ngoại tiếp rBIC 
Áp dụng góc ngoài bằng góc đối trong Þ tứ giác ABSI nội tiếp. 	(0,25đ x 3)