Đề thi olympic lớp 8 năm học 2013 - 2014 môn thi : Toán thời gian làm bài : 120 phút (không kể thời gian giao đề )

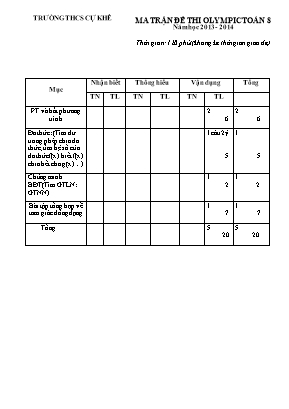
 TRƯỜNG THCS CỰ KHÊ
MA TRẬN ĐỀ THI OLYMPIC TOÁN 8
Năm học 2013 - 2014
Thời gian: 120 phút (không kể thời gian giao đề)
Mục
Nhận biết
Thông hiểu
Vận dụng
Tổng
TN
TL
TN
TL
TN
TL
PT và bất phương trình
2
 6
2
 6
Đa thức: (Tìm dư trong phép chia đa thức; tìm hệ số của đa thức f(x) biết f(x) chia hết cho g(x))
1câu 2ý
 5
1
 5
Chứng minh BĐT(Tìm GTLN: GTNN)
1
 2
1	
 2
Bài tập tổng hợp về tam giác đồng dạng
1	
 7
1
 7
 Tổng
5
 20
5
 20
phßng Gi¸o dôc & §µo t¹o
§Ò thi olympic líp 8
N¨m häc 2013 - 2014
M«n thi : To¸n
Thêi gian lµm bµi : 120 phót 
(kh«ng kÓ thêi gian giao ®Ò )
Câu 1 ( 6 điểm ) 
Giải phương trình: 
a, 
b, 
 2. Chứng minh rằng với 4 số bất kỳ a, b, x, y ta có
(a2 + b2)(x2 + y2) (ax + by)2
Câu 2 ( 5 điểm ) 
1. Chứng minh rằng: x3m+1 + x3n+2 + 1 chia hết cho x2 + x + 1 với mọi số tự 
 nhiên m,n.
 	2. tìm caùc soá nguyeân a vaø b ñeå ña thöùc A(x) = chia heát cho ña 
 thöùc 
Câu 3 ( 2 điểm ) 
	a)Chứng minh bất đẳng thức : (với x và y cùng dấu) 
b)Tìm giá trị nhỏ nhất của biểu thức P = (với )
Câu 4 ( 7 điểm )
	Cho tam giác ABC vuông tại A. Lấy một điểm M bất kỳ trên cạnh AC. Từ C vẽ một đường thẳng vuông góc với tia BM, đường thẳng này cắt tia BM tại D, cắt tia BA tại E.
 a) Chứng minh: EA.EB = ED.EC và 
 b) Cho và . Tính SEBC?
 c) Chứng minh rằng khi điểm M di chuyển trên cạnh AC thì tổng BM.BD + CM.CA có giá trị không đổi.
 d) Kẻ. Gọi P, Q lần lượt là trung điểm của các đoạn thẳng BH, DH. Chứng minh .
__________________________________________________________
TRƯỜNG THCS CỰ KHÊ
H­íng dÉn chÊm thi olympic
N¨m häc 2013 - 2014
M«n thi : To¸n Líp 8
Câu
Nội dung
Điểm
Câu 1
(6 điểm)
1. a, (1)
+ Nêu : (1) x =1 (thỏa mãn điều kiện ).
+ Nêu : (1) 
 (cả hai đều không nhỏ hơn 1, nên bị loại)
Vậy: Phương trình (1) có một nghiệm duy nhất là .
 b, 
 2. Ta có (a2 + b2)(x2 + y2) (ax + by)2
	 a2x2 + a2y2 + b2x2 + b2y2 a2x2 + 2axby + b2y2	
	 a2y2 - 2axby + b2x2 0 (ay - bx)2 0	
Vì bất đẳng thức cuối cùng là bất đẳng thức đúng nên bất đẳng thức phải chứng minh là bất đẳng thức đúng.	
Dấu “=” xảy ra khi và chỉ khi ay - bx = 0 hay 	
0,5đ.
0,5đ.
0,5đ.
0,5đ.
0,5đ.
0,5đ.
0,5đ.
0,5đ.
0,5đ.
0,5đ.
0,5đ.
0,5đ.
Câu 2
(5 điểm)
1. Ta có x3m+1 + x3n+2 + 1 = x3m+1 - x + x3n+2 - x2 + x2 + x + 1	
	= x(x3m - 1) + x2(x3n - 1) + (x2 + x + 1)	
Ta thấy x3m - 1 và x3n - 1 chia hết cho x3 - 1 do đó chia hết cho x2 + x + 1
x3m+1 + x3n+2 + 1 chia hết cho x2 + x + 1
2. Ta coù: A(x) =B(x).(x2-1) + ( a – 3)x + b + 4
Ñeå thì 
1,0đ.
0,5đ.
0,5đ.
0,5đ.
1,5đ.
1,0đ.
Câu 3
(2 điểm)
Vì x, y cùng dấu nên xy > 0, do đó (*) 
(**). Bất đẳng thức (**) luôn đúng, suy ra bđt (*) đúng (đpcm)
 Đặt 	
 Biểu thức đã cho trà thành P = t2 – 3t + 3 
	P = t2 – 2t – t + 2 + 1 = t(t – 2) – (t – 2) + 1 = (t – 2)(t – 1) + 1	
- Nêu x; y cùng dấu, theo c/m câu a) suy ra t 2. t – 2 0 ; t – 1 > 0 . Đẳng thức xảy ra khi và chỉ khi t = 2 
x = y (1) 
- Nêu x; y trái dấu thì và t < 0 t – 1 < 0 và t – 2 < 0 
 > 0 P > 1 	(2)	
- Từ (1) và (2) suy ra: Với mọi x 0 ; y 0 thì luôn có P 1. Đẳng thức xảy ra khi và chỉ khi x = y. Vậy giá trị nhỏ nhất của biểu thức P là Pm=1 khi x = y
0,25đ.
0,25đ.
0,25đ
(0,25đ)	(0,25đ)	
(0,25đ)	(0,25đ)	(0,25đ)	.
Câu 4
(7 điểm)
Câu a: 2 điểm
* Vẽ hình + ghi gt và kl 
* Chứng minh EA.EB = ED.EC	
- Chứng minh EBD đồng dạng với ECA (gg)	
- Từ đó suy ra 	
* Chứng minh 	
- Chứng minh EAD đồng dạng với ECB (cgc)	
- Suy ra 	
Câu b: 1,5 điểm
- Từ = 120o = 60o = 30o	
- XÐt EDB vuông Tại D có = 30o
	 ED = EB 	
- Lý luận cho Từ đó SECB = 144 cm2	
Câu c: 1,5 điểm
- Vẽ MI ^BC (I thuộc BC)
- Chứng minh BMI đồng dạng với BCD (gg) => BM.BD = BC.BI 
- Chứng minh IMCđồng dạng với ABC (gg) => CM.CA = CI.BC
- Chứng minh BM.BD + CM.CA = BC2 có giá trị không đổi	 
(Cách 2: Có thể biến đổi BM.BD + CM.CA = AB2 + AC2 = BC2 )
Câu d: 2 điểm
- Chứng minh BHD đồng dạng với DHC (gg) 	
- Chứng minh DPB đồng dạng với CQD (cgc)
0,5đ.
0,5đ.
0,5đ.
.
0,5đ.
0,5đ.
0,5đ.
0,5đ.
0,5đ
0,5đ.
0,5đ.
0,5 đ
0,5đ.
1.0đ.
Ký duyệt của tổ CM Người ra đề , đáp án 
Trịnh Văn Đông	 Nguyễn Đức Anh
 Ban giám hiệu nhà trường
 PHT: Vũ Thị Hồng Thắm