Đề thi Kiểm tra tiết 25 năm học 2015 - 2016 môn: Hình học lớp: 8 thời gian làm bài 45 phút

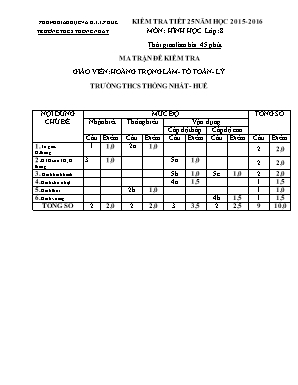
 PHÒNG GIÁO DỤC VÀ Đ.T.T.P HUẾ KIỂM TRA TIẾT 25 NĂM HỌC 2015- 2016
 TRƯỜNG THCS THỐNG NHẤT MÔN: HÌNH HỌC Lớp: 8 
 Thời gian làm bài 45 phút
 MA TRẬN ĐỀ KIỂM TRA
GIÁO VIÊN: HOÀNG TRỌNG LÂM- TỔ TOÁN- LÝ
TRƯỜNG THCS THỐNG NHẤT- HUẾ
NỘI DUNG CHỦ ĐỀ
MỨC ĐỘ
TỔNG SỐ
Nhận biết
Thông hiểu
Vận dụng
Cấp độ thấp
Cấp độ cao
Câu
Điểm
Câu
Điểm
Câu
Điểm
Câu
Điểm
Câu
Điểm
1. Tứ giác 
H.thang
1
1,0
2a
1,0
2
2,0
2 .ĐTB của TG, H thang
3
1,0
5a
1,0
2
2,0
3. Hình bình hành
5b
1,0
5c
1,0
2
2,0
4. Hình chữ nhật
4a
1,5
1
1,5
5. Hình thoi
2b
1,0
1
1,0
6. Hình vuông
4b
1,5
1
1,5
TỔNG SỐ
2
2,0
2
2,0
3
3,5
2
2,5
9
10,0
 PHÒNG GIÁO DỤC VÀ Đ.T.T.P HUẾ KIỂM TRA TIẾT 25 NĂM HỌC 2013- 2014
 TRƯỜNG THCS THỐNG NHẤT MÔN: HÌNH HỌC Lớp: 8 
 Thời gian làm bài 45 phút
ĐỀ KIỂM TRA SỐ 
Câu 1: ( 1đ) Tìm x trong hình vẽ sau 
Câu 2: ( 2,0đ) a) Hình thang ABCD có AB // CD, AB= 4cm , đường trung bình EF = 8cm. Hỏi DC = ?cm
 b/ Hình thoi ABCD có hai đường chéo là AC = 10cm và 
BD= 12cm thì độ dài một cạnh bằng bao nhiêu ? 
Câu 3 :(1đ) Tam giác vuông có cạnh huyền bằng 12cm. Hỏi trung tuyến ứng với cạnh huyền bằng bao nhiêu?
Câu 4 :(3.0 đ) Cho tam giác ABC vuông tại A. Điểm D thuộc cạnh BC. Gọi E và F lần lượt là hình chiếu của D trên AC, AB. 
a) Chứng minh AD = EF
b) Xác định điểm D trên cạnh BC để tứ giác AEDF là hình vuông
 Câu 5 :(3.0 đ) Cho hình bình hành ABCD. Từ A kẽ đường thẳng vuông góc với BD tại E vàcắt DC tại M. Từ C kẽ đường thẳng vuông góc với BD tại F và cắt AB tại N. Gọi I là trung điểm của EF.
	a) Chứng minh AE = CF
	b) Chứng minh AF = CE
	c) Chứng minh M và N đối xứng nhau qua I
PHÒNG GIÁO DỤC VÀ Đ.T.T.P HUẾ KIỂM TRA TIẾT 25 NĂM HỌC 2013- 2014
 TRƯỜNG THCS THỐNG NHẤT Môn: HÌNH HỌC Lớp: 8 
ĐÁP ÁN VÀ THANG ĐIỂM ĐỀ KIỂM TRA SỐ:
( Đáp án này gồm 03 trang )
BÀI
CÂU
NỘI DUNG
ĐIỂM
1
1,0
Trong tứ giác ABCD ta có: 
A + B + C+ D = 3600( Địnhlý )
x + 1100 + 900 + 850= 3600
x + 2850 = 3600
	x	= 3600 - 2850
 x = 750
 Vậy: x = 750
0,25
0,25
0,25
0,25
2
2,0
a)
b)
EF là đường trung bình của hình thang ABCD có 
AB// CD, nên:
EF= AB+CD2
Mà AB= 4cm, EF= 8cm, nên:
8= 4+CD2⟺ 4+ CD= 16
 ⟺CD = 12 ( cm )
Vậy: CD = 12 cm
 Gọi O là giao điểm hai đường chéo AC và BD, theo tính chất hình thoi ta có:
OB= 12 BD 
 = 12∙10 
 = 5( cm )
OC= 12∙AC
 = 12∙12
 = 6 ( cm)
Ta có: AC ⊥BD; ( Tính chất hai đường chéo hình thoi )
∆BOC vuông tại O nên:BC2= OB2+OC2
 = 52+ 62
 = 25 + 36
 = 61
 Suy ra: BC = 61 ( cm)
Vậy: Độ dài cạnh hình thoi bằng 61 cm
0,5
0,5
0,25
0,25
0,5
3
1,0
∆ABC vuông tại A nên: AM= 12 BC( Tính chất đường trung tuyến trong tam giác vuông )
 Suy ra: AM = 12∙12
 = 6 ( cm )
0,25
0,75
4
3,0
 A
 F	E
B D C
* Vẽ hình đúng, chính xác
a) Tứ giác AEDF có ba góc vuông là hình chữ nhật.
 Suy ra được hai đường chéo bằng nhau: AD = EF
b) Nêu được ý : 
 * Để tứ giác AEDF là hình vuông thì đường chéo AD đồng thời là phân giác của góc A
 * Do đó D là giao điểm của đường phân giác góc A với cạnh BC
0,5
0,5
0,5
1,0
0.5
5
3,0
 A	N	B
 E I	F
 D M C
0,25
* Vẽ hình đúng, chính xác
a) Nêu được DEAD và DFCB vuông và có :
 AD = BC ( tính chất hình bình hành)
 ADE= CBF ( So le trong; AD // BC)
 Do đó chúng bằng nhau (cạnh huyền- góc nhọn) 
 Suy ra được AE = CF
b) Nêu được AECF có AE // CF (cùng ^ BD)
 và AE = CF (theo câu a)
 Nên tứ giác AECF là hình bình hành 
 suy ra AF = CE 
c) * Vì AECF là hình bình hành, mà I là trung điểm của đường chéo EF nên I cũng là trung điểm của đường chéo AC
 * Tứ giác ANCM có các cạnh đối song song là hình bình hành 
 * Mà I là trung điểm của đường chéo AC nên I cũng là trung điểm của đường chéo MN. Do đó M và N đối xứng nhau qua I 
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,5
0,25
0,25