Đề thi học kỳ II môn toán 12

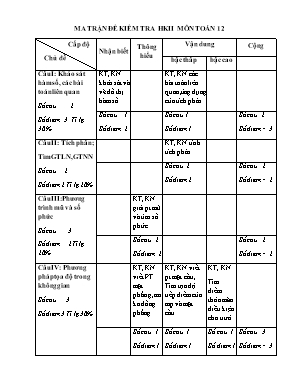
MA TRẬN ĐỀ KIỂM TRA HKII MÔN TOÁN 12
 Cấp độ
 Chủ đề
Nhận biết
Thông hiểu
Vận dung
Cộng
bậc thấp
bậc cao
Câu I: Khảo sát hàm số, các bài toán liên quan
Số câu 2
Số điểm 3 Tỉ lệ 30 %
KT, KN khảo sát và vẽ đồ thị hàm số
KT, KN các bài toán liên quan,ứng dụng của tích phân
Số câu 1
Số điểm 2
Số câu 1
Số điểm 1
Số câu 2
Số điểm= 3
Câu II: Tích phân;
Tìm GTLN,GTNN
Số câu 2
Số điểm 2 Tỉ lệ 20%
KT, KN tính tích phân
Số câu 2
Số điểm 2
Số câu 2
Số điểm= 2
Câu III:Phương trình mũ và số phức
Số câu 3
Số điểm 2Tỉ lệ 20%
KT, KN giải pt mũ và tìm số phức.
Số câu 2
Số điểm 2
Số câu 2
Số điểm= 2
Câu IV: Phương pháp tọa độ trong không gian
Số câu 3
Số điểm 3 Tỉ lệ 30%
KT, KN viết PT mặt phẳng,cm ko đồng phẳng.
KT, KN viết pt mặt cầu, Tìm tọa độ tiếp điểm của mp và mặt cầu
KT, KN
Tìm điểm thỏa mãn điều kiện cho trướ
Số câu 1
Số điểm 1
Số câu 1
Số điểm 1
Số câu 1
Số điểm 1
Số câu 3
Số điểm= 3
Tổng số câu
1
3
4
1
Số câu 9
Tổng số điểm
2
3
	4
1.
Số điểm=10.0
ĐỀ THI HỌC KỲ II MÔN TOÁN 12
Câu 1: (3 điểm)
 Cho hàm số: (c)
 a)Khảo sát và vẽ đồ thị hàm số (c)
 b)Tính diện tích hình phẳng giới hạn bởi đồ thị (c),trục hoành ,
 các đường thẳng x=-1;x=1.
Câu 2 : (2 điểm)
 a)Tìm GTLN,GTNN cúa hàm số: trên [1;3]
 b)Tính: 
Câu 3 :(2 điểm)
 a) Giải phương trình sau: 
 b) Tìm phần thực phần ảo của số phức sau:
Câu 4 : (3 điểm)
 Trong không gian (Oxyz) cho A(-3;1;1); B(1;-2;3); C(O;1;2);D(-1;1;2)
 a)Viết phương trình (ABC)từ đó CMR : A,B,C,D là 4 đỉnh của hình tứ diện.
 b)Viết phương trình mặt cầu (S) có tâm D và tiếp xúc mặt phẳng(ABC).
 Tìm tiếp điểm.
 c) Tìm tọa độ điểm M thuộc đường thẳng ∆: 
 sao cho độ dài đường gấp khúc BMC ngắn nhất.
ĐÁP ÁN VÀ THANG ĐIỂM
Câu
Nội dung
Điểm
Câu 1a
(2đ)
*Tập xác định: R
0.5
*Sự biến thiên:
Bảng biến thiên:
x
- 1 3 +
Y’
 + 0 - 0 +
y
 + 
 4
-	 0
0.5
Hàm số đồng biến trên các khoảng(- ;1) và(3; +)
Hàm số nghịch biến trên khoảng (1;3)
Hàm số đạt cực đại tại x=1
Hàm số đạt cực tiểu tại x=3
0,5
*Vẽ đồ thị
0,5
Câu 1b
(1đ)
0,5
==(đvdt)
0,5
Câu 2a
(1đ)
Hàm số liên tục trên[1,3]
0,25
 [1;3]
0,25
0,25
Kết luận:
0,25
Câu 2b
(1đ)
Đặt :
0,5
0,5
Câu 3a
(1đ)
x=1
1
Câu 3b
(1đ)
0,5
 =
Phần thực:a= 
Phần ảo:b= 
0,5
Câu 4 a (1đ)
0,5đ
Pt(ABC):-3(x+3)+2(y-1)+9(z-1)=0 -3x+2y+9z-20=0 (1)
0,25
Thay tọa độ điểm D vào pt(1) ko thỏa mãn KL
0,25
Câu 4b
(1đ)
R=
0,25
PT mặt cầu:
0,25
Gọi d là đường thẳng đi qua D và vuông (ABC)
0,25
Xét pt:-3(-1-3t)+2(1`+2t)+9(2+9t)-20=0 t= 
 Tiếp điểm là H( ; ; )
0,25
Câu 4c
(1đ)
Từ gt ⟹∆:x=1+ty=2-tz=2t . ∀M∈∆⟹M(1+t;2-t;2t)
⟹BMt;4-t;2t-3; CM(1+t;1-t;2t-2)
⟹BM2=t2+(4-t)2+(2t-3)2=6t2-20t+25
 CM2=(1+t)2+(1-t)2+(2t-2)2=6t2-8t+6.
Độ dài đường gấp khúc BMC=BM+CM
= 6t2-20t+25+6t2-8t+6 
 =6(t-106)2+5036+(t-46)2+2036. 
0,5
 y 
 B1
 M0 M1 x
 O 
 C1 
Trên Oxyz, gọi M1(t;0;0)∈Ox.
B1106;526;0∈(Oxy) và ở trên Ox. C146;-256;0∈(Oxy) và ở dưới Ox.
⟹B1M1=(t-106)2+5036. ⟹C1M1=(t-46)2+2036
Khi đó BM+CM=6B1M1+C1M1 = 6.100+210006 = 106+210006.
Dấu = xảy ra ⟺ B1,M1,C1 thẳng hàng ⟺B1M1 cùng phương với B1C1
Mà B1M1(t-106;-526;0) ; B1C1(-1;-20-506;0).
Do đó : t-106-1=-526-20-506 ⟺ t-106=-5050+20
Vậy t= 106-5050+20 = t0. Vậy M(1+t0; 2-t0;2t0) 
Với t0=106-5050+20=450+10206(50+20).
0,5