Đề thi học kì II - Năm học 2015 - 2016 môn: Toán - khối 11 thời gian: 90 phút

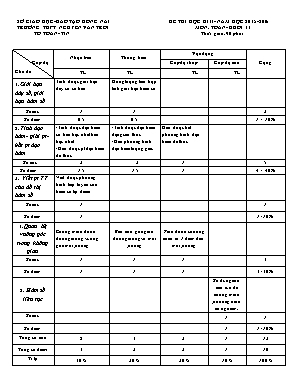
SỞ GIÁO DỤC- ĐÀO TẠO ĐỒNG NAI
TRƯỜNG THPT NGUYỄN VĂN TRỖI
 TỔ TOÁN- TIN
 ĐỀ THI HỌC KÌ II- NĂM HỌC 2015-2016
 MÔN: TOÁN- KHỐI 11
 Thời gian: 90 phút
 Cấp độ
Chủ đề
Nhận biết
Thông hiểu
Vận dụng
Cộng
Cấp độ thấp
Cấp độ cao
TL
TL
TL
TL
1. Giới hạn dãy số, giới hạn hàm số
Tính được giới hạn dãy số cơ bản
Dùng lượng liên hợp tính giới hạn hàm số
Số câu
1
1
2
Số điểm
0,5
0,5
1 = 10%
2. Tính đạo hàm- giải pt-bất pt đạo hàm
-Tính được đạo hàm cơ bản bậc nhất trên bậc nhất
-Giải được pt đạo hàm đa thức
-Tính được đạo hàm dạng căn thức
-Giải phương trình đạo hàm lượng giác
Giải được bất phương trình đạo hàm đa thức 
 Số câu
2
 2
1
5
 Số điểm
1,5
 1,5
1
4 = 40%
3. Viết pt TT của đồ thị hàm số
Viết được phương trình tiếp tuyến của hàm số tại điểm
Số câu
1
1
 Số điểm
1
1=10%
4. Quan hệ vuông góc trong không gian
Chứng minh được đường thẳng vuông góc mặt phẳng
Biết tính góc giữa đường thẳng và mặt phẳng
Tính được khoảng cách từ 1 điểm đến mặt phẳng
Số câu
1
1
1
3
Số điểm
1
1
1
3=30%
5. Hàm số liên tục
Sử dụng tính liên tục để chứng minh phương trình có nghiệm.
Số câu
1
1
Số điểm
1
1=10%
Tổng số câu
5
4
2
1
12
Tổng số điểm
4
3
2
1
10
Tỉ lệ
40%
30%
20%
10%
100%
SỞ GIÁO DỤC- ĐÀO TẠO ĐỒNG NAI
TRƯỜNG THPT NGUYỄN VĂN TRỖI
 TỔ TOÁN- TIN
 ĐỀ THI HỌC KÌ II- NĂM HỌC 2015-2016
 MÔN: TOÁN- KHỐI 11
 Thời gian: 90 phút
Câu I(1 điểm). Tìm các giới hạn sau:
1) 	2) 
Câu II(1 điểm). Tính đạo hàm của các hàm số sau:
1) 2) 
Câu III(2điểm). Giải phương trình y’ =0 biết :
	b) 
Câu IV(3điểm). Cho hình chóp S.ABCD có đáy ABCD hình vuông cạnh bằng a. Cạnh bên SA vuông góc mặt phẳng và .
	1) Chứng minh rằng BD vuông góc mặt phẳng (SAC).
	2) Tính góc hợp bởi đường thẳng SC với mặt phẳng (SAB).
	3) Tính khoảng cách SC và BD
Câu V(2điểm). Cho hàm số có đồ thị (C).
1) Giải phương trình 
	2) Viết phương trình tiếp tuyến với đồ thị (C) tại điểm có hoành độ 
Câu VI (1 điểm). Cho f(x) = ax2 + bx + c thoả mãn : 2a + 3b + 6c = 0.
Chứng minh rằng phương trình ax2 + bx + c = 0 có nghiệm trong khoảng (0;1).
-------------HẾT------------
Họ và tên:..................................................................Số báo danh:...........................................
ĐÁP ÁN VÀ THANG ĐIỂM THI HỌC KÌ II- MÔN TOÁN 11 NĂM HỌC 2015-2016
CÂU
Ý
NỘI DUNG
ĐIỂM
I
(1đ)
1(0,5đ)
 = - 2 
 0,25
0,25
2(0,5đ)
0,25
0,25
II
(1đ)
a
0,25
 0,25
b
III
(2 đ)
1(1 đ)
Cho 
 0,25
0,25
 0,5
2(0,5đ)
0,5
0,5
IV
(3đ)
1(1đ)
BD ^ AC
 BD ^ SA	
Þ BD ^ (SAC)	
0,5
0,25
0,25
2(1đ)
CB ^ (SAB) Þ BS là hình chiếu của SC trên (SAB)
Þ 
Kết luận:
0,5
0,25
0,25
3(1đ)
Vì BD ^ (SAC) tại tâm 0 nên từ 0 kẻ OH ^ SC do đó OH ^ BD
Vậy OH là đoạn vuông góc chung của BD và SC.
Tam giac HCO đồng dạng ACS (g.g)
Nên 
0,25
0,25
0,25
0,25
Va
(2đ)
1(1đ)
 Þ 
0,5
0,25
0,25
2(1đ)
Tại Þ 
Hệ số góc của TT: 
Phương trình tiếp tuyến là 
0,25
0,5
0,25
VI
(1 đ)
0,25
0,25
0,25
0,25