Đề ôn tập môn Toán Lớp 8 - Chủ đề: Tam giác đồng dạng

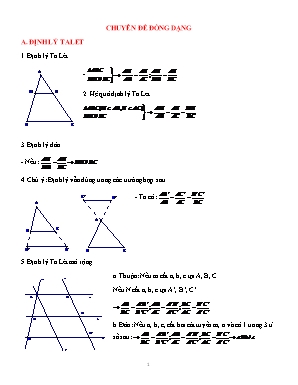
CHUYÊN ĐỀ ĐỒNG DẠNG
A. ĐỊNH LÝ TALET	
1. Định lý Ta Lét
- 
2. Hệ quả định lý Ta Let
3. Định lý đảo	
- Nếu: 
4. Chú ý: Định lý vẫn đúng trong các trường hợp sau
- Ta có: 
5. Định lý Ta Lét mở rộng
a. Thuận: Nếu m cắt a, b, c tại A, B, C
Nếu N cắt a, b, c tại A’, B’, C’
b. Đảo: Nếu a, b, c, cắt hai cát tuyến m, n và có 1 trong 3 tỉ số sau: 
*) Hệ quả: ( các đường thẳng đồng quy cắt hai đường thẳng song song )
1. Hệ quả 1: Nhiều đường thẳng đồng quy định ra trên hai đường thẳng song song những đoạn thẳng tương ứng tỷ lệ
2. Hệ quả 2: Nhiều đường thẳng không song song định ra trên hai đường thẳng song song các đoạn thẳng tương ứng tỷ lệ thì chúng đồng quy tại 1 điểm
- d’, d’’, d’’’ không song song cắt hai đường thẳng song song a và b tại A, B, C và A’, B’,C’
Và thảo mãn: 
Bài 1: Cho hình bình hành ABCD và điểm E thuộc đoạn BD. Gọi M, N lần lượt là giao điểm của BC, BD với AE. Qua C kẻ đường thẳng song song với BD cắt MN tại F. Chứng minh rằng
a. 
b. 
c. 
Lời giải
a. 
Ta có: ( Các đường thẳng song song )
b. 
Ta có: 
Chia cả hai vế cho AE, ta được: 
c. Ta có: 
Từ (1)(2) 
Bài 2: Cho hình thang ABCD có AB // CD, AB < CD. Kẻ đường thẳng qua A song song với BC cắt BD ở E, đường thẳng qua B song song với AD cắt AC ở F. GỌi M, N lần lượt là giao điểm của FE với AD, B. Chứng minh rằng:
a. EM = FN
b. 
Lời giải
Ta phải đi chứng minh FE // AB // CD Hay 
- Ta có: ABQD và ABCP là hình bình hành nên AB = DQ = CP 
+) 
a. Ta có: 
Hoặc: 
b. 
Bài 3: Cho tam giác ABC. Một đường thẳng song song với BC cắt các cạnh AB, AC tại D và E. Qua C kẻ đường thẳng song song với AB cắt DE tại F. Gọi H là giao điểm của AC với BF. Đường thẳng qua H song song với BC tại I. Chứng minh rằng
a. 
b. 
c. 
Lời giải
a. 
b. 
c. 
Bài 4: Cho hình thang ABCD ( AB // CD ). Gọi M là trung điểm của CD, gọi I là giao điểm của AM với BD, K là giao điểm của BM với AC, đường thẳng IK cắt AD, BC lần lượt tại E và F. Chứng minh rằng:
a. IK // AB
b. EI = IK = KF
Lời giải
a. 
b. Có : 
Bài 5: Cho tam giác ABC, gọi D là điểm đối xứng với A qua B, E là điểm đối xứng với B qua C và F là điểm đối xứng với C qua A. Chứng minh rằng: có cùng trọng tâm
Lời giải
- Dựa vào tâm đối xứng của hình bình hành
- Hướng dẫn: G là trọng tâm là hình bình hành
Giải
Gọi M, N, P lần lượt là trung điểm của BC, DE, AB
 là đường trung bình của 
Là hình bình hành là trung điểm NP
+) MN là đường trung bình của 
Theo định lý Ta Lét: là trọng tâm của hai tam giác. 
Bài 6: Cho hình thang ABCD ( AB // CD, AB < CD ). AC cắt BD tại M. Kẻ qua M đường thẳng song song với AB cắt AD, BC lần lượt tại I và K
a. Chứng minh rằng: MI = MK
b. Kẻ Bx // AD, Bx cắt AC, CD tại E, F
Kẻ Ay // BC, Ay cắt BD, CD tại P, Q. Chứng minh rằng: DE // IK
c. Biết AB = a, CD = b. Tính IK theo a và b
Lời giải
a. Xét ( Hệ quả TaLet) (1)
- Tương tự ta có: 
Lại có: ( TaLet mở rộng ) (3) 
Từ (1)(2)(3) 
b. Ta đi chứng minh: 
Thật vậy: 
 là các hình bình hành 
Từ (4)(5)(6) (Ta Lét đảo )
c. Ta có: IK = 2 MI = 2 MK
Xét 
Xét 
Từ (1)(2) 
Bài 7: Cho hình hình bình ABCD, đường thẳng qua A cắt BD, CD, BC lần lượt tại E, I, K. CMR:
a. 
b. 
c. DI. BK không đổi
Lời giải
a. 
b. 
Ta có: 
c. Ta cần chứng minh: 
Chứng minh: Xét 
Xét 
Từ (1)(2) ( không đổi )
Hoặc cách khác:
 ( không đổi )
Bài 8: Cho Tứ giác ABCD, đường thẳng qua A song song với BC cắt BD ở E. Đường thẳng qua B song song với AD cắt AC ở G
a. Chứng minh rằng: EG // CD
b. Giả sử AB // CD. Chứng minh rằng: 
Lời giải
a. Hướng dẫn: 
 ( TaLet đảo )
b. Hướng dẫn: Giải: 
Từ (1)(2)(3) 
BÌ TẬP TỰ LUYỆN: Cho tam giác ABC vuông tại A, có: AB = a, AC = b. Vẽ ra phía ngoài tam giác đó các tam giác vuông cân ABD cân ở B và tam giác ACF vuông cân ở C. Gọi H là giao điểm của AB và CD, K là giao điểm của AC và BF. Chứng minh rằng
a. AH = AK
b. 
B. TÍNH CHẤT ĐƯỜNG PHÂN GIÁC
1. Định lý: Trong tam giác, đường phân giác cảu một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy
2. Chú ý: Định lý trên vẫn đúng đối với tia phân giác ngoài của tam giác
3. Chú ý 2: Nếu D thuộc BC mà: là phân giác 
4. Chú ý tính hất của tỉ lệ thức: 
Bài 1: Cho hình bình hành ABCD có AB > CD. Phân giác trong các góc BAD cắt BD tại M. Phân giác trong góc ADC cắt AC tại N. Chứng minh rằng: MN // AD
Lời giải
- Ta có: 
Lại có: 
Từ (1)(2) ( Ta Lét đảo ) 
Bài 2: Cho tam giác ABC, AB < AC, phân giác trong AD, M là trung điểm của BC. Đường thẳng qua M và song song với AD cắt AB, AC lần lượt tại P và Q. Chứng minh rằng: BP = CQ
Lời giải
*) Chú ý: Nếu mà: là phân giác góc BAC 
a. Cách 1: 
b. Cách 2: 
Bài 3: Khó: Cho tam giác vuông ABC vuông tại A có trọng tâm G, phân giác trong BD, biết . Tính 
Lời giải
Lời giải
Gọi M, E lần lượt là trung điểm của BC và AG
 cân tại E
Mặt khác, tam giác ABC vuông tại A, có AM = MB = MC 
 cân tại M
- Có: 
Vậy tam giác ABM là tam giác đều 
Bài 4: Khó: Cho tam giác ABC ( AB < AC ), các phân giác BD, CE
a. Đường thẳng qua D và song song với BC cắt AB ở K. Chứng minh E nằm giữa B và K
b. Gọi M là giao điểm của DE và CB. Chứng minh rằng: CD > DE > BE
Lời giải
a. E nằm giữa B và K 
Ta có: BD là phân giác góc B
Lại có: 
 nằm giữa B và K
b. Có: 
Lại có E nằm giữa K và B ( cạnh đối diện với góc lớn hơn )
+) Có: 
Bài 5: Cho tam giác ABC kẻ phân giác trong và phân giác ngoài của góc B cắt AC ở I và D. Từ I và D kẻ đường thẳng song song với BC cắt AB ở M và N
a. Tính AB và MN, biết: MI = 12cm, BC = 20cm
b. Từ C kẻ đường thẳng song song với AB cắt BI tại E và cắt BD tại F,Chứng minh rằng:
Lời giải
a. Ta có cân tại M 
Do MI // BC 
b. Có BD là phân giác ngoài của 
c. Có: 
d. Hướng dẫn
Lời giải: 
+) 
+)	+) 
Từ (1)(2)(3)(4) 
C. CÁC TRƯỜNG HỢP ĐỒNG DẠNG CỦA TAM GIÁC
1. Trường hợp đồng dạng thứ nhất: Nếu ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia thì hai tam giác đó đồng dạng
2. Trường hợp đồng dạng thứ hai: Nếu hai cạnh của tam giác này tỷ lệ với hai cạnh của tam giác kia và hai góc tạo bởi các cặp cạnh đó bằng nhau, thì hai tam giác đó đồng dạng với nhau
3. Trường hợp đồng dạng thứ ba: Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng
Bài 1: Cho tam giác ABC và điểm O thuộc miền trong tam giác. Qua điểm O vẽ các đường thẳng song song với Ca, CB, AB chúng lần lượt cắt các cạnh AB, BC, CA tại D, E, F. Chứng minh rằng:
Lời giải
+) 
+) Tứ giác OFCN là hình bình hành 
+) 
Từ (1)(2)(3) 
Bài 2: Cho hai tam giác đều ABC và DEF có điểm F thuộc đoạn BC, điểm A thuộc đoạn DE, B và E cùng phía so với đường thẳng AF. Chứng minh rằng: CD // BE
Lời giải
- Chứng minh tương tự: 
Bài 3: Cho tam giác ABC cân tại A, M là trung điểm của BC. Các điểm D và E thay đổi lần lượt thuộc các cạnh AB, AC sao cho Chứng minh rằng khoảng cách từ M đến DE không đổi 
Lời giải
Phân tích:
- Khoảng cách từ M đến DE bằng MH
Ta đi chứng minh: là phân giác 
Giải:
Ta có: 
 là phân giác của 
- Gọi K là hình chiếu của M trên AB suy ra K cố định do M cố định ( cố định ) 
Bài 4: Trên đường thẳng d lấy bốn điểm A, B, C, D theo thứ tự ấy sao cho: Từ điểm M nằm ngoài đường thẳng d sao cho Nối M với A, B, C, D. Qua C kẻ đường thẳng a song song với MA, đường thẳng a cắt tia MB, MD lần lượt tại I và K
a. Biết MB = 6cm, MD = 8cm. Tính BD
b. Tính chu vi tam giác ADM biết chu vi tam giác ADM bằng chu vi tam giác KCD cộng thêm 6cm
c. Chứng minh rằng C là trung điểm của IK 
Lời giải
a. là phân giác 
- Lại có: là phân giác góc ngoài của ( hai tia phân giác của hai góc kề bù ) vuông tại M 
b. Xét có 
c. C là trung điểm của IK 
Bài 5: Cho hình chữ nhật ABCD, kẻ . Gọi M, N, K lần lượt là trung điểm của BC, AH, DH
a. Tứ giác MNKC là hình gì?
b. Chứng minh rằng: 
c. Chứng minh rằng: 
Lời giải
a. là hình bình hành 
b. Hướng dẫn câu b
 ( dựa vào đồng dạng tam giác vuông 
giải: Xét có: 
Xét 
Lại có: ( hai góc tương ứng ) 
c. 
Cách khác: Chứng minh K là trực tâm 
Bài 6: Cho tam giác ABC vuông tại A, AB < AC, là phân giác 
a. Chứng minh rằng: 
b. 
c. Biết chu vi tam giác ABC là 24cm, chu vi tam giác AHC là 12cm, chu vi tam giác AHB là 9cm. Tính các cạnh của tam giác ABC
Lời giải
a. 
b. 
c. 
Xét 
CÁC BÀI TOÁN TRONG ĐỀ THI LIÊN QUAN ĐẾN TAM GIÁC ĐỒNG DẠNG
Bài 1: Cho tam giác ABC vuông tại A ( AC > AB), đường cao AH ( H thuộc BC). Trên tia HC lấy điểm D sao cho HD = HA. Đường vuông góc với BC tại D cắt AC tại E
a. Chứng minh rằng: , tính độ dài đoạn BE theo AB = m
b. Gọi M là trung điểm của BE. Chứng minh rằng . Tính 
c. Tia AM cắt BC tại G. Chứng minh rằng: 
Lời giải
a. có:
Cần thêm: 
Vậy 
+) vuông cân theo giả thiết vuông cân tại A
b. có: 
Cần thêm: 
- Ta có: 
+) vuông cân tại H 
Vậy 
c. Ta có: vuông cân tại A nên AM là phân giác 
mà: 
Vậy: 
Bài 2: Cho tam giác ABC có ba góc nhọn, các đường cao AD, BE, CF cắt nhau tại H
a. Chứng minh rằng: 
b. 
c. Chứng minh H là giao điểm các đường phân giác của tam giác DEF
d. Gọi M, N, P, Q, J, K lần lượt là trung điểm của BC, CA, AB, EF, FD, DE. Chứng minh rằng ba đường thẳng MQ, NI, PK đồng quy tại 1 điểm
Bài 3: Cho hình chữ nhật ABCD. Trên đường chéo BD lấy điểm P. Gọi M là điểm đối xứng của điểm C qua P
a. Tứ giác AMDB là hình gì?
b. Gọi E và F lần lượt là hình chiếu của điểm M lên AB. Chứng minh rằng EF // AC và ba điểm E, F, P thẳng hàng
c. Chứng minh rằng tỷ số các cạnh của hình chữ nhật MEAF không phụ thuộc vào vị trí của điểm P
d. Giả sử CP vuông góc với BD và CP = 2,4 cm, tính các cạnh của hình chữ nhật biết: 
Bài 4: [ Việt yên – Bắc Giang – 30/04/2013 ]. Cho hình vuông ABCD, trên cạnh AB lấy điểm E và trên cạnh AD lấy điểm F sao cho AE = AF. Vẽ AH cắt DC và BC tại M, N
a. Chứng minh rằng tứ giác AEMD là hình chữ nhật
b. Biết Chứng minh rằng: AC = 2.EF c. Chứng minh rằng: 
Lời giải
1
(2.0 điểm)
Ta có (cùng phụ )
 AB = AD ( gt) 
 (ABCD là hình vuông) 
 (g.c.g) 
 => DM=AF, mà AF = AE (gt) 
 Nên. AE = DM 
 Lại có AE // DM ( vì AB // DC )
Suy ra tứ giác AEMD là hình bình hành
Mặt khác. (gt) 
Vậy tứ giác AEMD là hình chữ nhật
2
(2.0 điểm)
Ta có (g.g) 
 hay ( AB=BC, AE=AF) 
Lại có (cùng phụ )
 (c.g.c)
, mà (gt) nên BC2 = (2AE)2
 BC = 2AE E là trung điểm của AB, F là trung điểm của AD 
Do đó: BD = 2EF hay AC = 2EF (đpcm)
3
(2.0 điểm)
Do AD // CN (gt). Áp dụng hệ quả định lý ta lét, ta có: 
Lại có: MC // AB ( gt). Áp dụng hệ quả định lý ta lét, ta có:
 hay 
 (Pytago) 
 (đpcm)
Bài 5: [ Yên Phong – 20/03/2018 ]. Cho hình vuông ABCD, trên tia đối cả tia CD lấy điểm M bất kỳ ( CM < CD), vẽ hình vuông CMNP ( P nằm giữa B và C), DP cắt BM tại H, MP cắt BD tại K
a. Chứng minh rằng: 
b. Tính 
c. Chứng minh rằng: 
Bài 6: [ Yên Phong – 2015 - 2016 ]. Cho tam giác ABC vuông tại A, đường cao AH. Gọi E, F theo thứ tự là hình chiếu của H trên AC và AB. Cho D là 1 điểm trên BC. Gọi M, N theo thứ tự là hình chiếu của D trên AB và AC. Chứng minh rằng
a. 
b. 
c. 
Bài 7: [ Chương Mỹ, 2018 - 2019 ].
Cho ∆ABC có , AB < AC, đường cao AH. Gọi M, N lần lượt là hình chiếu của H trên cạnh AB và AC.
a. Chứng minh rằng: MN = AH
b. Chứng minh rằng: AM.AB = AN.AC = AH2
c. Gọi K là giao điểm của NM và BC. Chứng minh rằng: KB.KC = KH2;
d. Gọi O là trung điểm của BC, I là giao điểm của MN và AH. Chứng minh rằng OI vuông góc với AK.
e. Giả sử . Tính tỉ số 
a)
2đ
HM ⊥ AB tại M (vì M là hình chiếu của H trên AB)
HN ⊥ AC tại N (N là hình chiếu của H trên AC)
Xét tứ giác AMHN có 
AMHN là hình chữ nhật
AH = MN (t/c hình chữ nhật)
b)
2đ
Ta có AMHN là hình chữ nhật (CMT)
(t/c hình chữ nhật)
Mà (cùng phụ với góc HAB)
 hay 
Xét ∆ANM và ∆ABC có
Góc A chung, 
∆ANM đồng dạng với ∆ABC (góc – góc)
AM.AB = AN.AC
Chứng minh được: AM.AB = AH2
c)
1đ
Chứng minh ∆KHM đồng dạng với ∆KNH (góc K chung, góc KHM = góc KNH cùng bằng góc HAB)
 (1)
Chứng minh ∆KMB đồng dạng với ∆KCN (góc K chung, góc KMB bằng góc C cùng bằng góc AMN)
KM.KN = KB.KC (2)
Từ (1) và (2) => KH2 = KB.KC
d)
1đ
∆ABC vuông tại A, trung tuyến AO
AO = OB = OC (t/c trung tuyến ∆ vuông)
∆OAC cân tại O =>(T/c ∆ cân)
Mà (∆ANM đồng dạng với ∆ABC)
Mà 
 => OA ⊥ MN hay OA ⊥ KN
Xét ∆KAO
Có AH ⊥ KO, KN ⊥ OA mà AH cắt KN tại I => I là trực tâm ∆KAO => OI ⊥ AK
e)
1đ
AH = 40t, AO = 41t
Xét ∆HAO vuông tại H ta có:
OA2 = OH2 + AH2 (đli Pitago)
OH2 = OA2 – AH2 = (41t)2 – (40t)2 = 81t2
OH = 9t
Mà OA = OB = OC (t/c trung tuyến ∆ vuông ABC)
OC = 41t => HC = 41t + 9t = 50t
Chứng minh: ∆HAC đồng dạng với ∆ABC (g.g)
Bài 8: [ Vĩnh Lộc, 2016 - 2017 ].
Cho tam giác ABC phân giác AD. Trên nửa phẳng không chứa A bờ BC, vẽ tia Cx sao cho = . Cx cắt AD tại E ; I là trung điểm DE. Chứng minh rằng :
a. đồng dạng với b. AE2 > AB.AC
c. 4AB.AC = 4AI2 – DE2 d. Trung trực của BC đi qua E
Lời giải
a) Xét ABD và CED có:
 (đối đỉnh)=> ABD CED (g -g)
b) Xét ABD và AEC có:
 (ABD = CED)
=> ABD AEC (g-g)
=> => AB.AC = AD.AE < AE2 (AD < AE)
Vậy AE2 > AB.AC
c) Ta có: 4AI2 - DE2 = 4AI2 - 4DI2 = 4(AI - DI)(AI +DI) = 4AD(AI + IE) = 4AD.AE 
Mà AD.AE = AB.AC (câu b) => 4AB.AC = 4AI2 - DE2
d) Chứng minh trung trực của BC qua E.
+) ABE ADC
 ; ( AD.AE = AB.AC) => ABE ADC (c.g.c) => 
+ ) BDE; ADC
 (đối đỉnh)
=> BDE ADC (g-g) => => BEC cân tại E 
=> Trung trực BC qua E
Bài 9: [ Cẩm Thủy, 2013 - 2014 ].
Cho hình vuông ABCD có AC cắt BD tại O. M là điểm bất kỳ thuộc cạnh BC 
(M khác B, C).Tia AM cắt đường thẳng CD tại N . Trên cạnh AB lấy điểm E sao cho BE = CM.
a. Chứng minh : ∆OEM vuông cân. 
b. Chứng minh : ME // BN.
c. Từ C kẻ CH BN ( H BN). Chứng minh rằng ba điểm O, M, H thẳng hàng.
Lời giải
a
3
đ
Xét ∆OEB và ∆OMC
Vì ABCD là hình vuông nên ta có OB = OC 
 Và 
 BE = CM ( gt )
Suy ra ∆OEB = ∆OMC ( c .g.c)	
 OE = OM và 
Lại có vì tứ giác ABCD là hình vuông
 kết hợp với OE = OM ∆OEM vuông cân tại O
b
2đ
Từ (gt) tứ giác ABCD là hình vuông AB = CD và AB // CD
+ AB // CD AB // CN ( Theo ĐL Ta- lét) (*)
Mà BE = CM (gt) và AB = CD AE = BM thay vào (*)
Ta có : ME // BN ( theo ĐL đảo của đl Ta-lét)
c
1đ
Gọi H’ là giao điểm của OM và BN
Từ ME // BN ( cặp góc so le trong)
Mà vì ∆OEM vuông cân tại O
∆OMC ∆BMH’ (g.g)
 ,kết hợp ( hai góc đối đỉnh)
∆OMB ∆CMH’ (c.g.c) 
Vậy 
Mà CH BN ( H BN) H H’ hay 3 điểm O, M, H thẳng hàng ( đpcm)
Bài 10: [ Duy Tiên, 2012 - 2013 ].
Cho hình vuông ABCD cạnh a, điểm E thuộc cạnh BC, điểm F thuộc cạnh AD sao cho CE=AF. Các đường thẳng AE, BF cắt đường thẳng CD theo thứ tự tại M, N.
a) Chứng minh rằng: CM.DN = a2
b) Gọi K là giao điểm của NA và MB. Chứng minh rằng: 
c) Các điểm E và F có vị trí như thế nào thì MN có độ dài nhỏ nhất?
Lời giải
a) Vì ABCD là hình vuông 
Vì AB//CM 
Vì AB//DN 
Từ (1)(2)(3) 
b) Theo câu a, ta có: 
Do đó 
Mà 
Từ (4)(5) 
Do đó 
c) Áp dụng BĐT côsi ta có
Dấu "=" xảy ra khi DN = CM = a. Khi đó 
hay 
Vậy khi E và F lần lượt là trung điểm của BC và AD thì MN có độ dài nhỏ nhất là 3a
Bài 11: [ Gia Viễn, 2014 - 2015 ].
Câu 4. (6,5 điểm) Cho hình vuông ABCD, trên tia đối của tia CD lấy điểm M bất kì (CM < CD), vẽ hình vuông CMNP (P nằm giữa B và C), DP cắt BM tại H, MP cắt BD tại K. 
a) Chứng minh: DH vuông góc với BM. 
b) Tính Q = 
c) Chứng minh: MP . MK + DK . BD = DM2
Lời giải
(2,25 điểm) Chứng minh: DH vuông góc với BM
- HS CM : CD = BC, PC = CM, DCB = BCM = 900
- CM: D DPC = D BMC (cgc)
- Chứng minh được BHP = 900 
(2,0 điểm) Tính Q = 
- CM : MP ^ BD 
- ; 
Tương tự : 
Þ Q = 
c) (2,0 điểm) Chứng minh: MP . MK + DK . BD = DM2
- CM: D MCP ~ DMKD (g.g) 
 Þ MP . MK = MC . MD (1)
- CM: DDBC ~ DDKM (g.g) 
 Þ DK . BD = DC. DM (2) 
- Từ (1) và (2) Þ MP . MK + DK . BD = DM .(MC + DC)
 Þ MP . MK + DK . BD = DM2