Đề kiểm tra học kỳ II môn Toán 7 - Trường THCS Quách Xuân Kỳ

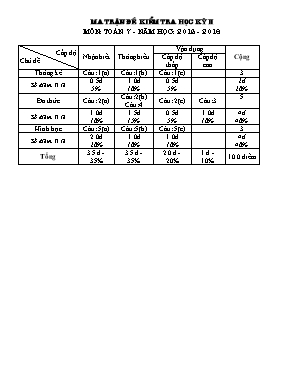
Ma trËn ®Ò kiÓm tra häc kú ii
M«n: to¸n 7 - N¨m häc: 2015 - 2016
 Cấp độ
Chủ đề
Nhận biết
Thông hiểu
Vận dụng
Cộng
Cấp độ thấp
Cấp độ cao
Thống kê
Câu: 1(a)
Câu: 1(b)
Câu: 1(c)
3
Số điểm, Tỉ lệ
0.5đ 
5%
1.0đ 
10%
0.5đ 
5%
2đ
20%
Đa thức
Câu: 2(a)
Câu: 2(b)
Câu: 4
Câu: 2(c)
Câu: 3
5
Số điểm, Tỉ lệ
1.0đ 
10%
1.5đ 
15%
0.5đ 
5%
1.0đ 
10%
4đ
40%
Hình học
Câu: 5(a)
Câu: 5(b)
Câu: 5(c)
3
Số điểm, Tỉ lệ
2.0đ 
20%
1.0đ 
10%
1.0đ 
10%
4đ
40%
Tổng
3.5 đ - 35%
3.5 đ -
35%
2.0 đ - 
20%
1 đ - 
10%
10.0 điểm
Tr­êng thcs qu¸ch xu©n kú
®Ò kiÓm tra häc kú II
m«n to¸n 7 - N¡M HäC: 2015 - 2016
M· ®Ò 02 - §Ò Ch½n - Thêi gian lµm bµi: 90 phót
§Ò bµi
C©u 1: (2.0 ®). Một xạ thủ thi bắn súng. Điểm số đạt được sau mỗi lần bắn được
 ghi vào bảng sau 
10
9
10
9
9
9
8
9
9
10
9
10
10
7
8
10
8
9
8
9
9
8
10
8
8
9
7
9
10
9
 a/ Dấu hiệu ở đây là gì ? có bao nhiêu giá trị của dấu hiệu.
 b/ Lập bảng tần số. Nêu nhận xét.
 c/ Tính số trung bình cộng của dấu hiệu.
C©u 2: (2.0®). 	Cho hai đa thức:
	P(x) = 11 – 2x3 + 4x4 + 5x – x4 – 2x
	Q(x) = 2x4 – x + 4 – x3 + 3x – 5x4 + 3x3
	a/ Thu gọn và sắp xếp các đa thức trên theo lũy thừa giảm của biến.
	b/ Tính P(x) + Q(x)
	c/ Tìm nghiệm của đa thức H(x) = P(x) + Q(x)
C©u 3: (1.0®). Tìm m để x = - 1 là nghiệm của đa thức P(x) = x + 2x + m – 1	
C©u 4: (1.0®).) Cho hai đa thức : A = ; B = 
 	Tính : A – B 
C©u 5: (4.0®). Cho ABC cân tại A, kẻ AHBC. Biết AB = 5cm, BC = 6cm
Tính độ dài các đoạn thẳng BH, AH?
Gọi G là trọng tâm của tam giác ABC. Chứng minh rằng ba điểm A, G, H thẳng hàng?
Chứng minh: góc ABG = góc ACG
BiÓu ®iÓm vµ h­íng dÉn chÊm
m«n to¸n 7 - N¡M HäC: 2015 - 2016
M· ®Ò 02 - Đề Chẵn
C©u
§¸p ¸n
§iÓm
C©u 1:
(2.0 ®)
a/ Dấu hiệu ở đây là điểm số đạt được của một xạ thủ sau mỗi lần bắn súng. Có 30 giá trị 
b/ Bảng tần số 
Điểm số x
7
8
9
10
Tần số (n) 
2
7
13
8
N = 30
Xạ thủ đã bắn 30 phát súng 
Điểm số cao nhất là 10; điểm số thấp nhất là 7 
Điểm số xạ thủ bắn đạt nhiều nhất là 9 có tần số là 13 
Điểm số xạ thủ bắn đạt thấp nhất là 7 có tần số là 2
c/ Số trung bình của dấu hiệu 
 X = 
0.25đ
0.25đ
0.25đ
0.25đ
0.25đ
0.25đ
0.5đ
C©u 2:
(2.0 ®)
a) P(x) = 11 – 2x3 + 4x4 + 5x – x4 – 2x 
 = 4x4 – x4 – 2x3 + 5x – 2x +11
 = 3x4– 2x3 + 3x +11
 Q(x) = 2x4 – x + 4 – x3 + 3x – 5x4 + 3x3 
 = 2x4 – 5x4 – x3 + 3x3 – x + 3x + 4
 = – 3x4 + 2x3 + 2x + 4
0.25đ
0.25đ
0.25đ
0.25đ
b) P(x) = 3x4– 2x3 + 3x + 11
 Q(x) = – 3x4 + 2x3 + 2x + 4 
 P(x) + Q(x) = 5x + 15
0.5đ
c) Có : H(x) = P(x) + Q(x) = 5x + 15
	H(x) có nghiệm khi H(x) = 0
	=> 5x + 15 = 0 => x = - 3
	Vậy nghiệm của H(x) là x = -3 
0.5đ
C©u 3:
(1.0 ®)
Tìm m để x = - 1 là nghiệm của đa thức P(x) = x + 2x + m – 1 
Giải: Thay x = -1 vào đa thức P(x) ta có
P(-1) = ( - 1 ) + 2.(-1) + m – 1 = 0 
 1 – 2 + m – 1 = 0 
 m – 2 = 0 
 m = 2 
Vậy với m = 2 thì đa thức P(x) = x + 2x + m – 1 
 có nghiệm x = - 1
0.25đ
0.25đ
0.25đ
0.25đ
C©u 4:
(1.0 ®)
A – B = ( 7a – 4ab – b ) – ( 2a – ab + b ) 
 = 7a – 4ab – b – 2a + ab – b 
 = 5a – 3ab – 2b 
0.5đ
0.5đ
C©u 5:
(4.0 ®)
Viết được GT, KL và vẻ hình đúng.
a) Xét ∆ABC cân tại A có AH là đường cao nên AH cũng là trung tuyến 
 BH = HC = = 6 : 2 = 3 (cm)
Áp dụng định lí Pitago vào tam giác vuông AHB,
 Ta có AB2 = BH2 +AH2 
 52 = 32 + AH2 
 Þ AH2 = 52 – 32 = 25 – 9 = 16 
 Þ AH = 4cm
0.5đ
0.5đ
0.5đ
0.5đ
b) Ta có BH = HC (Theo cm trên). 
 Vậy AH là trung tuyến tuyến của tam giác ABC 
 Mà G là trọng tâm của tam giác nên G AH . 
 Vậy A; G; H thẳng hàng (đpcm)
0.5đ
0.5đ
c) Xét ∆ABG và ∆ACG
 Có AB = AC (gt)
 BAG = GAC (∆ABH = ∆ACH) 
 AG cạnh chung 
 Vậy ∆ABG = ∆ACG (c.g.c) 
 Þ ABG = ACG
0.5đ
0.5đ
Tr­êng thcs qu¸ch xu©n kú
®Ò kiÓm tra häc kú II
m«n to¸n 7 - N¡M HäC: 2015 - 2016
M· ®Ò 02 - Đề Lẽ - Thêi gian lµm bµi: 90 phót
§Ò bµi
C©u 1: (2.0 ®). Một xạ thủ thi bắn súng. Điểm số đạt được sau mỗi lần bắn được
 ghi vào bảng sau 
10
9
10
9
9
9
8
8
9
8
8
10
8
7
8
10
8
9
8
9
9
8
10
8
8
9
7
7
10
9
 a/ Dấu hiệu ở đây là gì ? có bao nhiêu giá trị của dấu hiệu.
 b/ Lập bảng tần số. Nêu nhận xét.
 c/ Tính số trung bình cộng của dấu hiệu.
C©u 2: (2.0®). 	f(x) = 
 h(x) = 
a) Sắp xếp các đa thức trên theo lũy thừa giảm của biến
a) Tính Q(x) = f(x) + h(x)
b) Tìm nghiệm Q(x) 
C©u 3: (1.0®). Tìm m để x = - 1 là nghiệm của đa thức P(x) = x + 2x + m – 1	
C©u 4: (1.0®).) Cho hai đa thức : A = ; B = 
 	Tính : A + B
C©u 5: (4.0®). Cho MNQ cân tại M, kẻ MINQ. Biết MN = 5cm, NQ = 6cm
Tính độ dài các đoạn thẳng NI, MI?
Gọi G là trọng tâm của tam giác MNQ. Chứng minh rằng ba điểm M, G, I thẳng hàng?
Chứng minh: góc MNG = góc MQG
BiÓu ®iÓm vµ h­íng dÉn chÊm
m«n to¸n 7 - N¡M HäC: 2015 - 2016
M· ®Ò 02 - Đề Lẽ
C©u
§¸p ¸n
§iÓm
C©u 1:
(2.0 ®)
a/ Dấu hiệu ở đây là điểm số đạt được của một xạ thủ sau mỗi lần bắn súng. Có 30 giá trị 
b/ Bảng tần số 
Điểm số x
7
8
9
10
Tần số (n) 
3
11
10
6
N = 30
Xạ thủ đã bắn 30 phát súng 
Điểm số cao nhất là 10; điểm số thấp nhất là 7 
Điểm số xạ thủ bắn đạt nhiều nhất là 8 có tần số là 11 
Điểm số xạ thủ bắn đạt thấp nhất là 7 có tần số là 3
c/ Số trung bình của dấu hiệu 
 X = 
0.25đ
0.25đ
0.25đ
0.25đ
0.25đ
0.25đ
0.5đ
C©u 2:
(2.0 ®)
a) f(x) = 
 = 3x4 + x3 + 4x2 - 3
 h(x) = 
 = 3x4 + x3 +10x2 - 5x - 3
0.25đ
0.25đ
0.25đ
0.25đ
b) f(x) = 3x4 + x3 + 4x2 - 3
 h(x) = 3x4 + x3 + 10x2 - 5x - 3
 f(x) - h(x) = - 6x2 + 5x
0.5đ
c) Có : Q(x) = f(x) - h(x) = - 6x2 + 5x
	Q(x) có nghiệm khi Q(x) = 0
	=> - 6x2 + 5x= 0 => x = 0 hoặc x = 
	Vậy Q(x) có hai nghiệm là x = 0 hoặc x = 
0.5đ
C©u 3:
(1.0 ®)
Tìm m để x = - 1 là nghiệm của đa thức P(x) = x + 2x + m – 1 
Giải: Thay x = -1 vào đa thức P(x) ta có
P(-1) = ( - 1 ) + 2.(-1) + m – 1 = 0 
 1 – 2 + m – 1 = 0 
 m – 2 = 0 
 m = 2 
Vậy với m = 2 thì đa thức P(x) = x + 2x + m – 1 
 có nghiệm x = - 1
0.25đ
0.25đ
0.25đ
0.25đ
C©u 4:
(1.0 ®)
A + B = ( 7a – 4ab – b ) + ( 2a – ab + b )
 = 7a – 4ab – b + 2a – ab + b 
 = 9a – 5ab 
0.5đ
0.5đ
C©u 5:
(4.0 ®)
Viết được GT, KL và vẻ hình đúng.
a) Xét ∆MNQ cân tại M có MI là đường cao nên MI cũng là trung tuyến 
 NI = IQ = = 6 : 2 = 3 (cm)
Áp dụng định lí Pitago vào tam giác vuông MIN
 Ta có MN2 = NI2 +MI2 
 52 = 32 + MI2 
 Þ MI2 = 52 – 32 = 25 – 9 = 16 
 Þ MI = 4cm
0.5đ
0.5đ
0.5đ
0.5đ
b) Ta có NI = IQ (Theo cm trên). 
 Vậy MI là trung tuyến tuyến của tam giác MNQ 
 Mà G là trọng tâm của tam giác nên G MI . 
 Vậy M, G, I thẳng hàng (đpcm)
0.5đ
0.5đ
c) Xét ∆MNG và ∆MQG
 Có MN = MQ (gt)
 NMG = QMG (∆MNI = ∆MQI) 
 MG cạnh chung 
 Vậy ∆MNG = ∆MQG (c.g.c) 
 Þ MNG = MQG
0.5đ
0.5đ