Đề kiểm tra học kì II năm học 2015-2016 môn Toán lớp 9 Trường THCS-THPT Hồng Hà

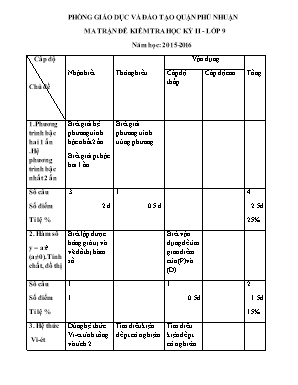
 PHÒNG GIÁO DỤC VÀ ĐÀO TẠO QUẬN PHÚ NHUẬN
 MA TRẬN ĐỀ KIỂM TRA HỌC KỲ II - LỚP 9
 Năm học: 2015-2016
 Cấp độ
Chủ đề
Nhận biết
Thông hiểu
 Vận dụng
Tổng
Cấp độ thấp
Cấp độ cao
1.Phương trình bậc hai 1 ẩn .Hệ phương trình bậc nhất 2 ẩn
Biết giải hệ phương trình bậc nhất 2 ẩn
Biết giải pt bậc hai 1 ần
Biết giải phương trình trùng phương 
Số câu
Số điểm
Tỉ lệ %
 3
 2 đ 
1
 0.5 đ 
4
 2.5đ
25%
2. Hàm số
y = ax2 (a≠0). Tính chất, đồ thị
Biết lập được bảng giá trị và vẽ đồ thị hàm số 
Biết vận dụng để tìm giao điểm của (P)và (D)
Số câu 
Số điểm 
Tỉ lệ %
1
1
1
0.5đ
2
1.5đ
15%
3. Hệ thức
Vi-ét
và ứng dụng
Dùng hệ thức Vi-et tính tổng và tích 2 nghiệm
Tìm điều kiện để pt có nghiệm
Tìm điều kiện để pt có nghiêm thỏa mãn đk
Số câu
Số điểm
Tỉ lệ %
1
 0.5đ
1
 0.5đ
1
 0.5đ
3
 1,5đ
15%
4.Lãi suất 
Biết thiết lập công thức và tính lãi suất 
Số câu 
Số điểm
Tỉ lệ %
1
1đ
1
1đ
10%
5.Tam giác đồng dạng .Góc với đường tròn
Nhận biết tam giác đồng dạng 
Nhận biết tứ giác nội tiếp
-Chứng minh tứ giác nội tiếp
-Hiểu được tính chất cũa tứ giác nội tiếp để chứng minh 
Biết vận dụng tính chất của góc để chứng minh ba điểm thẳng hàng 
Số câu
Số điểm
Tỉ lệ %
2
 2
1
 1
1
 0.5đ
4
 3,5đ
35%
T. số câu
T. số điểm
Tỉ lệ %
 7 
 5,5đ
 55% 
 4 
 3đ
 30%
2
 1 đ
 10%
1
 0.5đ
 5% 
14
 10đ
100% 
ĐỀ ĐỀ NGHỊ : TRƯỜNG THCS-THPT HỒNG HÀ 
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO QUẬN PHÚ NHUẬN
ĐỀ KIỂM TRA HỌC KÌ II NĂM HỌC 2015-2016
MÔN TOÁN LỚP 9
Thời gian làm bài :90phút (không kể thời gian phát đề )
Bài 1:(2,5 điểm ).Giải các phương trình và hệ phương trình sau :
a)14x2 -7x=0 b)3x2 -8x -3=0 c) x4 – 3x2 – 4 = 0 d) 5x+4y=-33x+2y=11
Bài 2: (1,5điểm)Cho Parabol (P):y=x2 và đường thẳng (D):y=x +2
a)Vẽ (P) và (D)trên cùng hệ trục tọa độ
b)Tìm giao điểm của (P) và (D)bằng phép toán 
Bài 3: (1.5điểm)Cho phương trình x2 – 2mx – 1 = 0 (m là tham số)
a)Chứng minh phương trình trên luôn có 2 nghiệm phân biệt.
b)Tính tổng và tích hai nghiệm x1,x2 theo m
c) Gọi x1, x2 là hai nghiệm của phương trình trên. Tìm m để .
Bài 4:(1 điểm ) Cô Oanh gửi tiền tiết kiệm vào ngân hàng một số tiền là 50 000 000đồng với lãi suất 0,8% một tháng (lãi kép ).Hỏi sau tròn hai năm số tiền tiết kiệm trong sổ tiết kiệm của cô là bao nhiêu ( chính xác đến hàng đơn vị)
Câu 5: (3.5điểm) Từ điểm M ở ngoài đường tròn (O) vẽ cát tuyến MCD không đi qua tâm O và hai tiếp tuyến MA, MB đến đường tròn (O), ở đây A, B là các tiếp điểm và C nằm giữa M, D.
 a) Chứng minh MA2 = MC.MD.
	b) Gọi I là trung điểm của CD. Chứng minh rằng 5 điểm M, A, O, I , B cùng nằm trên một đường tròn.
	c) Gọi H là giao điểm của AB và MO. Chứng minh tứ giác CHOD nội tiếp được đường tròn
	d) Gọi K là giao điểm của các tiếp tuyến tại C và D của đường tròn (O). Chứng minh A, B, K thẳng hàng. 
 Bài 
Đáp Án
Điểm 
Bài 1
a)14x2 -7x=0 7x(2x-1)=0 x=0 hoặc x=
 b)3x2 -8x -3=0 
 =b’2 –ac=16+9 =25>0 nên phương trình (1) có hai nghiệm phân biệt là
x1 = hoặc x2 ==
c) x4 – 3x2 – 4 = 0	(2)
Đặt t = x2, t ≥ 0.
Phương trình (2) trở thành t2 – 3t – 4 = 0 Û (a – b + c = 0) 
So sánh điều kiện ta được t = 4 Û x2 = 4 Û x = ± 2.
Vậy phương trình (2) có hai nghiệm phân biệt là x = 2 hoặc x = –2
 d)5x+4y=-33x+2y=115x+4y=-3-6x-4y=-225x+4y=-3-x =-25
5.25+4y=-3x =25y =-32x =25
Vậy hệ phương trình có nghiệm là x = 25 và y = -32.
0.25đx3
0,25đ
0,25đx2
0.25đ
0,25đ
0,25đ
0,25đ
Bài 2
x
-4
-2
0
2
4
y=x2
4
1
0
1
4
Bảng giá trị của hoàm số y=x2
BảBảng giá trị của hàm số y=x +2
x
0
4
Y y=x +2
2
0
Vẽ (P) và (D) đúng 
b) b) Tìm giao điểm của (P) và (D)bằng phép toán 
Phương trình hoành độ giao điểm của (P) và (D):
 x2= x +2 x2 x -2=0 x=2 hay x= -4
*x=2y=1
*x=-4 y=4
Vậy (P) cắt( D) tại hai điểm (2;1);(-4;4)
0,25đ
0,25đ
0,25đx2
0,25đ
0,25đ
Bài 3
a) Chứng minh phương trình trên luôn có 2 nghiệm phân biệt.
 Ta có: D' = m2 + 1 > 0 với mọi m nên phương trình trên luôn có hai nghiệm phân biệt.
b)S=x1 +x2 = 2m P= x1 .x2= -1
c)Do đó S2 – 3P = 7 (2m)2 + 3 = 7 Û m2 = 1 
 m = ± 1.
Vậy m thoả yêu cầu bài toán m = ± 1.
0,25đx2
0,25đ x2
0,25đx2
Bài 4
Gọi A là tiền vốn lẫn lãi sau n tháng ta có:
Tháng 1 (n = 1): A = a + ar = a(1 + r)
Tháng 2 (n = 2): A = a(1 + r) + a(1 + r)r = a(1 + r)2
Tháng n (n = n): A = a(1 + r)n – 1 + a(1 + r)n – 1.r = a(1 + r)n
Vậy T = a(1 + r)n	(*)
Trong đó: a tiền vốn ban đầu, r lãi suất (%) hàng tháng, n số tháng, A tiền vốn lẫn lãi sau n tháng.
Vậy trong hai năm số tiền trong tiết kiệm trong sổ tiết kiệm của cô Oanh là 
T=50 000 000.(1+0.8% )24 60 537 262 đồng 
0.5đx2
0,25đx2
Bài 5
a) Xét hai tam giác MAC và MDA có:
	– Ð M chung
	– Ð MAC = Ð MDA (= ).
Suy ra DMAC đồng dạng với DMDA (g – g) 
Þ Þ MA2 = MC.MD.
b) * MA, MB là tiếp tuyến của (O) nên
 ÐMAO = Ð MBO = 900.
* I là trung điểm dây CD nên Ð MIO = 900.
Do đó: Ð MAO = Ð MBO = Ð MIO = 900
Þ 5 điểm M, A, O, I, B cùng thuộc đường tròn đường kính MO.
c) Ø Ta có MA = MB (tính chất hai tiếp tuyến cắt nhau) và OA = OB = R(O). Do đó MO là trung trực của AB Þ MO ^ AB.
Trong DMAO vuông tại A có AH là đường cao Þ MA2 = MH.MO. Mà MA2 = MC.MD (do a)) Þ MC.MD = MH.MO Þ (1).
Xét D MHC và DMDO có:
ÐM chung, kết hợp với (1) ta suy ra DMHC và DMDO đồng dạng (c–g –c)
Þ Ð MHC = Ð MDO Þ Tứ giác OHCD nội tiếp.
d) Tứ giác OCKD nội tiếp(vì Ð OCK = Ð ODK = 900)
Þ Ð OKC = Ð ODC = Ð MDO mà Ð MDO = Ð MHC (cmt)
Þ Ð OKC = Ð MHC Þ OKCH nội tiếp 
Þ Ð KHO = Ð KCO = 900.
Þ KH ^ MO tại H mà AB ^ MO tại H 
Þ HK trùng AB Þ K, A, B thẳng hàng.
0,25đ
0,25đ
0,25đx2
0,25đ
0,25đx2
0,25đ
0,25đ
0,25đ
0,25đ
0,25đ
0,25đ
0,25đ
Chú ý :
-Học sinh có cách giải khác trong phạm vi kiến thức đã học vẫn được chấm theo các phần tương tự đáp án 
-Phần hình học nếu không có hình vẽ thì không chấm cả bài 
 Giáo viên ra đề và lập đáp án 
 Bùi Viết Hoàng