Đề kiểm tra học kì II môn toán lớp 8 năm học 2013 - 2014

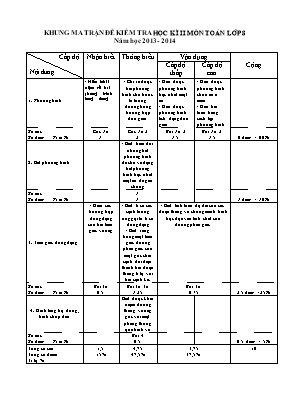
KHUNG MA TRẬN ĐỀ KIỂM TRA HOÏC KÌ II MOÂN TOAÙN LÔÙP 8
Năm học 2013 - 2014
 Cấp độ
 Nội dung
Nhận biết
Thông hiểu
Vận dụng
Cộng
Cấp độ thấp
Cấp độ cao
1. Phương trình
- HiÓu kh¸i niÖm vÒ hai ph­¬ng tr×nh t­¬ng ®­¬ng
- Chỉ ra được hai phương trình cho trước là tương đương trong trường hợp đơn giản
- Giải được phương trình bậc nhất một ẩn
- Giải được phương trình tích dạng đơn giản
- Giải được phương trình chứa ẩn ở mẫu
- Giải bài toán bằng cách lập phương trình
Số câu 
Số điểm Tỉ lệ %
Câu 1a
1
Câu 1b,2
2
Bài 1a, 2 
1,5
Bài 1b, 2
1,5
6 điểm = 60% 
2. Bất phương trình
- Biết biến đổi những bất phương trình đã cho về dạng bất phương trình bậc nhất một ẩn để giải chúng
Số câu 
Số điểm Tỉ lệ %
1
1
1 điểm = 10% 
3. Tam giác đồng dạng
- Hiểu các trường hợp đồng dạng của hai tam giác vuông
- Biết tỉ số các cạnh tương ứng gọi là tỉ số đồng dạng
- Biết rằng trong một tam giác đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề.
- Biết tính toán độ dài của các đoạn thẳng và chứng minh hình học dựa vào tính chất của đường phân giác
Số câu 
Số điểm Tỉ lệ %
Bài 3a
0,5
Bài 3a, 3b
1,25
Bài 3b
0,75
2,5 điểm =25%
4. Hình lăng trụ đứng, hình chóp đều
Biết được khái niệm đường thẳng vuông góc với mặt phẳng thông qua hình vẽ
Số câu 
Số điểm Tỉ lệ %
Bài 4
0,5
0,5 điểm = 5% 
Tổng số câu 
Tổng số điểm
Tỉ lệ %
1,5
15%
4,75
47,5%
3,75
37,5%
10
 PHÒNG GD&ĐT ĐẠI LỘC	 ĐỀ THI HKII
TRƯỜNG THCS NGUYỄN HUỆ MÔN TOÁN 8
A. LÝ THUYẾT: (2 ñieåm). 
Học sinh chọn một trong hai câu sau:
Câu 1: 
a) Thế nào là hai phương trình tương đương?
b) Xét xem cặp phương trình sau có tương đương với nhau không? Giải thích.
2x – 4 = 0 (1) và (x – 2)(x2 + 1) = 0 (2)
Câu 2:
a) Phát biểu định nghĩa hai tam giác đồng dạng.
b) Áp dụng: Cho A’B’C’~ABC, biết A’B’ = 4cm; A’C’ = 6cm; A = 8cm; BC = 16cm. Tính AC; B’C’.
B. BÀI TOÁN BẮT BUỘC: (8 ñieåm).
Bài 1: (3 điểm) Giải các phương trình và bất phương trình sau đây:
(x + 1)(2x – 1) = 0
Bài 2: (2 điểm) Giải bài toán bằng cách lập phương trình.
Một người khởi hành từ A lúc 7 giờ sáng và dự định tới B lúc 11 giờ 30 phút cùng ngày. Do đường chưa tốt, nên người ấy đã đi với vận tốc chậm hơn dự định 5 km/h. Vì thế phải 12 giờ người ấy mới đến B. Tính quãng đường AB. 
Bài 3: (2,5 điểm)
Cho tam giác ABC vuông tại A với AB = 3cm; AC = 4cm; vẽ đường cao AE.
a) Chứng minh ABC đồng dạng với EBA từ đó suy ra AB2 = BE.BC
b) Phân giác góc ABC cắt AC tại F. Tính độ dài BF.	
Baøi 4: (0,5 ®iÓm) Cho h×nh chãp tam 
gi¸c ®Òu S. ABC, gäi M lµ trung ®iÓm
cña BC (Hình veõ). 
Chøng minh r»ng: 
HƯỚNG DẪN CHẤM BÀI KIỂM TRA HỌC KỲ II MÔN TOÁN KHỐI 8
NĂM HỌC: 2013 – 2014
Nội dung
Điểm
A. LÝ THUYẾT: (2 điểm) Học sinh chọn một trong hai câu sau:
Câu 1: 
a) Hai phương trình tương là hai phương trình có cùng một tập nghiệm
b) Phương trình (1) và (2) tương đương vì có cùng một tập nghiệm S1 = S2 = {2} 
1
1
Câu 2:
a) Tam giác A’B’C’ gọi là đồng dạng với tam giác ABC nếu:
b) Áp dụng: 
A’B’C’ ~ ABC
Hay 
Suy ra cm
cm	
Vậy AC = 12cm; B’C’ = 8cm.
0,5
0,5
0,25
0,25
0,25
0,25
B (8 điểm).
Bài 1:
a) (x + 1)(2x – 1) = 0
x + 1 = 0 hoặc 2x – 1 = 0 	
1) x + 1 = 0 x = -1	
2) 2x – 1 = 0 x = 	
Vậy 	
b) 	(1)
ĐKXĐ x -1 và x 0	
 (1) x(x + 3) + (x + 1)(x – 2) = 2x(x + 1)
 x2 + 3x + x2 – 2x + x – 2 = 2x2 + 2x
 0.x = 2 (Vơ nghiệm)	. Vậy S = 
c) 
x-3 + 5 > 5(2x – 5)
x – 3 + 5 > 10x – 25
-3 + 5 + 25 > 10x – x
27 > 9x 3 > x hay x < 3 
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
Bài 2:
 Gọi x (km) là quảng đường AB (x > 0)
Vận tốc ô tô dự định đi là x : = (km/h)
Vận tốc thực tế ô tô đ đi là (km/h)
Vì vận tốc thực tế chậm hơn vận tốc dự định 5 km/h nên ta có phương trình:
 + 5 = 
Giải phương trình suy ra nghiệm x = 225
Vậy quảng đường AB dài 225 km
0,25
0,25
0,25
0,25
0,25
0,5
0,25
Bài 3:
a) ABC và EBA là hai tam giác vuông có góc B chung nên đồng dạng với nhau 
=> => AB2 = BE.BC
b) Ap dụng định lí Pytago vào tam giác vuông ABC ta có:
BC2 = AB2 + AC2 = 32 + 42 = 25
Vậy BC = 5
Vì BF là tia phân giác của góc B 
=> 
=> 
hay => AF = 3.4:8 = 1,5 cm
Ap dụng định lí Pytago vào tam giác vuông ABF ta có:
BF2 = AB2 + AF2 = 32 + 1,52 = 11,25
=> BF = 3,4 cm
0,5
0,5
0,25
0,25
0,25
0,25
0,25
0,25
Bài 4:
Vì ABC đều nên AM là đường trung tuyến cũng là đường cao => BC AM (1)
Vì SBC cân tại S nên SM là đường trung tuyến cũng là đường cao => BC SM (2)
Từ (1) và (2) => BC mp(SAM)
*Lưu ý: Học sinh có thể giải theo cách khác, nếu đúng vẫn cho điểm tối đa.